一种改进的对偶格基辅助MIMO信号检测算法*

2015-03-25张茜,周围,2

通信技术 2015年10期

关键词：对偶复杂度信道

张茜, 周围,2

(1.重庆邮电大学移动通信技术重庆市重点实验室，重庆 400065；2.重庆邮电大学光电工程学院，重庆 400065)

一种改进的对偶格基辅助MIMO信号检测算法*

张茜1, 周围1,2

(1.重庆邮电大学移动通信技术重庆市重点实验室，重庆 400065；2.重庆邮电大学光电工程学院，重庆 400065)

针对传统量化方法在对偶格基约减中存在较大的量化误差这一问题，提出了一种改进的对偶格基约减量化方法。该方法通过对量化误差进行降序排列，选取量化误差最大的一个元素作为候选点，更新该候选点的量化值，并生成新的候选矢量，最终选取最优的候选矢量作为输出解。通过理论分析和计算机仿真，对不同量化方法下不同检测算法的误比特性能进行了对比研究。结果表明，提出的方法能获得比传统量化方法更优的检测性能且更接近ML检测算法。

格基约减；对偶格基约减；量化误差

0 引言

在多输入多输出(Multiple-input multiple-output，MIMO)无线通信系统中，MIMO信号检测的基本方法包括：最大似然(maximum likelihood，ML)检测、迫零(zero forcing，ZF)检测和最小均方误差(minimum mean square error，MMSE)检测。其中ML检测可以达到满分集(分集阶数等于接收天线数)，且具有最优检测性能而成为最优检测算法，但其计算复杂度随着并行传输符号数以及信号星座规模的增加呈指数增长，因而在许多场合是无法实现的。ZF及MMSE检测是具有较低计算复杂度的线性检测算法，但不能达到满分集，在性能上与最优检测有很大的差距。另外，还有与线性检测算法相结合的串行干扰消除算法(serial interference cancel，SIC)，其性能与计算复杂度介于最优检测与线性检测算法之间;而格基约减算法(Lattice Reduction，LR)作为一种对信道矩阵进行预处理的算法，在与其他检测算法相结合的条件下，能有效提高检测算法的性能，且算法复杂度较低。

MIMO系统中，对于一个列正交的信道矩阵，线性检测等价于ML检测[1]。格基约减算法能够改善矩阵的奇异性，因此在无线通信中，常把LR用于信道矩阵的预处理操作，通过改善信道矩阵的奇异性提高检测的性能，从而改善系统的性能[2,3]。在格基约减算法中对偶格基约减(dual lattice basis reduction，DLR)算法与(原)格基约减(primal lattice basis reduction，PLR)算法一样可以获得满分集增益，并且对偶格基约减算法能够获得比原格基约减算法更好的性能。文献[4]用一种新方法证明了采用对偶格基约减算法可以获得最大接收分集，其分集阶数等于接收天线数，其检测性能优于原格基约减算法，因此本文是基于对偶格基约减算法进行的。在传统的对偶格基约减算法中，对滤波后的信号进行量化处理时，大多采用最为简单的舍入量化操作，因而量化误差比较大。本文通过对传统量化操作进行改进，在求解量化误差的同时对量化误差进行排序，对量化误差最大的发射符号的量化值进行重新取值，并生成新的发射矢量，最终选取具有最小欧式距离的发射矢量作为输出解，这样可以有效地降低量化误差，改善对偶格基约减算法的检测性能。

1 系统模型

考虑一个未编码MIMO系统，系统发射端天线数和接收端天线数分别为Nt和Nr，则该MIMO系统模型如图1所示：

图1 MIMO系统模型

系统接收端的信号模型可写成下式：

y=Hx+n

(1)

式中，x=[x1,x2,…,xNt]T为Nt×1维的复数传输信号矢量，H∈Nr×Nt为信道矩阵，n=[n1,n2,…,nNr]T为Nr×1维，方差为σ2的复高斯白噪声。

在MIMO系统中ZF检测与MMSE检测是两种比较简单的线性检测，两种方法均通过滤波矩阵而重构数据传输矢量，两种方法的检测结果如下：

(3)

式中，(·)†,(·)H,(·)-1,INt依次表示矩阵的Moore Penrose伪逆，厄米特共轭转置，矩阵取逆和一个Nt维的单位矩阵。

若将系统模型进行扩展，定义如下：

(4)

MMSE检测算法与ZF检测算法有相同的表示形式，利用式(4)模型，可将式(3)改写为：

(5)

2 算法描述

2.1 对偶格基约减

对于式(1)所描述的接收信号模型，第一步需要求出原始格基H的对偶格基，有Hd=(H†)H，对Hd进行格基约减，得到D=HdT=(H†)HT，从而有H=(D†)HTH，这里T为一个幺模矩阵(T中元素均为整数，且det(T)=±1或±j)，那么可将式(1)改写为格的形式，如下所示：

y=Hx+n=(D†)HTHx+n=(D†)Hs+n

(6)

这里，s=THx为格约减后等效的发射信号矢量。

需要注意的是：在采用格基约减对信道增益矩阵进行预处理之前，需要对式(1)所描述的系统模型做一定的变换，同时调制方式也仅限于BPSK，QPSK，MQAM或者MPAM等，故在格约减之前需要完成发射符号x到格点的映射，公式如下：

x′=x+β1Nt×1

(7)

(8)

(9)

(10)

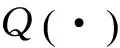
(11)

2.2 改进量化判决方法

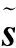
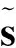
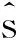
(12)

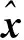
3 仿真及分析

仿真环境设定为收发天线数均为4的MIMO系统，调制方式为QPSK调制，信道为独立的平坦瑞利衰落信道。仿真结果如图2所示，图2给出了基于ZF、MMSE的DLR辅助检测算法和ML检测算法，ZF-propose、MMSE-proposed为本文算法，从图中可以看出在误符号率为10-2时，基于本文量化方法的ZF检测只比传统的量化方法性能改善约0.3 dB；而基于本文量化方法的MMSE检测其性能比传统算法优越了0.8 dB，这是由于ZF检测未考虑噪声的影响，放大信号的同时也放大了噪声，而MMSE考虑了噪声对信号的影响，因而其性能改善更为明显。

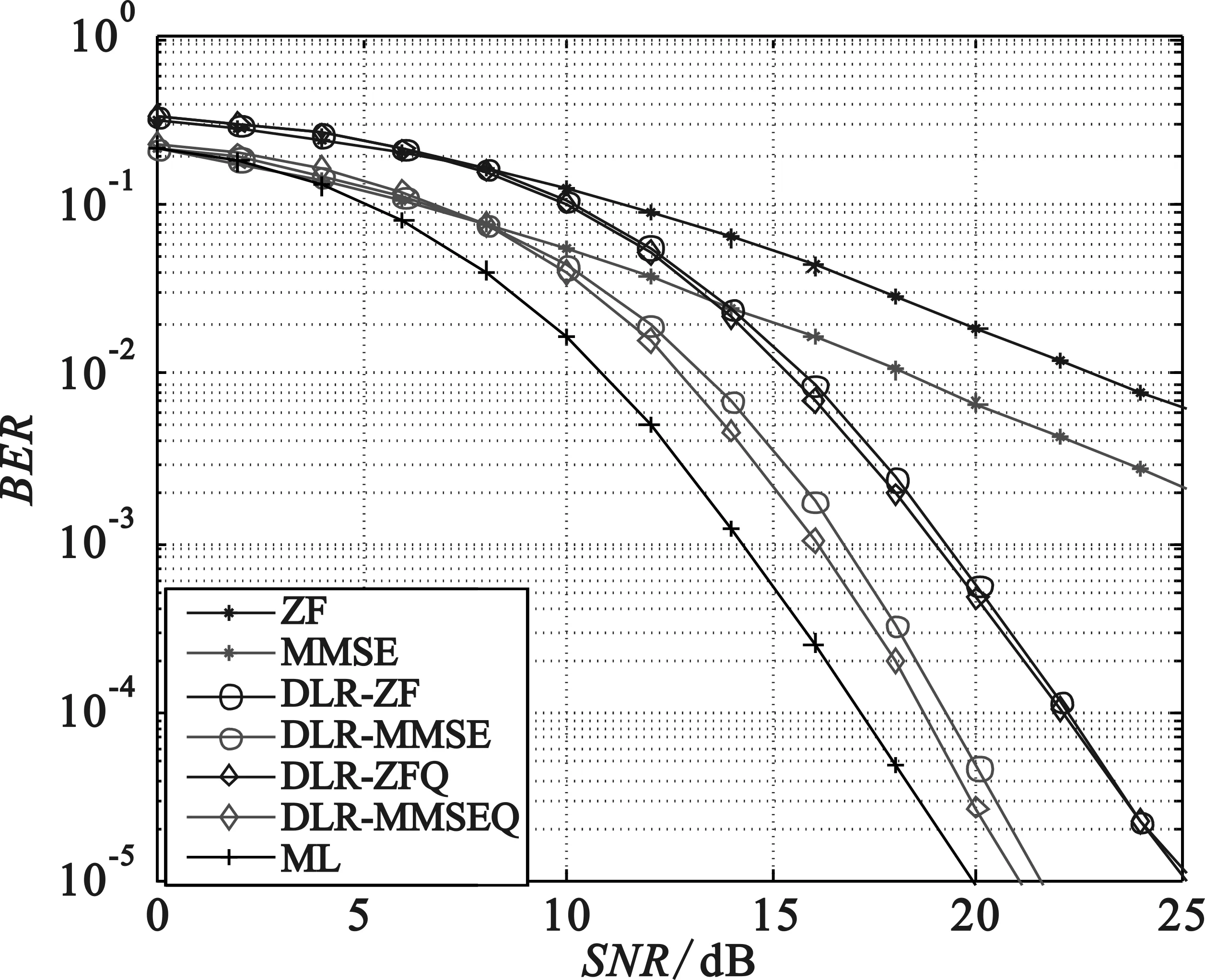
图2 不同检测算法性能仿真

图3 、图4分别给出了不同量化数下基于ZF和MMSE的对偶格基约减算法，图中Q1(本文算法)、Q2、Q3和Q4分别表示选取更新的量化候选点的个数为1、2、3和4情况下的仿真。仿真分析表明，不论是ZF还是MMSE，改进后的量化方法均优于传统的量化方法，从仿真图形中可以看出不同的候选点个数对算法的性能改善几乎无差异，且所选取来更新的候选点的个数越多，算法复杂度越高；而本文算法只选择更新量化误差最大的一个发射符号，其计算复杂度比较低，算法性能也有所改善。

图3 不同量化数下基于ZF检测算法的仿真

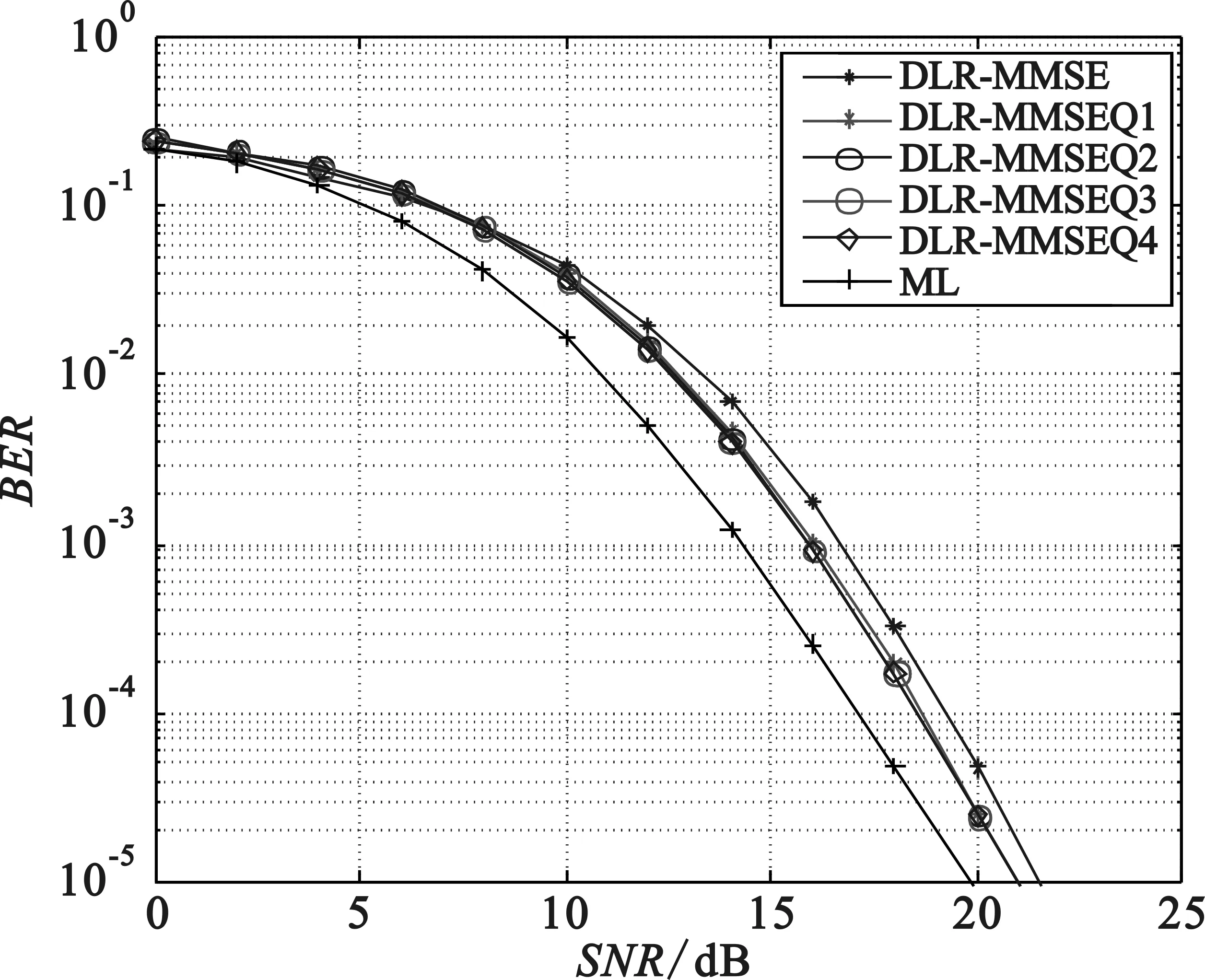
图4 不同量化数下基于MMSE检测算法的仿真

4 结语

本文在传统量化方法的基础上提出了改进量化方法，对仿真结果的分析表明本文方法较传统的方法在误比特率上有所改善，而其计算复杂度也比较低。本文首先对原始信道矩阵求其对偶矩阵，接着对信道对偶矩阵进行格基约减，最后对检测信号进行量化。这里，使用了一种新的量化方法。首先求解出格基约减输出符号中的量化误差，对量化误差进行由大到小的排序，量化误差最大项所对应天线上的发射符号的量化值进行更新，进而获得相应的候选矢量，最终选取最优项作为对偶格基约减算法的最终输出值。仿真结果表明，本文的改进量化方法可以提升检测算法的准确度，以较小的运算量逼近ML检测的性能。

[1] Schnorr C P,Euchner M. Lattice Basis Reduction Improve Practical Algorithms and Solving Subsets Sum Problems, 1993.

[2] MA Xiao-li, WEI Zhang. Performance Analysis for MIMO Systems with Lattice Reduction Aided Linear Equalization[J]. IEEE Transactions on Communications, 2008, 56(2):309-318.

[3] HUAN Yao, Wornall, Gregory W. Lattice Reduction Aided Detectors for MIMO Communication Systems[C]. IEEE Global Telecommunications Conference,2002:424-428.

[4] 郭明喜,沈越泓. 基于对偶格基约减的MIMO检测算法[J].数据采集与处理, 2010, 25(06):696-701. GUO Ming-xi, SHENG Yue-hong. Dual-Lattice-Reduction Algorithm in MIMO Systems[J]. Data Acquisition and Processing, 2010,25(06):696-701.

[5] WANG Xing-lin, GONG Ping, NIU Kai. Dicision Feedback Aided Detection based on Lattice Reduction in MIMO System[C]. IEEE 63rdConference on Vehicular Technology, 2006:1708-1712.

[6] LIU Jin-zhu, XING Song, SHEN Lian-feng. Ordered Successive Noise Projection Cancellation Algorithm for Dual Lattice-Reduction-Aided MIMO Detection[J]. Journal of Southeast University (English Edition), 2013, 29(3):229-234.

[7] Dirk Wubben, Dominik Seethaler, Joakim Jalden,et al. Lattice Reduction[M]. IEEE Signal Processing Magazine, 2011.

[8] Md R U D Rajib, Jin Gyun Chung, Moon Ho Lee. Complex Lattice Reduction Aided Detection for Multiuser MIMO Systems in Dual Basis. IEEE International Symposim on Consumer Electronics, 2014:1-4.

[9] WEI Hou, Tadashi Fujino, Toshiharu Kojima. Efficient Quantization Scheme for Lattice-Reduction Aided MIMO Detection, The 2013 International Conference on Advanced Technologies for Communications, 2013.

[10] 孙艳华, 王浩, 张延华. 复数域格缩减的MIMO检测算法研究[J].电子科技大学学报, 2010, 39(05)：670-675. SUN Ye-hua, WANG Hao, ZHANG Yan-hua. MIMO Detection Algorithm based on Complex Domain Lattice Reduction[J]. Journal of the University of Electronic Science and Technology, 2010, 39(05): 670-675.

A Modified Algorithm of Dual Lattice Basis Aided MIMO Signal Detection

ZHANG Xi1, ZHOU Wei1,2

(1.Chongqing Key Laboratory of Mobile Communications Technology; 2.College of Optoelectronic Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065,China)

Aiming at the problem that traditional quantitative method has large quantization error in dual lattice basis reduction algorithm, a modified quantitative method is proposed. By sorting the value of the quantified error in descending order, a symbol with the largest quantified error is selected as a candidate and the quantization value of this candidate is updated, and thus the new candidate vectors created,and finally the optimal candidate selected as the output solution. Through theoretical analysis and computer simulation, the BER performance of different algorithms under different quantitative methods is studied and the experiment results indicate that the proposed method could achieve better detection performance than the traditional quantify method, and its performance is closer to that of ML detection algorithm.

lattice basis reduction; dual lattice basis reduction; quantization error

10.3969/j.issn.1002-0802.2015.10.004

2015-05-01；

2015-09-10 Received date:2015-05-01；Revised date：2015-09-10

国家高技术研究发展计划(863计划)重点项目(2009AA011302)；重庆邮电大学研究生教育创新计划重点项目(Y201019)；重庆市教委科研项目(K1090513)；重庆市科委重点实验室专项经费。

Foundation Item:National High Technology Research and Development Program of China(2009AA011302);Key Project of Graduate Education Innovation Project,Chongqing University of Post and Telecommunications(Y201019);Scientific Research Project of Chongqing Education Committee(K1090513);Key Lab Special Fund of Chongqing Science & Technology Committee.

TN929.5

1002-0802(2015)10-1116-04