小波分析在沉降监测中的应用

林 楠， 康改霞

(1.河南理工大学测绘与国土信息工程学院，河南 焦作 454000;2.平顶山矿区采煤沉陷区综合治理办公室， 河南 平顶山 467000)



小波分析在沉降监测中的应用

林 楠1， 康改霞2

(1.河南理工大学测绘与国土信息工程学院，河南 焦作 454000;2.平顶山矿区采煤沉陷区综合治理办公室， 河南 平顶山 467000)

由于沉降监测受观测环境、仪器设备及观测人员的影响较大，导致观测数据与真实值之间存在误差。应用小波滤波理论，以MATLAB软件为基础平台采用一维离散小波变换对沉降监测数据进行去噪处理。将数据进行高、低频分解后对细节系数进行分析，并通过小波重构得到的去噪数据对沉降发展趋势进行预测。通过分析发现，小波细节系数能有效地发现沉降波动点，去噪后的数据能有效去除测量粗差。以此论证小波分析在沉降监测中的可行性以及实用性，为施工建设提供有效的指导帮助。

小波去噪； 沉降观测； 一维离散小波变换

小波分析是近20年来发展起来的一种新的时频分析方法，其克服了傅里叶变换在单分辨率上的缺陷，具有多分辨率分析的特点，在时域和频域都有表征信号局部信息的能力。时间窗和频率窗都可以根据信号的具体形态调整，一般情况下，在低频部分(信号较平稳)可以采用较低的时间分辨率，而提高频率的分辨率;在高频情况下(频率变化不大)可以用较低的频率分辨率来换取精确的时间定位。因为这些特点，小波分析可以探测正常信号中的瞬态成分，并展示其频率成分，被称为数学显微镜，广泛应用于各个时频分析领域。由于小波分析在信号去噪、信号奇异性检测、特征提取、数据压缩等方面有着独特的优势，它在变形监测中的应用潜力很大。本文以实际工程为例，探讨小波分析在沉降监测数据中的应用并论证小波分析在工程应用中的有效性及可行性。

1 一维离散小波变换理论[1-2]

1.1 基本理论

处理沉降观测数据适合采用一维离散小波变换，选择MALLAT算法。对信号s进行滤波处理，可以分为以下三步：

(1)分解过程，选择合适的小波基，对原始数据信号进行小波分解；

(2)作用阈值过程，对分解的各层系数选择一个阈值，并对细节系数做阈值处理，即去噪处理；

(3)重建过程，降噪处理后系数通过小波重建恢复原始信号。

对较大尺度的信号进行小波变换，选取其中的低频部分在预案尺度上进行小波变换。即对给定的一个长度为N的信号s，第一步从原始信号s开始，产生两组参数，一组是由低频滤波器Lo_D得到的近似信号cA1，另一组是由高频滤波器Hi_D得到的细节信号cD1，这两组信号都是原信号在滤波器作用下以尺度为2的采样。第二步对低频信号cA1做同样的高频滤波和低频滤波分别得到cD2与cA2，根据研究需要，可以对cA2继续进行滤波分解。

图1 信号小波分解示意图

数学公式表示如下，若尺度为j，分解过程为：

f(x)=Aj-1f(x)=Ajf(x)+Djf(x)，

(1)

其中，信号在空间Vj上的投影为：

(2)

信号在空间Wj上的投影为：

(3)

Ajf(x)是信号f(x)的频率不超过2-j的成分，Djf(x)是频率介于2-j与2-j+1之间的成分。Vj空间尺度系数可以进一步分解下去。分别用cj和dj表示尺度j上的小波系数和尺度系数向量，表示为：

(4)

(5)

原始信号经过滤波器处理之后，就像声音经过滤波处理产生高频部分和低频部分，仅仅获取低频部分同样可以获取声音中的内容信息，但由于去除了高频部分，无法辨别声音的发声源。如果仅获得高频部分而放弃低频部分，接收到的只是一堆噪音，而无法获得有价值的信息。

去噪处理中，所选用的小波阈值既要从细节系数中提取出弱小的有用信号，又要保证在去噪过程中将有用高频信息当作噪声信号去除掉。基于信号降噪准则的光滑性与相似性，本次分析采用启发式阈值选择和极大极小原理选择阈值进行去噪处理。

重建运算是小波分解的逆运算。将分解的近似信号和细节信号去噪后重新组合得到原始信号去噪后的平滑信号。重构的信号为：

(6)

重建过程由尺度最低的近似系数cAj和细节系数cDj开始，分别通过低频和高频重构滤波器，恢复上一尺度的cAj-1。依次重复此过程直到恢复出原始信号为止。

1.2 精度评价

对于去噪效果的评价，使用较广的有以下两种参考指标[3-4]。

(1)信噪比。信噪比是评价信号中去噪效果最广泛使用的量度，信噪比越高说明滤波去噪的效果就越好。信噪比的表达式为

(7)

式中：p1为原信号的功率；p2为去噪信号的功率。

(2)均方根误差。即原始数据与去噪数据之差的标准差的表达式为

(8)

式中：s为原始数据；s1为去噪数据。

2 工程实例

2.1 工程概况

本工程为合肥铁路南站配套城市轨道交通土建工程基坑监测，对合肥南站的1、4、5号线换乘站挖掘2处基坑，共布置监测点94个，自2010年8月21日起先后进行了84次等间隔观测(部分点由于施工原因和监测需求，测量次数少于84次)。此次分析选用Q73号点数据，该点共计84次观测。

2.2 小波分析处理方法及过程[6]

本文采用MATLAB编程语言实现小波算法[5]，选取db4小波进行3层分解。关键代码为：

load Q74.txt; %将Q74号点的数据导入MATLAB程序中

s=Q74; %将Q74的84次观测数据赋值给s

[c,1]=wavedec(s,3,’db4’); %对信号做尺度为3的db4小波分解

[cd1,cd2,cd3]=detcoef(c,l,[1,2,3]); %提取3层细节系数

ca3=appcoef(c,l.’db4’); %提取尺度3的近似系数

subplot(511)；plot(1:84,s);title(‘s’);

subplot(512)；plot(1:l(1),ca3);title(‘ca3’);

subplot(513)；plot(1:l(1),cd3);title(‘cd3’);

subplot(514)；plot(1:l(1),cd2);title(‘cd2’);

subplot(515)；plot(1:l(1),cd1);title(‘cd1’);

%将原信号s以及提取的3个尺度的细节系数和尺度3的近似系数图形显示出来

由以上操作得到图2。

对数据进行降噪处理，采用启发式阈值选择和极大极小原理选择阈值，并选用硬阈值，db4小波进行去噪。关键代码为：

y1=wden(s,‘heursure’,‘h’,‘sln’,3,‘db4’); %启发式阈值去噪

Y2=wden(s,‘minimaxi’,‘h’,‘sln’,3,‘db4’); %极大极小原理阈值去噪

thr1=thselect(s,‘heursure’); %启发式阈值

thr2=thselect(s,‘minimaxi’); %极大极小原理阈值

重建小波代码为：

A3=wrcoef(‘a’,c,l,‘db4’,3); %重建3层近似系数

D1=wrcoef(‘d’,c,l,‘db4’,1);

D2=wrcoef(‘d’,c,l,‘db4’,2);

D3=wrcoef(‘'d’,c,l,‘db4’,3); %重建1、2、3层细节系数

综上得到去噪信号与原始信号对比图(见图3)。

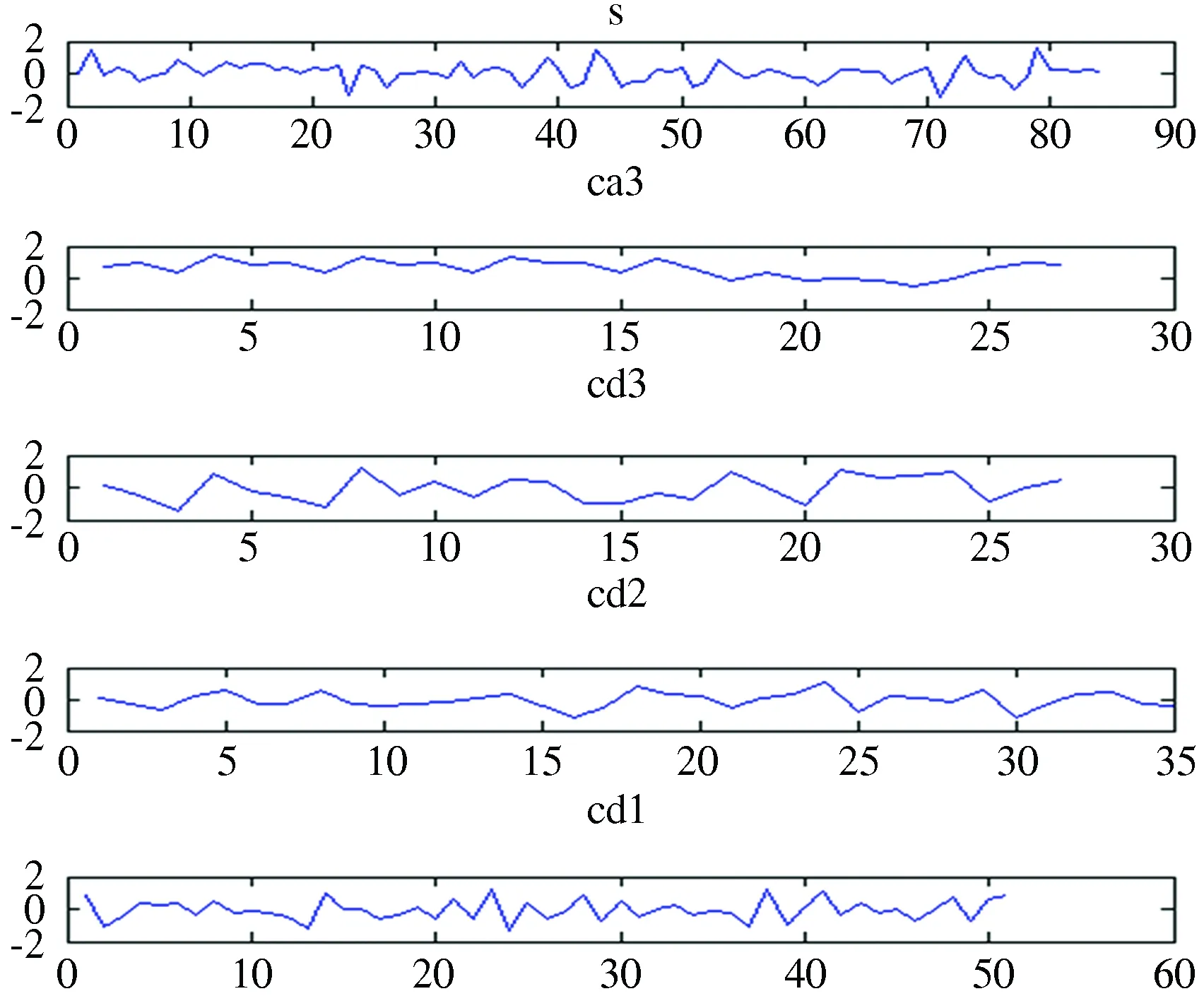
图2 原始数据s在db4小波下的尺度为3的分解示意图

图3 去噪重构数据与原始数据对比图

2.3 数据分析与精度评价

由图3可知两种阈值去噪所得的数据都能大体表现出原始观测数据的发展趋势。原始信号s存在少量的高频系数位于噪声范围之中时，选用的两种阈值方法在去噪方面更加的保守方便[7]，能够极大的提取出弱小的信号，不容易丢失真实的信号部分。联系图2可知，cd2与cd3的细节系数均相对平稳，但cd1高频系数较多，极大极小原理阈值去噪效果保持的较为稳定，而启发式阈值选择保证了原数据大体趋势，但细节显示不明显，可能是在去噪过程中将有用的信号高频部分当作噪声部分去除。根据两种去噪的对比示意图发现，启发式阈值去噪的信号比较平滑，但丢失了部分的细节成分。而极大极小原理阈值去噪却很好地避免了这点缺陷。

对于极大极小原理选择阈值去噪的数据其信噪比为131.762分贝，均方根误差为0.120 5 mm，都在限定范围之内,预测效果较好。由两种降噪信号不难发现，从观测开始一直到第60次观测，基坑发生着持续沉降，波动较大的部分在9到20次观测以及42到51次观测之间，60次观测后沉降趋于稳定，但到了68次观测时沉降又出现较大的波动。根据沉降监测数据以及图表分析反馈的信息分析沉降出现较大波动的原因，由现场工程资料分析得，第71次观测时在此基坑73号观测点旁另一处基坑开始动工,可能使地层发生挤压变形致使73号点继续发生沉降。参照第68次观测后的原始数据以及小波去噪数据可知，沉降仍不平稳，且数据波动依旧很大，因此需要继续对基坑进行沉降监测，直至沉降平稳为止。

2.4 结论

(1)小波分析方法能有效地去除观测粗差，使去噪声后的数据更接近真实数值。但需要选取合适的阈值，防止去噪过程中将高频信号当作噪声一并去除。

(2)对于沉降数据出现较大波动时，可以从细节系数(即高频部分)及时的得到反馈，分析沉降出现较大波动的原因，为工程的顺利进行提供参考依据。

3 结束语

本文应用小波分析对基坑沉降数据进行了滤波去噪处理，并对处理结果进行了更深一步的分析。通过合肥南站基坑监测工程实例发现，小波滤波去噪可以减小原始数据的误差，滤波后得到的数据较原始数据更加平滑且真实可靠。对监测数据突然出现较大变动时，小波滤波可以及时的反映出来。由本次工程可见小波分析具有较大实践价值，对于沉降监测具有很好的预测效果。

[1] 潘泉，张磊，张洪才，等. 小波滤波方法及应用[M]. 北京：清华大学出版社，2005.

[2] 樊启斌. 小波分析[M]. 武汉：武汉大学出版社，2008.

[3] 高成. Matlab小波分析与应用[M]. 北京：国防工业出版社，2007.

[4] 葛哲学，沙威. 小波分析理论与MATLABR2007实现[M]. 北京：电子工业出版社，2007.

[5] 王建敏,周鹏,王旭. 小波阈值去噪法在高铁沉降观测数据处理中的应用研究[J]. 矿山测量, 2011, 3(3): 69-71.

[6] 王建波,栾元重,许君一，等. 小波分析桥梁变形监测数据处理[J]. 测绘科学, 2012, 37(3): 79-81.

[7] 郭健. 基于小波分析的桥梁健康监测方法[J]. 工程力学,2006,12(23)：129-135.

[8] 夏秋. 小波分析在GPS变形监测数据处理中的应用[J]. 地理空间信息, 2011,12(9)：41-44.

[9] 方圣辉,乐源,梁琦. 基于连续小波分析的混合植被叶绿素反演[J]. 武汉大学学报:信息科学版,2015(3):296-302.

Application of wavelet analysis in settlement data

LIN Nan1， KANG Gai-xia2

(1.SchoolofSurveyingandLandInformationEngineering,HenanPolytechnicUniversity,Jiaozuo454000,China;2.ComprehensiveManagementOfficeofPingdingshanCoalMiningSubsidence,Pingdingshan467000,China)

Due to the observed deformation monitoring environmental impact, equipment and observers by leading real data and the actual observation data error exists. In this paper, denoising is made by means of wavelet filtering theory and MATLAB software-based platform with a one-dimensional discrete wavelet transform of data. After deviding the data into high and low frequency, detail coefficients are analyzed and wavelet reconstruction is made in detail. Finally we get noise-elimination data and predict the developing trend of sedimentation. The analysis revealed that the wavelet detail coefficients can effectively detect fluctuations settlement points, data denoised measures can effectively remove gross error. With this, the feasibility of wavelet analysis in subsidence monitoring and practicality is discussed, which provides effective guidance for construction.

wavelet denoising; settlement observation; one-dimensional discrete wavelet transform

2014-12-17

林 楠(1991-),男,安徽马鞍山人,硕士研究生。

1674-7046(2015)02-0073-04

10.14140/j.cnki.hncjxb.2015.02.016

TU411.7;TU431

A