细丝弓技术舌侧内收上颌前牙的三维有限元生物力学分析

张向凤 王超 夏熹 邓锋 张翼

重庆医科大学附属口腔医院正畸科，口腔疾病与生物医学重庆市重点实验室，重庆 401147

随着人们对于正畸矫治过程美观要求的提高，舌侧矫治日益成为成人矫治的重要选择。在舌侧矫治过程中，由于舌侧面的牙弓长度显著小于唇侧长度，因此相同大小的外力作用于舌侧矫治系统所产生的牙齿应力应变显著大于唇侧矫治系统[1-3]。

在唇侧固定矫治技术中，以Tip-Edge为代表的细丝弓矫治技术通过早期不粘接前磨牙托槽等方式增加托槽间距，从而降低牙周膜的应力应变；同时，单翼托槽的设计使得牙齿移动过程中成角阻力减小，有效提高了牙齿移动的效率[4]。可以设想，将唇侧细丝弓技术的力学系统应用于舌侧矫治系统是否可以得到与传统舌侧矫治不同的生物力学效应，以减小牙齿的应力以及提高牙齿移动效率呢？本研究建立细丝弓技术舌侧内收上颌前牙的三维有限元模型，探讨该模型下的生物力学效应。

1 材料和方法

1.1 细丝弓技术舌侧内收上颌前牙的三维有限元模型的建立

将上述3D模型导入到CAD软件Solidworks中建立舌侧托槽和弓丝模型（图1）；托槽的规格参照STB托槽（Ormco公司，美国），弓丝为0.406 4 mm的不锈钢圆丝，使得弓丝的形状与上颌牙列舌侧外形相匹配。调整模型，定义坐标系：原点定义为咬合平面上中间对称轴与两个第一磨牙连线的交点，左右方向为X轴方向，前后方向为Y轴方向，垂直方向为Z轴方向。

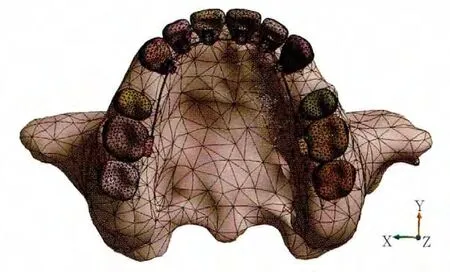
图1 舌侧上颌前牙内收三维有限元模型面观Fig 1 Occlusal view of three-dimensional f inite element analysis model of anterior teeth retraction system in lingual orthodontics

1.2 边界约束条件的定义

将模型导入到有限元软件ANSYS Workbench，用Solid189四面体单元进行网格划分。牙齿—托槽、牙齿—牙周膜、牙槽骨—牙周膜、皮质骨—松质骨之间用bonded连接；托槽—弓丝采用No separation连接，允许其发生小量切向位移，限制其法向位移；颊面管—弓丝采用Cylindral Joint连接，允许颊面管有轴向平移及旋转，限制并约束其他4个自由度。

1.3 材料属性与载荷设置

模型中的各种材料属性均定义为均质性、各向同性的线弹性材料。材料变形为小变形。材料的弹性模量与泊松比如表1所示[5-6]。工况设计：Ⅱ类牵引力作用于上颌尖牙托槽近中弓丝上，牵引力方向斜向后下、大小0.556 N。不锈钢圆丝后倾曲作用于上颌第一磨牙颊面管近中2 mm，分别计算当后倾曲扭矩为15、30、45、60、75 Nmm时上颌中切牙、侧切牙、尖牙的初始位移以及牙周膜静水压分布。

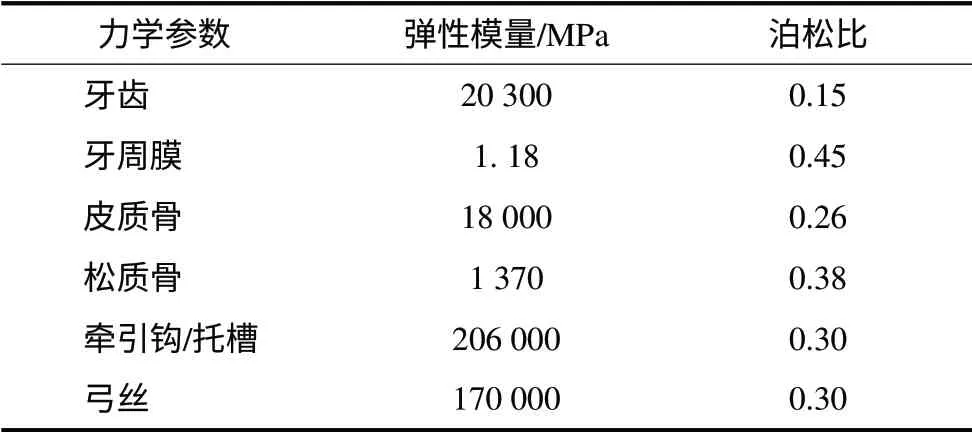
表1 三维有限元模型的材料参数Tab 1 Material properties required in the three-dimensional f inite element model

2 结果

2.1 舌侧细丝弓力系下上颌前牙牙周膜静水压分布

在舌侧细丝弓力系作用下，上颌中切牙、侧切牙以及尖牙的颊侧根尖和舌侧颈缘出现压应力集中区，而舌侧根尖和颊侧颈缘则出现张应力集中区（图2）。在15 Nmm后倾曲力矩和0.556 N Ⅱ类牵引力的协同作用下，上述4个应力集中区的静水压均显著小于毛细血管压。

当磨牙后倾曲力矩从15 Nmm增加至75 Nmm时，上颌中切牙颈缘牙周膜静水压逐渐从-3.748 kPa增加至-5.692 kPa，根尖牙周膜静水压逐渐从-3.724 kPa增加至-6.400 kPa，仍显著小于毛细血管压（16 kPa）[7-8]。上颌侧切牙牙周膜静水压应力分布及变化趋势与中切牙一致。对上颌尖牙而言，在15 Nmm力矩作用下，根尖牙周膜静水压应力为-10.982 kPa；当后倾曲力矩为30 Nmm时，根尖牙周膜的静水压应力为-21.209 kPa，大于毛细血管压；当力矩增加至75 Nmm时，根尖牙周膜的静水压应力最高可达-54.832 kPa（表2）。

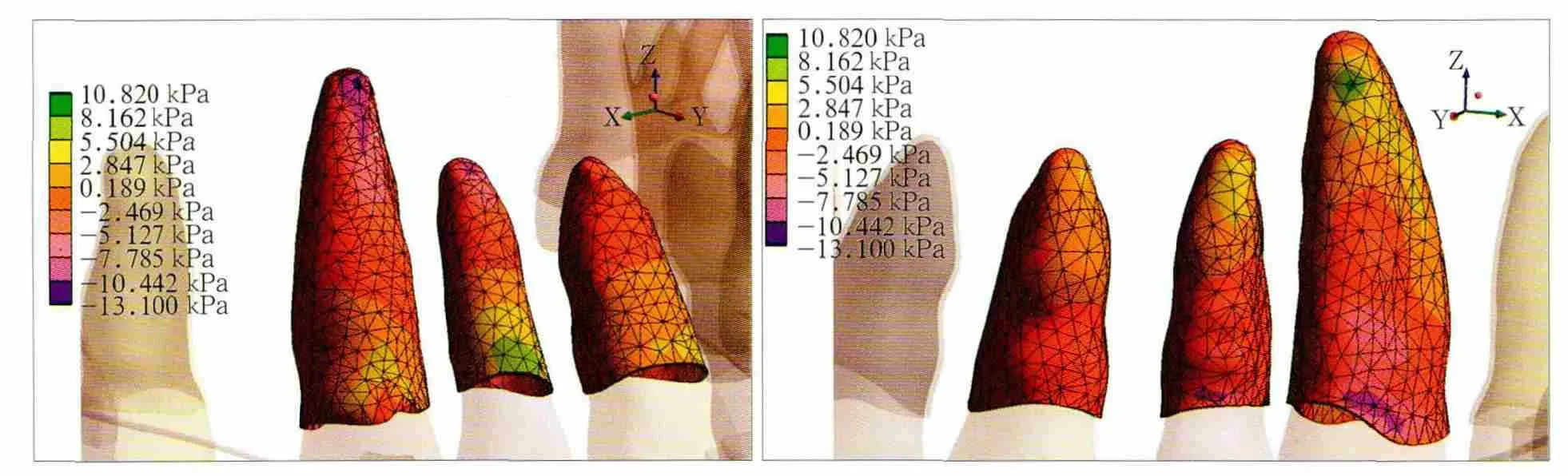
图2 15 Nmm力矩时上前牙牙周膜静水压唇侧（左）及舌侧（右）观Fig 2 The labial(left)and lingual(right)view of periodontal ligament strain distribution of maxillary anterior teeth under 15 Nmm moment

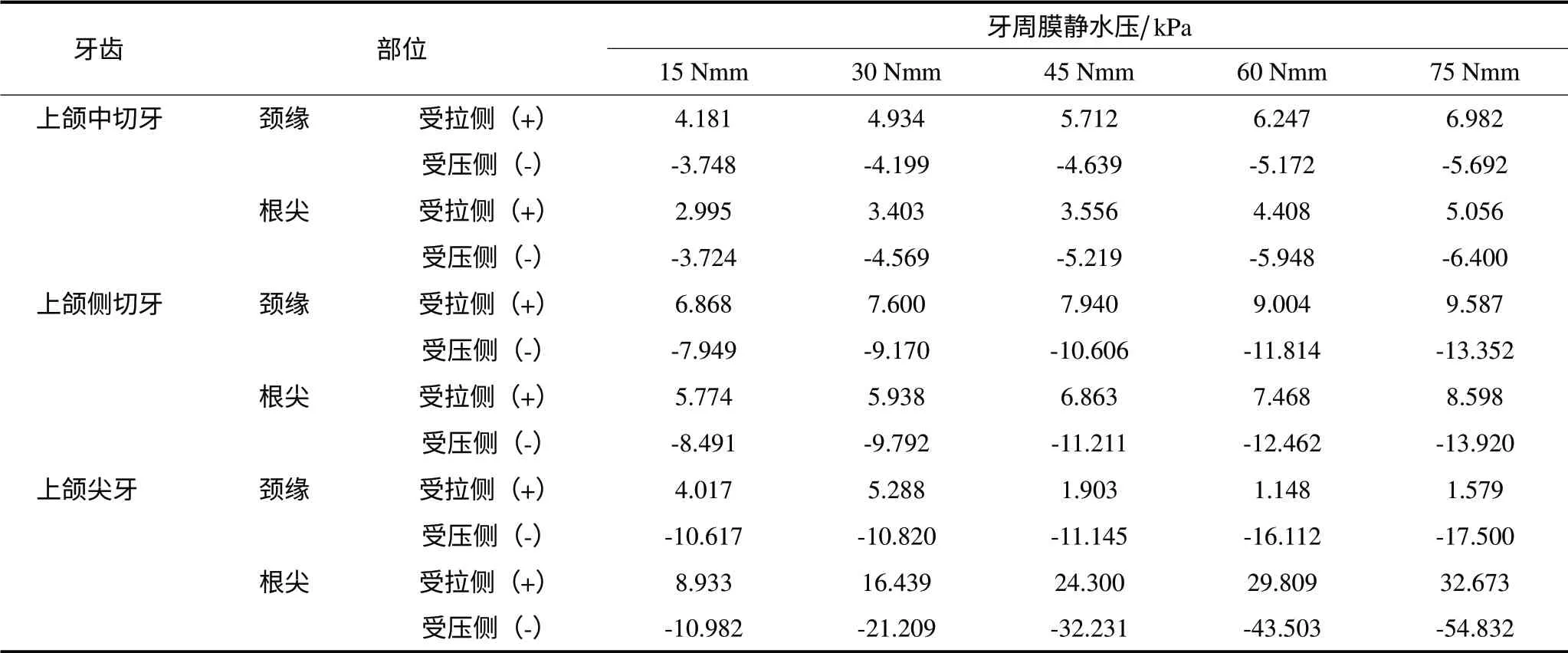
表2 不同的后倾曲扭矩对上颌前牙牙周膜静水压分布的影响Tab 2 Effect of maxillary anterior teeth periodontal ligament hydrostatic pressure distribution under different tip back bend moment

2.2 舌侧细丝弓力系作用下上颌前牙初始位移

在0.556 NⅡ类牵引和15 Nmm力矩后倾曲的协同作用下，上颌中切牙Y轴方向上切缘出现远中方向初始位移，而根尖则出现唇向位移，即上颌中切牙产生远中倾斜移动；Z轴方向上上颌中切牙切缘产生伸长初始位移，根尖产生压入初始位移。随着后倾曲所产生力矩的增加，在Y轴方向上，切缘远中方向初始位移逐渐减小，根尖唇向初始位移逐渐增加；Z轴方向上，上颌中切牙切缘以及根尖的压入初始位移都随着磨牙后倾曲力矩的增加而逐渐增加（图3左）。上颌侧切牙与尖牙的初始位移移动趋势基本与上颌中切牙一致。与上颌中切牙不同的是，即便在后倾曲力矩为15 Nmm作用下，上颌尖牙的切缘和根尖也均出现压入移动（图3中、右）。

图3 不同后倾曲力矩作用下上颌中切牙（左）、侧切牙（中）及尖牙（右）的初始位移Fig 3 The initial displacement of upper central incisor(left),lateral incisor(middle)and canine(right)under different moment produced by tip back bend

3 讨论

自20世纪70年代美国的Kurz医生和日本的Fujita医生分别发明舌侧矫治系统以来，舌侧矫治因其美观方面的巨大优势受到越来越多的患者的青睐[9]。舌侧矫治器发展的初衷是由于患者对于治疗过程中的美观及隐私要求，以及避免牙齿表面由于正畸所导致的脱矿问题。在后续应用过程中，临床正畸医生逐渐发现舌侧矫治技术和唇侧矫治技术具有完全不同的生物力学效应。有学者[9-10]建立舌侧矫治技术数学模型以进行理论受力分析，分别对不同唇倾度的上颌前牙托槽施加垂直向的压入力，分析该力对唇、舌侧矫治力系上颌前牙移动趋势的影响，结果发现：较唇侧矫治系统而言，舌侧矫治系统上颌前牙在受力时更容易产生舌向倾斜移动；同时还发现，在舌侧矫治力系统中的载荷挠曲率更高，获得理想的轻力更为困难。Liang等[3]建立上颌骨及上颌切牙的三维有限元模型，分析颊舌侧施加力和力矩时牙齿的初始位移以及牙周膜应力应变分布的区别，同样发现舌侧矫治力系较唇侧矫治力系更容易使上前牙发生舌向倾斜移动。此外，由于舌侧空间较为狭小，较小的托槽间距使得弓丝难以入槽以及入槽后牙齿受力过大，从而影响牙周组织健康以及限制了牙齿的快速移动。在唇侧的Tip-Edge矫治力系中，通过使用高弹性低尺寸的不锈钢圆丝可以有效减低载荷挠曲率以及托槽和弓丝间的摩擦力，而且由于前磨牙常规不粘接托槽，所以进一步降低了载荷挠曲率从而达到牙齿快速移动的生物力学效果。为了探索在舌侧矫治力系中是否可以采用类似于唇侧的细丝轻力矫治技术，以减小载荷挠曲率，同时获得快速有效的牙齿移动，本研究建立了细丝弓技术舌侧内收上颌前牙的三维有限元模型对这一问题进行生物力学层面的初步探讨。

在唇侧矫治系统中，主流矫治力系分为直丝弓矫治力系和细丝弓矫治力系。直丝弓矫治力系强调牙齿的整体移动，通常设计的托槽间距较小，临床力值较大；而细丝弓矫治力系强调牙齿的倾斜移动，通过序列粘接托槽以及选择单翼托槽的方式增加托槽间距而降低正畸矫治力，通过0.556 N的颌间牵引力就足以使牙齿产生快速移动。目前关于舌侧的细丝矫治系统研究尚少，尽管从理论上推理在舌侧运用细丝矫治力系是可行的，但在进入临床应用之前仍有必要进行系统的生物力学分析。

三维有限元法自20世纪70年代被运用于口腔领域，目前对正畸牙移动的三维有限元生物力学研究已经不再局限于单个牙的移动，越来越多的学者开始尝试建立复杂的正畸矫治力系三维有限元模型从系统的观点对整个矫治力系进行全方位的研究。三维有限元法是研究正畸牙移动的重要方法，将分析的连续实体离散成有限个单元，以各单元的结合体代替原连续体，并逐个研究每个单元的力学性质，建立单元的刚度方程，然后根据给定的载荷条件将其组集成总体刚度的方程，按照给定的边界位移条件求解总体方程组，得到单元所有节点的位移，并据此计算单元的内力和应力。由此可见，有限元法对各种几何形态、材料性质以及复杂的支持条件和加载方式都能进行分析，并且保证了模型的可重复性[11-12]。运用三维有限元方法，可以系统研究正畸力作用下每个牙齿的初始位移，牙根、牙槽骨的应力和应变，从而分析牙齿移动趋势以及牙根和牙槽骨发生吸收的可能性[13-15]。

理想的正畸矫治力系应该可以有效且快速地移动牙齿，牙齿的移动方式可控而不伴有严重的组织损伤，这就是最适力的概念[16]。Melsen[17]发现，相同的外力作用于不同的矫治力系统，产生的牙周膜应力—应变是不同的，因此临床正畸医生找出外力与牙周膜应力—应变反应间的关系至关重要。三维有限元法作为一种经典的数值仿真分析法为这一问题的解决提供了稳定可靠的研究方法。

静水应力是一个分析正畸牙移动的重要指标。静水应力的正负表示牙周膜受拉还是受压的应力状态。牙周膜内静水应力的多少通常用于衡量对牙根吸收的影响。Rygh[8]认为，当牙周膜静水压大于牙周膜毛细血管压（16 kPa）时，牙周膜内的毛细血管会发生崩塌导致局部牙周组织坏死，这时巨噬细胞及其产生的破骨因子聚集使牙根发生吸收。本研究结果表明，在舌侧细丝弓力系作用下，上颌中切牙和侧切牙的牙周膜静水压始终小于毛细血管压，根据Rygh的牙根吸收原理推测，该力系作用下牙齿不易发生牙根吸收。随着后倾曲力矩的增加，上颌尖牙的牙周膜静水压可能超过毛细血管压，这可能与尖牙更靠近后倾曲因此承受更多的后倾曲所产生的应力—应变有关。

牙齿的初始位移是衡量力系统作用下牙齿移动趋势的重要指标，代表加力瞬间各个牙齿移动的方向及移动量[18]。本研究结果显示，上颌尖牙的初始位移明显大于上颌中切牙和侧切牙，这可能与上颌尖牙距离Ⅱ类牵引力的作用点以及后倾曲较近有关。

内收过程中上颌前牙的垂直向控制是临床矫治设计考虑的重点。在垂直方向上，上颌尖牙可获得Z轴方向压入的初始位移，而上颌中切牙和侧切牙则出现Z轴方向伸长的初始位移；随着后倾曲力矩的增加，中切牙、侧切牙以及尖牙垂直方向压入的初始位移逐渐增加。由于本文是研究受力瞬间牙齿的初始位移，加力瞬间初始位移并不能反应牙齿在一个加力周期的总移动量，因此有必要在后续研究中运用骨重建理论建立更为复杂的动态三维有限元模型进行分析。

在Y轴方向上，上颌尖牙远中初始位移显著大于中切牙和侧切牙。在Ⅱ类牵引力不变的情况下，随着后倾曲力矩的增加上颌尖牙的远中初始位移逐渐增加；由此可以推断，后倾曲通过弓丝—托槽力系统对尖牙产生了向后上方向的力，而非单纯的压低力。

综上所述，本研究通过建立细丝弓技术舌侧内收上颌前牙的三维有限元模型，系统性研究了后倾曲对舌侧细丝弓系统的生物力学效应的影响。尽管正畸牙移动是一个周期性的动态骨重建过程，本研究仍通过分析加力瞬间牙齿初始位移和牙周膜应力分布对该力系作用下牙齿的移动趋势和移动的安全性进行了全面地评估，从而为该技术的临床应用提供了可靠的生物力学依据。

[1]Long H,Zhou Y,Pyakurel U,et al.Comparison of adverse effects between lingual and labial orthodontic treatment[J].Angle Orthod,2013,83(6):1066-1073.

[2]Lombardo L,Stefanoni F,Mollica F,et al.Three-dimensional f inite-element analysis of a central lower incisor under labial and lingual loads[J].Prog Orthod,2012,13(2):154-163.

[3]Liang W,Rong Q,Lin J,et al.Torque control of the maxillary incisors in lingual and labial orthodontics:a 3-dimensional f inite element analysis[J].Am J Orthod Dentofacial Orthop,2009,135(3):316-322.

[4]Parkhouse RC,Parkhouse PS.The Tip-Edg torquing mechanism:a mathematical validation[J].Am J Orthod Dentofacial Orthop,2001,119(6):632-639.

[5]杨宝宽,王林,严斌,等.利用MIMICS和CATIA软件辅助建立包含方丝弓矫治器的上颌三维有限元模型[J].实用口腔医学杂志,2010,26(3):329-332.

[6]Pelsue BM,Zinelis S,Bradley TG,et al.Structure,composition,and mechanical properties of Australian orthodontic wires[J].Angle Orthod,2009,79(1):97-101.

[7]Field C,Ichim I,Swain MV,et al.Mechanical responses to orthodontic loading:a 3-dimensional f inite element multitooth model[J].Am J Orthod Dentofacial Orthop,2009,135(2):174-181.

[8]Rygh P.Ultrastructural changes in pressure zones of human periodontium incident to orthodontic tooth movement[J].Acta Odontol Scand,1973,31(2):109-122.

[9]Romano R,Geron S,Echarri P.Lingual &esthetic orthodontics[M].London:Quintessence Publishing,2011:677-679.

[10]Geron S,Romano R,Brosh T.Vertical forces in labial and lingual orthodontics applied on maxillary incisors—a theoretical approach[J].Angle Orthod,2004,74(2):195-201.

[11]Cattaneo PM,Dalstra M,Melsen B.The f inite element method:a tool to study orthodontic tooth movement[J].J Dent Res,2005,84(5):428-433.

[12]Murakami N,Wakabayashi N.Finite element contact analysis as a critical technique in dental biomechanics:a review[J].J Prosthodont Res,2014,58(2):92-101.

[13]陈新民,赵云凤.口腔生物力学[M].北京:科学出版社,2010:18-19.

[14]王晓玲,徐宝华,梁伟,等.舌侧正畸上颌第一磨牙牙根及牙周组织的应力分析[J].口腔医学,2008,28(7):355-357.

[15]张翼,夏熹,邓锋,等.Tip-Edge力系后倾曲对上颌磨牙初始位移影响的三维有限元分析[J].华西口腔医学杂志,2012,30(3):329-332.

[16]Ren Y,Maltha JC,Kuijpers-Jagtman AM.Optimum force magnitude for orthodontic tooth movement:a systematic literature review[J].Angle Orthod,2003,73(1):86-92.

[17]Melsen B.Tissue reaction to orthodontic tooth movement—a new paradigm[J].Eur J Orthod,2001,23(6):671-681.

[18]Kojima Y,Fukui H.A numerical simulation of tooth movement by wire bending[J].Am J Orthod Dentofacial Orthop,2006,130(4):452-459.