基于测月雷达机制月壤相对介电常数反演方法模拟研究*

邢树果，苏 彦

(1. 中国科学院国家天文台，北京 100012；2. 中国科学院大学，北京 100049)

CN 53-1189/P ISSN 1672-7673

基于测月雷达机制月壤相对介电常数反演方法模拟研究*

邢树果1,2，苏 彦1

(1. 中国科学院国家天文台，北京 100012；2. 中国科学院大学，北京 100049)

嫦娥三号卫星于2013年12月2日发射，并成功着陆月球，其巡视器上搭载的测月雷达实现了首次雷达就位探测月球。基于测月雷达的探测机制，给出了两种计算月壤相对介电常数的方法，标定件标定法和双天线时延法，并通过仿真验证了两种计算方法的有效性，文中同时给出了两种计算方法存在的局限性，为后期基于嫦娥三号雷达数据进行月球次表层的介电特性反演提供了重要依据。

射电天文学；测月雷达；相对介电常数；月球

嫦娥三号卫星在2013年12月2日于西昌卫星发射中心成功发射，并与12月14日21时成功着陆月球雨海北部，随后着陆器与“玉兔号”月球车巡视器成功分离。测月雷达作为“玉兔号”月球车的重要载荷之一，在月面开展工作，获取了大量的科学数据。

嫦娥三号巡视器搭载的测月雷达是一种工作于无载频毫微秒脉冲的时间域探测雷达，采用收发天线分置。测月雷达发射机产生超宽带的无载频毫微秒脉冲，经过发射天线向月面下辐射电磁波信号，信号在月壤和月岩介质的传播过程中，如果遇到不均匀层、不同介质交界面时，将产生电磁波反射。测月雷达接收天线接收到该反射信号后，经过接收机放大、采样后获得相应的回波探测数据，通过对回波数据分析、处理，进而得到巡视器行走区域内月壤厚度分布以及月壳次表层岩石地质结构信息。嫦娥三号巡视器搭载的测月雷达为双通道天线雷达，一通道工作中心频率为60 MHz，厚度分辨率为米级，探测深度大于100 m；二通道工作中心频率为500 MHz，厚度分辨率小于30 cm，探测深度大于30 m。测月雷达的科学目标是探测在月球车行进线路上的月壤厚度及次表层结构。

月壤及月球次表层结构的研究，不仅是了解月球地质历史的关键，更有助于月球局地或全球热史研究及地球-月球起源关系的研究[1]。一些学者通过在不同波段以及利用不同探测模式对月球进行观测，进而得到月壤的厚度分布情况[2-6]，同时，月壤相对介电常数是研究月壤介电特性、月壤厚度的关键参数[7]。介质的相对介电常数是指假定真空介电常数为1，介质的介电常数与真空的介电常数的比值。同时对阿波罗(Apollo)回归样品的分析，得到了月壤相对介电常数与月壤密度的经验公式[8]，预估雨海地区月壤的相对介电常数为2.3～3.5。本文中基于测月雷达的工作原理，给出了两种计算月壤相对介电常数的方法，并通过模拟仿真验证了计算方法的有效性。

1 相对介电常数计算方法

基于测月雷达的工作原理及电磁波在介质中的传播特性，给出了两种计算月壤相对介电常数的方法，标定件标定法和双天线时延法。

1.1 标定件标定法

测月雷达在月面工作时，电磁波由空气进入月壤，由于空气与月壤存在阻抗差异，会产生电磁波的反射与透射，其中反射的电磁波会被接收天线接收。通过对比接收的信号强度与输入的信号强度，可以推算出电磁波在该月壤与空气分界面处的反射系数。同时，由于反射系数是两种介质相对介电常数的函数，已知真空的相对介电常数为1，进而可以计算出月壤的相对介电常数。

在实际计算时，由于天线距离地面存在一定高度并且电磁信号在传播路径上存在衰减，所以无法精确知道电磁波入射介质表面时的强度及反射的强度。可以采用图1的方法，得到标定介质的反射强度及月壤的反射强度。

图1 标定件标定法原理示意图

Fig.1 Illustration of the calibration method for the measurement of the relative permittivity of the lunar regolith

式中，Er_c为天线接收的标定介质反射强度；Er_m为天线接收的月壤反射强度；Eo为天线发射强度；r_c为标定介质分界面的反射系数；r_m为月壤分界面的反射系数；D为电磁波在路径上的衰减；δ为球面波在该传播路径上的增益系数。

电磁波在介质分界面的反射系数与介质的波阻抗差异有关，真空中的本征阻抗约为377 Ω，当不考虑介质损耗特性，介质的波阻抗可以表示为[9]

整理后得到下面的计算公式：

(1)

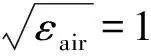
1.2 双天线时延法

嫦娥三号巡视器搭载的测月雷达二通道天线为蝶形(Bowtie)天线，安装在月球车底部，该天线为单发双收。如图2，A接收天线距离发射天线La=15.4 cm，B接收天线距离发射天线距离Lb=31.7 cm，天线距离地面高度d=30 cm。

双天线时延法的工作原理如图3，天线距离地面的高度为d，A、B接收天线距离发射天线的距离分别为La和Lb，均匀月壤的厚度为D，相对介电常数为εm，电磁波由发射天线到A接收天线的时延为ta，到达B接收天线的时延为tb。

利用电磁波在介质中的传播特性，可以得到如下方程组：

(2)

在上述方程组中，ta、tb、d、La、Lb已知，c取电磁波在真空中的传播速度，利用上面的方程可以求出月壤的相对介电常数εm及月壤厚度D。在利用该方法求解月壤介电常数时，首先要从雷达回波数据中找出月壤与下层介质分界面处的时延值，利用该时延值，可以同时求出月壤厚度及月壤的相对介电常数。

图2 测月雷达二通道天线结构示意图

Fig.2 Illustration of the structure of the Channel-2 antenna of the LPR

图3 双天线时延法原理示意图

Fig.3 Illustration of the signal-delay measurement with a dual-antenna receiver

2 仿真验证

通过建立模拟仿真模型，验证两种计算月壤相对介电常数的有效性。具体的仿真流程如下：首先搭建电磁波传播的介质模型，介质模型中假定介质的介电常数，当电磁波输入信号在模型中运行之后，模型的输出即雷达接收信号，通过对雷达接收信号利用标定件标定法和双天线时延法计算，反演出介质的介电常数，然后对比反演出的介电常数与起初假定的介电常数，并进行分析。

测月雷达二通道发射机发射波形选用雷克子波，发射机输出波形如图4，其函数表达式为

2.1 标定件标定法模型仿真

构建仿真模型如图5，模型大小为1m×1m，空气0.6m，月壤为0.4m，发射天线距离接收天线0.3m，天线距离介质表面的高度为0.3m，标定介质选择相对介电常数为10，初设月壤的相对介电常数为2.9。

发射波形选择雷克子波，中心频率为500MHz，如图6，得到了3条仿真结果曲线，第1条实线型曲线，代表由发射天线发射的电磁波信号被接收天线接收的波形，简称直达波；第2条划线型曲线，代表模型中介质为标定介质的回波结果，该曲线包含了电磁波信号在标定介质分界面的反射信号及直达波信号；第3条点线型曲线，代表模型中介质为月壤的回波结果，该曲线包含了电磁波信号在月壤分界面的反射信号及直达波信号。

图4 发射机发射波形

Fig.4Atypicalsignalproducedbythetransmitter

图5 标定件标定法仿真模型

Fig.5 The configuration in the simulation of the calibration method

图6 标定件标定法的仿真结果

Fig.6 The result of the simulation of the calibration method

为了更加准确地反演月壤的相对介电常数，在计算时，应该去除直达波对回波信号的影响，所以将上述仿真得到的标定介质的回波信号和月壤的回波信号分别减去直达信号，结果如图7。取第1个波峰位置，标定介质的反射信号强度为0.220 1，月壤的反射信号强度为0.111 7。

结合第2部分给出的计算公式，Er_m=0.111 7，Er_c=0.220 1，εc=10，εair=1，代入公式得εm=2.9，与先前预设的月壤相对介电常数一致。

2.2 双天线时延法模型仿真

构造的模型如图8，模型大小为1 m×6 m，模型从上到下分别是空气、月壤和月岩。空气厚度为0.6 m，月壤厚度为3 m，月岩厚度为2.4 m，3个天线距离月壤的高度为0.3 m，其中A接收天线距离发射天线0.154 m，B接收天线距离发射天线0.317 m。初始设定月壤相对介电常数取2.9，月岩的相对介电常数为9。

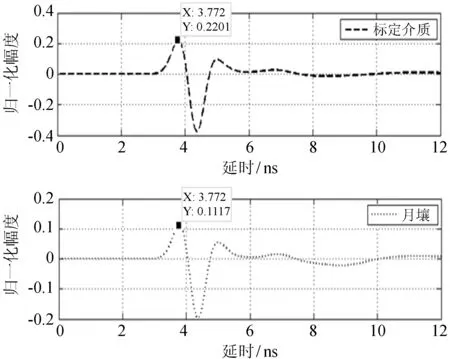
图7 减去直达波后的结果图

Fig.7 The result of the simulation of the calibration method corrected for the direct wave

图8 双天线时延法仿真模型

Fig.8 The configuration in the simulation of the signal-delay measurement with the dual-antenna receiver

在模拟仿真时，A接收天线接收的信号主要包含了3部分，直达波、空气与月壤的反射波、月壤与月岩的反射波。同样，B接收天线接收的信号主要包括了3部分，直达波、空气与月壤的反射波、月壤与月岩的反射波。仿真结果如图9。

由于信号子波存在一定的时间宽度，所以无法精准确定信号的起点，因此采用信号在月壤与月岩分界面的时延差作为输入的时延值，进而计算公式可修改为

(3)

实际数据处理时，可以扣除地面反射波的影响，如图10中，在单道的雷达波形图上，第1个波形为直达波，第2个波形为月壤与月岩分界面的发射波。在该图上已经扣除了地面发射回波的影响。其中，ta=37.759 43 ns，tb=37.771 23 ns，tair_a=2.087 264 ns，tair_b=2.617 925 ns，d=30 cm，La=15.4 cm，Lb=31.7 cm，代入(3)式可以求出，D=3.4 m，εm=2.3。反演计算出来的结果与先前假定取值(D=3 m，εm=2.9)存在部分偏差，初步分析原因包含以下两方面：(1)由于软件仿真精度的问题；(2)计算模型中没有考虑电磁波在介质中传播波形的形变。

图9 双天线时延法仿真结果

Fig.9 The result of the simulation of the signal-delay measurement with the dual-antenna receiver

图10 扣除地面反射波后的A、B天线接收波形

Fig.10 The result of the simulated signals of the signal-delay measurement with the dual-antenna receiver corrected for the ground echo

2.3 结果分析

利用标定件标定法计算月壤相对介电常数时，通过不同介质对电磁波反射的回波信号幅度差异反演月壤的介电常数，反演精度较高，但是利用该方法需要已知的介电常数的介质在介质表面反射后雷达回波信号的强度。

利用双天线时延法计算月壤相对介电常数时，通过同一个电磁波信号到达介质分界面后反射回来，被两个天线分别接收，两个天线接收存在时延差，利用该时延差可以求出月壤的厚度及相对介电常数。通过2.2节中的仿真结果，发现计算结果与假定值存在误差。这是由于该方法需要精准地记录电磁波到达的时间，两个天线本身距离较近，接收的时间差值较小，无论数值推导还是结合软件仿真，都必须保留很高的精度，否则对计算结果的影响还是存在的。另外电磁波在介质中传播时，电磁波本身波形的形状会有所改变，因此在波形上找出电磁波到达天线的时间时，存在偏差，这也是导致计算结果不一致的原因。

本文利用两种计算方法在计算介电常数时，同样存在局限性。标定件标定法，需要精确地知道相对介电常数介质的电磁波反射信号强度，并且需要在同一空间环境及雷达工作状态下，有了这个前提数据，才能跟雷达实测数据对比，进而求出月壤的介电常数；同时计算出来的相对介电常数为月壤表面值，无法计算月壤深层的相对介电常数。双天线时延法，可以同时计算出月壤的厚度及月壤的相对介电常数，但是只是适用于均匀的月壤介质并具有单一的分层模型，对于复杂的内部结构月壤分层，在雷达回波信号上由于内部复杂的结构会带来多次反射，以至于无法准确判断介质与下一层介质分界面的位置处的时延值，没有这个时延值，就无法代入公式进行计算，故利用该方法对于复杂分层情况及非均匀介质的计算实现上存在难度。

3 结 论

本文给出了两种计算月壤相对介电常数的方法，通过模型仿真验证了方法的有效性，并通过对仿真结果分析指出了两种计算方法的局限性及存在的问题，本文的研究工作有助于结合嫦娥三号雷达数据进行月壤介电常数的反演，最终为测月雷达数据的解译提供重要的技术支持。

[1] Yamaji A, Sasaki S, Yamaguchi Y, et al. Lunar tectonics and its implications for the origin and evolution of the moon[M]// The Memoirs of the Geological Society of Japan. 1998: 213-226.

[2] Fa W Z, Jin Y Q. A primary analysis of microwave brightness temperature of lunar surface from Chang-E 1 multi-channel radiometer observation and inversion of regolith layer thickness[J]. Icarus, 2010, 207(2): 605-615.

[3] Strangway D W, Pearce G W, Olhoeft G R. Magnetic and dielectric properties of lunar samples[C]// Pomeroy J H, Hubbard N J. The Soviet-American Conference on Cosmochemistry of the Moon and Planets. 1997: 417-433.

[4] Shkuratov Y G, Bondarenko N V. Regolith layer thickness mapping of the Moon by radar and optical data[J]. Icarus , 2001, 149(2): 329-338.

[5] Kobayashi T, Kim J H, Lee S R, et al. Simultaneous observation of Lunar Radar Sounder and Laser Altimeter of Kaguya for lunar regolith layer thickness estimate[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(3): 435-439.

[6] Fa W Z, Wieczorek M A. Regolith thickness over the lunar nearside: results from Earth-based 70-cm Arecibo radar observations[J]. Icarus, 2012, 218(2): 771-787.

[7] 欧阳自远. 月球科学概论[M]. 北京: 中国宇航出版社, 2005.

[8] Olhoeft G R, Strangway D W. Dielectrical properties of the first 100 meters of the moon[J]. Earth and Planetary Science Letters, 1975, 24(3): 394-404.

[9] 曾昭发, 刘四新, 冯晅, 等. 探地雷达原理与应用[M]. 北京: 电子工业出版社, 2010.

Studies and Simulations of Inversion Measurement of the RelativePermittivity of the Lunar Regolith Based on the LunarPenetrating Radar of the Chang’E-3

Xing Shuguo1,2, Su Yan1

(1. Natinal Astronomical Observatories, Chinese Academy of Sciences, Beijing, 100012, China, Email: xingsg@nao.cas.cn;2. Graduate University of Chinese Academy of Sciences, Beijng 100049, China)

The Chang’E-3 lunar probe was launched on December 2, 2013 and successfully landed on the moon. One of its important scientific payloads, the Lunar Penetrating Radar (LPR), is equipped on the lunar rover (Yutu) released by the Chang’E-3. The LPR has accomplished a first-ever on-spot radar survey of the lunar surface. In this paper we introduce the calibration method and the method of signal-delay measurement with the LPR dual-antenna receiver to measure the relative permittivity of the lunar regolith. The methods are based on the detection principle of the LPR, Using simulations we have verified the validity of the two methods. We also discuss the limitations of the two methods in the paper. Our work should serve as important basis for research of dielectric properties of the lunar subsurface based on LPR data.

Radio astronomy; Lunar Penetrating Radar; Relative Permittivity; Moon

国家自然科学基金 (11173038) 资助.

2014-08-02；修定日期：2014-09-02 作者简介：邢树果，男，博士. 研究方向：天文技术与方法. Email: xingsg@nao.cas.cn

T161

A

1672-7673(2015)03-0306-06