单级旋转倒立摆运动控制研究

刘二林，姜香菊

LIU Er-lin1, JIANG Xiang-ju2

（1.兰州交通大学 机电工程学院，兰州 730070；2.兰州交通大学 自动化与电气工程学院，兰州 730070）

0 引言

倒立摆系统与两轮自平衡机器人一样，均与火箭飞行，两足机器人行走有很大的相似性。对倒立摆系统进行理论研究有理论和实践意义。人们可以通过对倒立摆系统的控制来检验所使用的控制方法对不稳定系统的控制能力。倒立摆的种类很多，有直线倒立摆、旋转倒立摆、平面倒立摆等。旋转倒立摆是三种形式的倒立摆中结构较简单的一种，但是其受力分析较其他两种复杂，具有不稳定性及非线性，对控制算法有更高的要求。旋转倒立摆的运动控制是指旋转倒立摆在倒立状态下，能按照要求稳定的向某一方向匀速旋转，这种运行模式类似于两足机器人的行走过程，可以将这种控制研究作为对两足机器人运行的模拟研究[1,2]。

PID控制器是自动控制领域出现最早的控制方法，其应用非常广泛，有着较强的实用性及通用型，在文献[3]、[4]中，作者都采用了PID对倒立摆状态进行控制。文献[5]中，作者则针对直线倒立摆，用PD、PI和PID实现了对倒立摆的平衡控制，并对控制效果进行了对比。线性二次型最优控制器LQR (linear quadratic regulator)又称为线性二次型调节器。LQR的控制对象为线性系统，常用于求解动态系统的最优问题。在文献[6]至文献[9]中，均采用LQR来实现对倒立摆或者两轮直立车的平衡控制。文献[10]中则是利用LQR实现对两轮平衡车的状态保持控制，然后用另一种控制模式对平衡车进行运动控制。

本文中首先设计了一个一级旋转倒立摆，然后根据实际情况建立了倒立摆的数学模型，并在平衡点附近给出系统的线性化状态方程。分别使用双PID控制算法和LQR状态跟随控制算法来实现其运动控制。并通过仿真及实测来检验其优劣。

1 旋转倒立摆系统的数学模型

1.1 旋转倒立摆基本结构

旋转倒立摆主要由倒立摆支撑机架、电机、减速装置、摆杆、旋臂、1024线位置式编码器、BT7960构成的H桥电路及微控制器芯片组成。倒立实物图如图1所示。

图1 倒立摆结构

在图1中，旋转倒立摆的旋臂与减速器的输出轴联接，减速器由直流电机驱动，编码器1的齿轮与直流电机主轴齿轮啮合。通过获取编码器1的角度和角速度可以计算出旋臂的角度和角速度。编码器2安装在旋臂末端，且编码器2的旋转轴与旋臂的主轴平行；摆杆安装在编码器2的旋转轴上，摆杆轴线与编码器旋转轴垂直。系统中，旋臂只能以减速器动力输出轴为圆心做水平旋转，摆杆只能以编码器2旋转轴为圆心在旋臂末端旋转轨迹的切面上做竖直旋转[11,12]。

1.2 旋转倒立摆数学模型

对倒立摆进行受力分析，建立广义坐标系。系统的简化模型如图2所示。利用拉格朗日方程建立系统的运动学微分方程[1,2,4]。

由图2可知，系统中摆杆与旋臂各有一个自由度，所以，可以取α和θ为广义坐标。则倒立摆系统的动能由四部分组成。

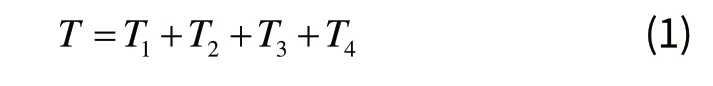
其中，T1为旋臂的转动动能，T2为摆杆的转动动能，T3为摆杆沿X轴方向运动的动能，T4为摆杆沿Y轴方向运动的动能，

因为α→0，所以sinα→0，cosα→1，将式1各项进行计算合并，并且对其进行线性化处理可得：

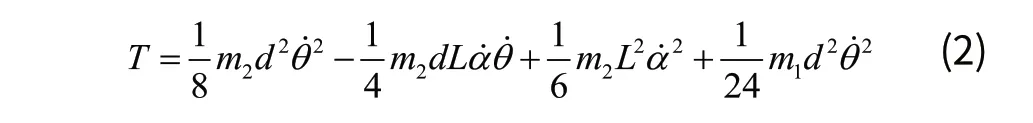
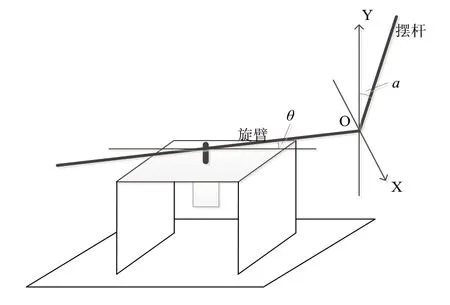
图2 系统简化模型

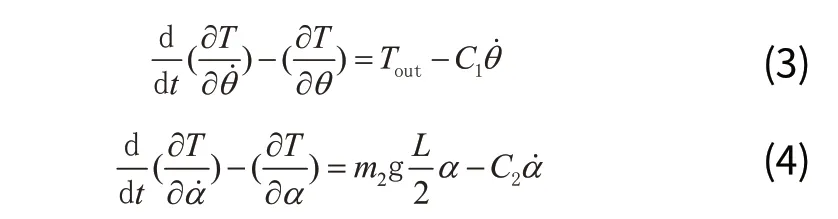
由式(3)可得：

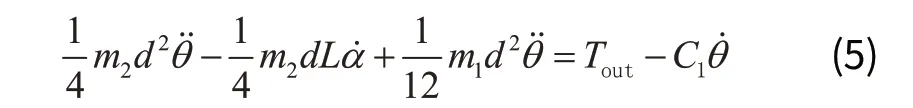
式(5)中，Tout为电机输出扭矩，由式(4)可得：

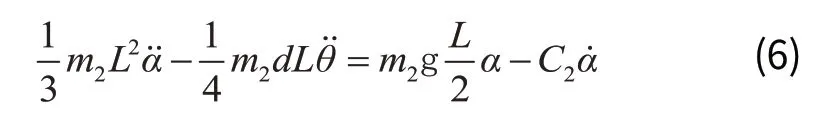
将式(4)、式(5)联立组成方程组，得到倒立摆系统线性化状态方程

以上各式中参数的物理意义、数值及单位如表1所示。

2 倒立摆的运动控制

2.1 基于双PID的运动控制

因为采用了绝对式编码器来进行角度检测，所以在获取角度和角速度时系统不存在滞后和噪音。建立系统的传递函数，利用李雅谱诺夫稳定性理论进行分析可知，系统可控。用双PID控制器可以使系统稳定运动。控制器中有两路PID，PID1控制倒立摆摆杆的状态（这时取KI=0）；PID2控制旋臂的运动（PID的极性为负）；控制器的两个输入量分别是倒立摆摆杆旋臂角速度θ˙，倒立摆摆杆角度α。同时，要使系统稳定，则要保证PID2的KP不能太大，PID2的输出要小于PID1的输出。旋转倒立摆双PID运动控制仿真图如图3所示。

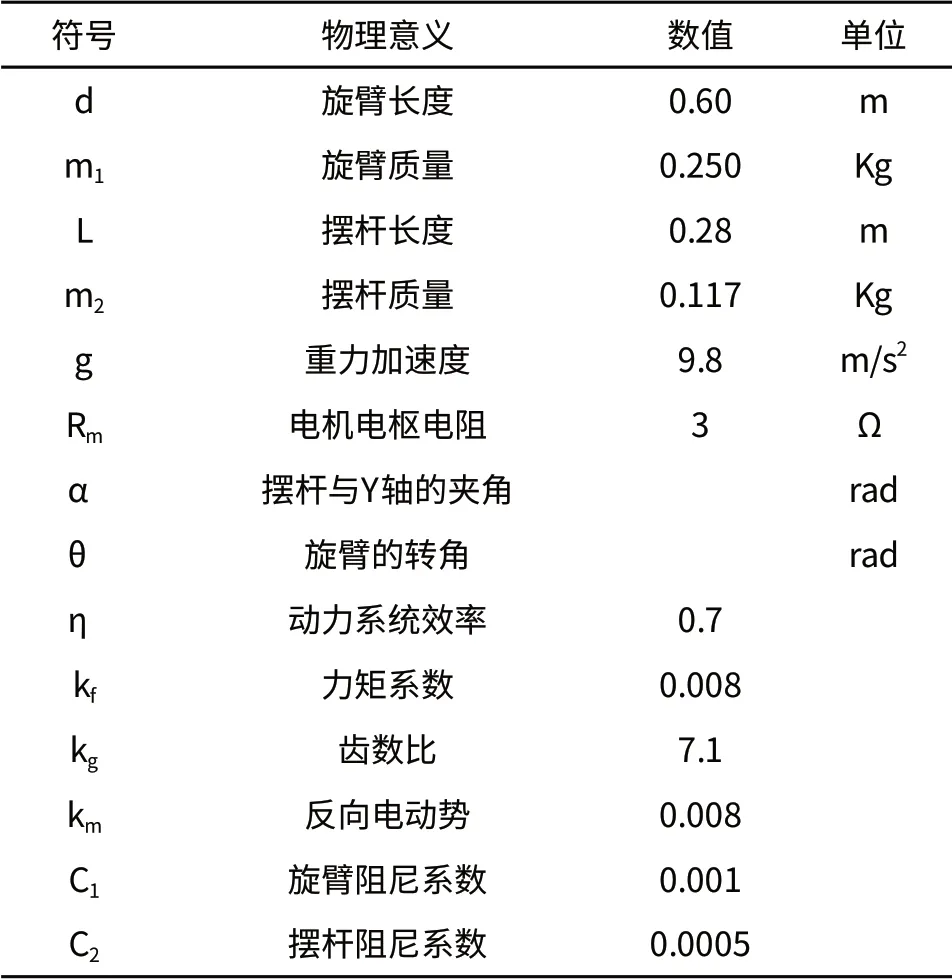
表1 状态方程中各参数列表

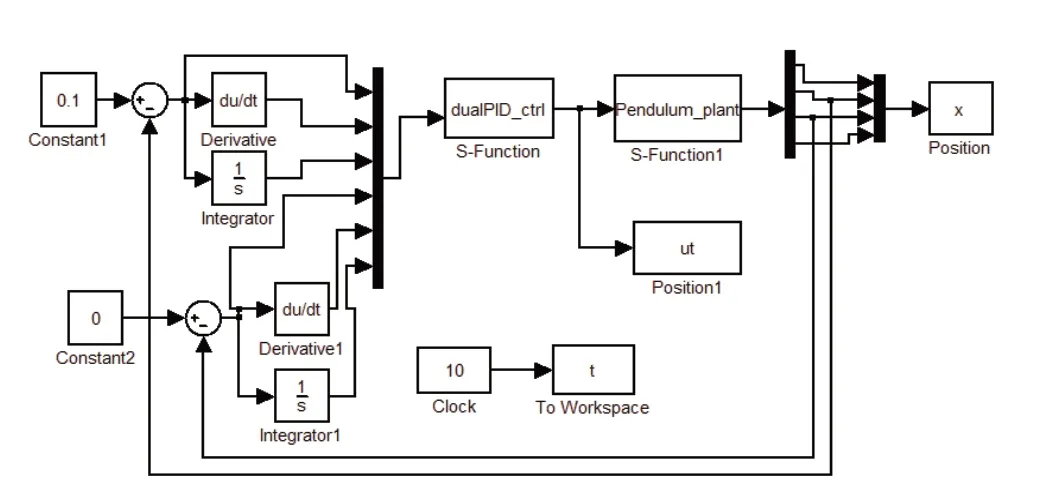
图3 双PID运动控制Simulink仿真程序

在M文件中，取KP1=100，KD1=20，KI1=0；KP2=2.0，KD2=0.08，KI2=0.0185。仿真结果如图4所示。在图4中可以看出，倒立摆摆杆在3s以内完成直立，旋臂速度在4s以内达到设定值，旋臂按照设定要求在倒立摆倒立的情况下向设定方向稳定运动。

在仿真过程中，KP1决定了系统的响应速度，KP1越大，倒立摆响应速度越快；KD1决定了系统是否震荡（相当于倒立摆的阻尼系数），如果KD1变小，则系统会产生震荡。KP2决定了旋臂速度的响应时间，但如果KP2取值太大，则倒立摆系统不稳定；KD2可以改善系统的超调，但是KD2太大也会使系统的抗干扰能力变差，甚至发散；KI2的作用是减小静差，但是KI2太大会使系统震荡。双PID旋转倒立摆运动控制调节参数较为麻烦。

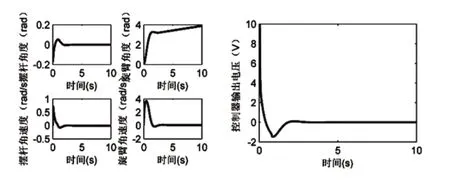
图4 双PID控制仿真结果

2.2 基于LQR的运动控制

根据现代控制理论，设状态反馈控制律的形式为：u=-K×xu。在本模型中，由于x是四维状态变量；所以，K=[k1,k2,k3,k4] ，K的取值要满足使线性二次型最优性能指标J最小。

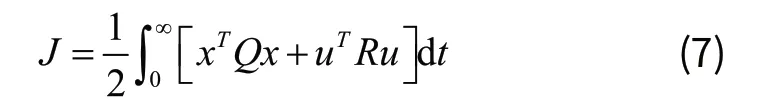
其中u不受限制，Q是半正定常数矩阵，R为正定常数矩阵。求得状态反馈矩阵K=-R-1BTP，P为满足代数Riccati方程的唯一正定对称解。

代数方程为：

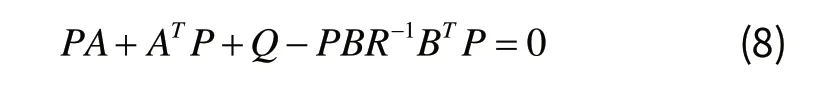
Q和R确定后，利用MATLAB便可以求得状态反馈矩阵K，调整对角矩阵Q中的参数，也即各输入量的权重，便可以在仿真时得到期望的效果。该LQR最优控制可以使系统从任意初始状态返回到平衡状态（0状态）[6～10]。

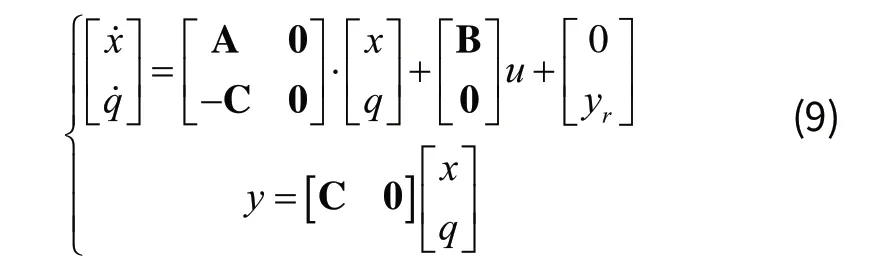
其中A、B、C同前面倒立摆数学模型中的A，B，C。对增广系统的可控性进行分析，系统能控。设计基于LQR的状态跟随控制器如图5所示。

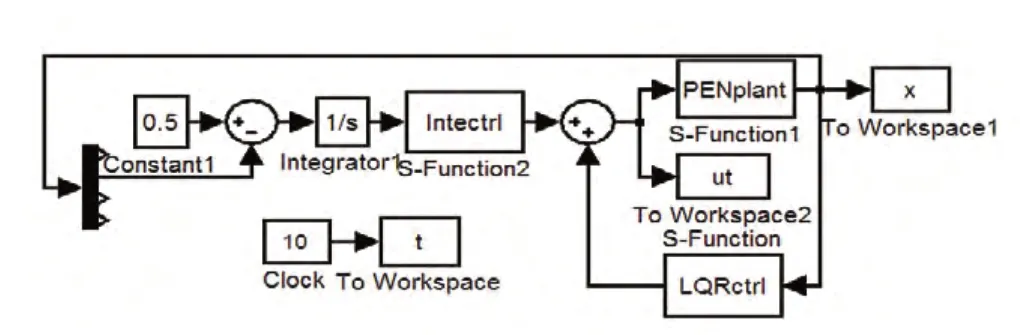
图5 LQR状态跟随Simulink仿真程序

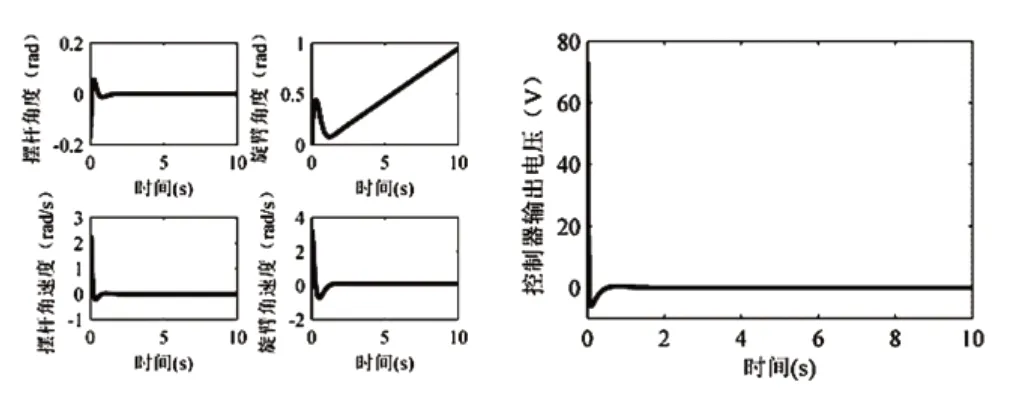
图6 LQR控制仿真结果

2.3 控制方式效果对比

设定不同的参数，控制效果对比结果如表2所示。

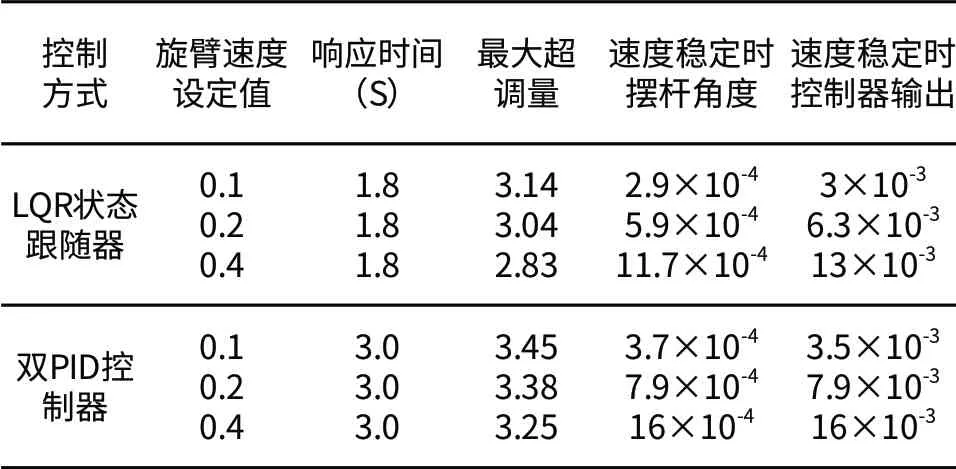
表2 两种控制方式效果对比

通过对比仿真结果可以看出，LQR状态跟随器控制效果明显优于双PID控制器。控制结果可以明显看出，LQR状态跟随控制器的超调小，响应速度快；同时，LQR参数调整方便。在仿真实验中还验证了LQR状态跟随控制器鲁棒性好。而双PID控制的优点在实现方便，不过分依赖于所建立的数学模型。

最后，将MATLAB计算出的K值及其相关算法移植到微控制器中对实物进行了控制，经过对参数进行进一步的调整，实际运行效果验证了仿真结果的正确性。

3 创新点

设计的创新点在于研究了单级旋转倒立摆的运动控制问题。在利用拉格朗日方程建立倒立摆系统的线性化状态方程后，利用双PID控制器和LQR状态跟随控制器对模型进行了控制。单级旋转倒立摆与两轮直立机器人的运动有极大相似性，论文通过LQR状态跟随控制器对旋转倒立摆进行了运动控制，控制仿真结果及实测结果证明：LQR状态跟随控制器不经过解耦也可以很好控制不稳定体的运动，并且响应速度快，超调小，系统鲁棒性好。

[1] 吴爱国,张小明,张钊.基于Lagrange方程建模的单级旋转倒立摆控制[J].中国工程科学,2005,7(10):11-15.

[2] S.Awtar,N.King,T.Allen,I.Bang,M.Hanan,D.Skidmore,K.Craig. Inverted pendulum systems: rotary and arm-driven-a mechatronic system design case study[J].Mechatronics,2002,(12):357-370.

[3] 曹敏,徐凌桦.单神经元PID算法在倒立摆控制系统中的应用[J].微计算机信息,2009,25(1-1):70-71.

[4] 江晨,王富东.旋转式倒立摆系统的算法研究及仿真[J].工业控制计算机,2010,23(5):54-56.

[5] 杨世勇,徐莉苹,王培进.单级倒立摆的PID控制研究[J].控制工程,2007,14(增刊):23-24,53.

[6] 邢景虎,陈其工,江明.基于LQR的直线一级倒立摆最优控制系统研究[J].工业仪表与自动化装置,2007(6):3-5.

[7] 张金学,掌明.两轮自平衡机器人的LQR实时平衡控制[J].自动化与仪表,2013(5):5-9.

[8] 谌海云,杜振华,邹宁波,石明江.多种群遗传算法的倒立摆LQR控制器设计[J].控制工程,2014,21(3):391-394.

[9] 于海洋.基于LQR理论的直线单级倒立摆PID控制仿真研究[J].佳木斯大学学报(自然科学版),2010,28(6):821-823.

[10] 阮晓钢,赵建伟.基于PWM伺服控制及LQR的两轮自平衡移动机器人[J].控制工程,2009,16(3):363-366.

[11] 张朝阳,魏晓赟,王少峰.基于52单片机的旋转倒立摆的研究和与设计[J].廊坊师范学院学报(自然科学版),2014,14(4):49-52.

[12] Du Gaixin,Huang Nanchen, Wu Gang. The rotational invertedpendulum based on DSP controller[A].Proc of the 4th World Congress on Intelligent Control and Automation[C].China Shanghai,2002,7(4):3101-3105.