拟周期激励下非线性半车模型的混沌振动研究

杨智勇， 梁 山， 周 桐

(1.重庆工程职业技术学院 信息工程学院， 重庆 402260； 2.重庆大学 自动化学院， 重庆 400044)

拟周期激励下非线性半车模型的混沌振动研究

杨智勇1,2， 梁 山1， 周 桐1

(1.重庆工程职业技术学院 信息工程学院， 重庆 402260； 2.重庆大学 自动化学院， 重庆 400044)

为了克服单一频率路面激励下车辆悬架模型不能真实反映实际车辆的非线性动力学特性问题，建立了双频拟周期动态路面激励函数，并构建了4自由度非线性1/2车辆悬架模型.运用庞加莱图、相位图，功率谱密度分析了车辆4自由度非线性半主动悬架模型通过凹凸不平路面时的动力学特性，得到了系统发生混沌振动时的激励振幅和振动特性，即车辆通过凹凸不平路面时的振动特性为:拟周期→过渡态→混沌态.同时通过调整弹簧刚度系数，有效抑制了混沌振动的发生.研究结果表明:双频拟周期激励下的4自由度非线性半主动悬架模型模拟更能接近实际情况，这有助于汽车悬架的设计和路面铺装设计.

拟周期；非线性车辆；半主动悬架；混动振动

0 引言

由于车辆系统中悬架、轮胎、弹簧、阻尼元件存在非线性特性，因此当车辆通过凹凸不平的路面时，路面激励可能导致车辆内部发生复杂的非线性动力学现象，如分岔现象、混沌振动等[1-2].这些非线性现象可能会导致车辆振动加剧，增大系统噪声，破坏周边环境，造成元器件磨损和道路早期疲劳损害，甚至威胁乘车舒适性和行车安全[3-4].因此对车辆通过凹凸不平路面产生混沌振动的机理和抑制混沌振动的方法开展研究，对提高驾乘人员舒适性具有重要意义.

近年来，对汽车非线性悬架的混沌振动的机理研究，特别对路面不平度激励下非线性车辆悬架系统的混沌振动的研究已越来越受到人们的关注[1-7].但是由于非线性系统的复杂性，目前模型多是简单的单自由度1/4车辆模型和两自由度1/4车辆模型.1/4车辆模型是一种极其简化的模型，它将汽车简化为一个车轮支撑的振动系统，只能研究车辆在垂直方向的振动，忽略了真实悬架系统很多重要的振动特性，很难提供足够反映悬架系统和车体的实际动态特性的信息，不能代表真实的车辆系统悬架特性[3-6].而4自由度1/2车辆模型是一种相对接近实际悬架系统的模型，它可用于研究车身的垂直运动和俯仰运动以及前后2车轮的垂直运动，并可研究前后两轮激励输入相位差对系统动态特性的影响.由于随机路谱表示的路面激励不便于理论研究，因此，路面激励模型多以单一频率或双频的正弦或余弦来近似模拟路面激励，讨论路面位移激励对系统非线性特性的影响[1-2,7].但是单一的正弦频率很难真实地表示路面的真实激励.目前针对双频拟周期激励下多自由度非线性车辆悬架的混沌振动的研究还鲜见报道.鉴于以上问题，笔者采用双频正弦拟周期激励来表示凹凸不平的路面，以4自由度非线性半车模型为研究对象，研究非线性车辆在路面双频拟周期激励下的混沌振动.所谓拟周期是指当各个激励频率不可有理通约时称为拟周期[7].笔者首先建立了车辆悬架和路面激励模型，通过分析Poincaré截面图、相位图、功率谱等，验证了模型的合理性和系统存在混沌的可能性.

1 车辆模型及运动微分方程

为了得到更具有价值的车辆非线性动力学特性，笔者将车辆看成左右对称的结构，由此建立4自由度非线性半车悬架系统模型，其模型力学结构如图1所示[3-4].4自由度非线性半车模型能对前后车轮、车身垂直和俯仰方向的非线性运动作较为完备的研究，同时研究车辆前后轮激励的时间差对车辆悬架的影响，具有较强的理论研究价值.

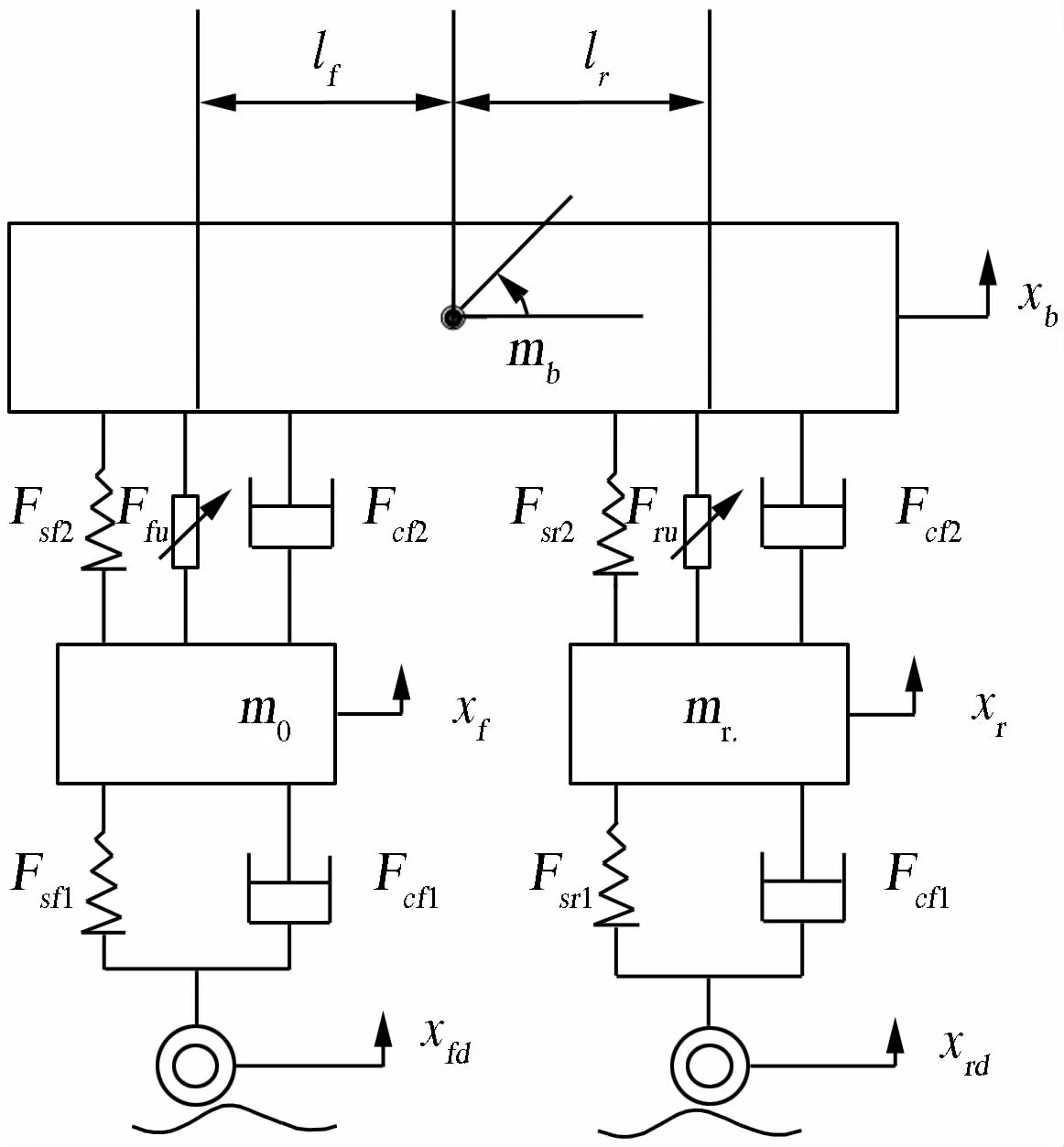
图1 4自由度非线性半主动半车悬架模型Fig.1 Non-linear 4-DOF half-active half-vehicle suspension model

在图1中,mb为车身质量；mf，mr为前后轮非簧载质量；xf为mf的垂直位移；xr为mr的垂直位移；xfd，xrd为前后轮受到的外部激励；Fsf1，Fsr1为前后轮悬架非线性阻尼力；Fsf2，Fsr2为前后非线性悬架弹簧力；Fcf1，Fcr1为前后非线性轮胎弹簧力；Fcf2，Fcr2为前后悬架非线性阻尼力；Ffu，Fru为前后悬架主动控制力.

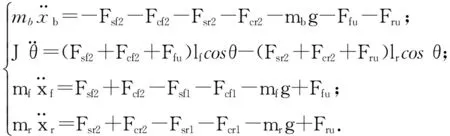
(1)

弹簧的非线性特性分别被表示为

Fsf1=100(nf1-1)kf1sgn(Δxf1)|Δxf1|nf1；

(2)

Fsr1=100(nr1-1)kr1sgn(Δxr1)|Δxr1|nr1；

(3)

Fsf2=100(nf2-1)kf2sgn(Δxf2)|Δxf2|nf2；

(4)

Fsr2=100(nr2-1)kr2sgn(Δxr2)|Δxr2|nr2.

(5)

其中，

Δxf1=xf-xfd-sf1；

(6)

Δxf2=xb-xf-sf2-lfsinθ；

(7)

Δxr1=xr-xrd-sr1；

(8)

Δxr2=xb-xr-sr2-lrsinθ.

(9)

式中:sf1和sr1分别表示前后车轮在无激励下的弹性形变; sf2和sr2分别表示前后悬架在无激励下的弹性形变;kf1和kr1分别表示前后轮胎的等效刚度；kf2和kr2分别表示前后悬架的等效刚度.

阻尼器的非线性特性被表示为[4-5]

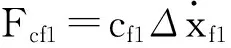
(10)

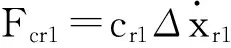
(11)

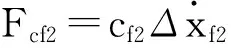
(12)

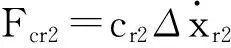
(13)

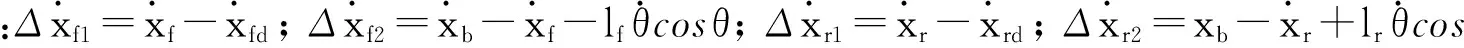
式中:cf1和cr1表示前后轮胎的非线性阻尼因子; cf2和cr2表示前后悬架的非线性阻尼因子，表示为

(14)

(15)

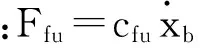
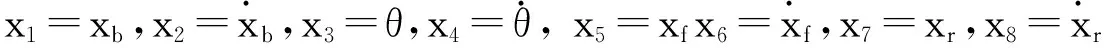
(16)

设mb前后轴承受的分质量，分别为mbf和mbr，可计算得

(17)

因此，车辆悬架垂直方向的静态状态方程可表示为

(18)

从式(18)可得

(19)

2 路面激励模型及车辆悬架混沌振动分析参数

笔者用双频正弦拟周期函数表示路面不平度激励，因此路面不平度可近似地用如下等式表示.

xfd=A1sinω1t+A2sinω2t ；

(20)

xrd=A1sin(w1t+α)+A2sin(w2t+α) .

(21)式中：A1和A2表示路面激励的振幅;ω1和ω2分别表示两个正弦激励的角频率;α表示激励对前后车辆的滞后延迟,α的值约等于(lf+lr)/v, lf和lr是前后车轮和车辆中心位置的距离.

由于系统非线性微分方程的存在，故可采用定步长4阶Runge-Kutta算法进行仿真研究.数值仿真的汽车模型参数见表1[4, 6].

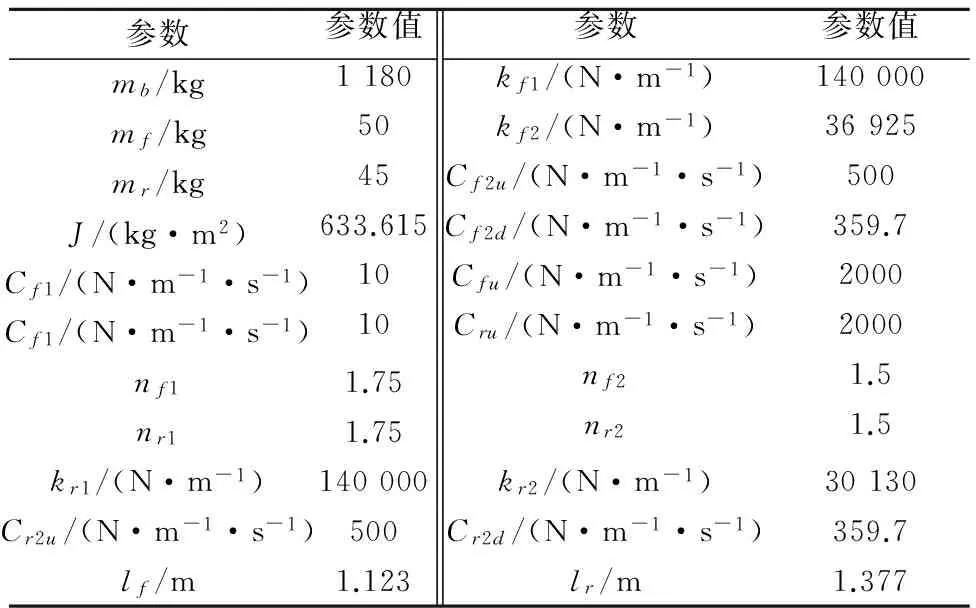
表1 数值仿真参数Tab.1 Parameters for numerical simulation

3 仿真分析

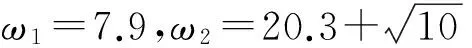
当A1=A2=0.004,nf1=nf2=1.75时，车辆的运动状态为拟周期，如图2所示.

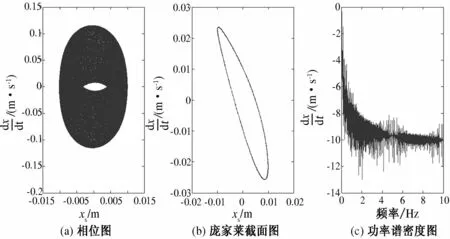
图2 拟周期运动Fig.2 Quasi periodic motion

当A1=A2=0.038,nf1=nf2=1.75时，拟周期环破裂，有进入混沌运动状态的趋势，笔者将此状态称为过渡运动态，如图3所示.

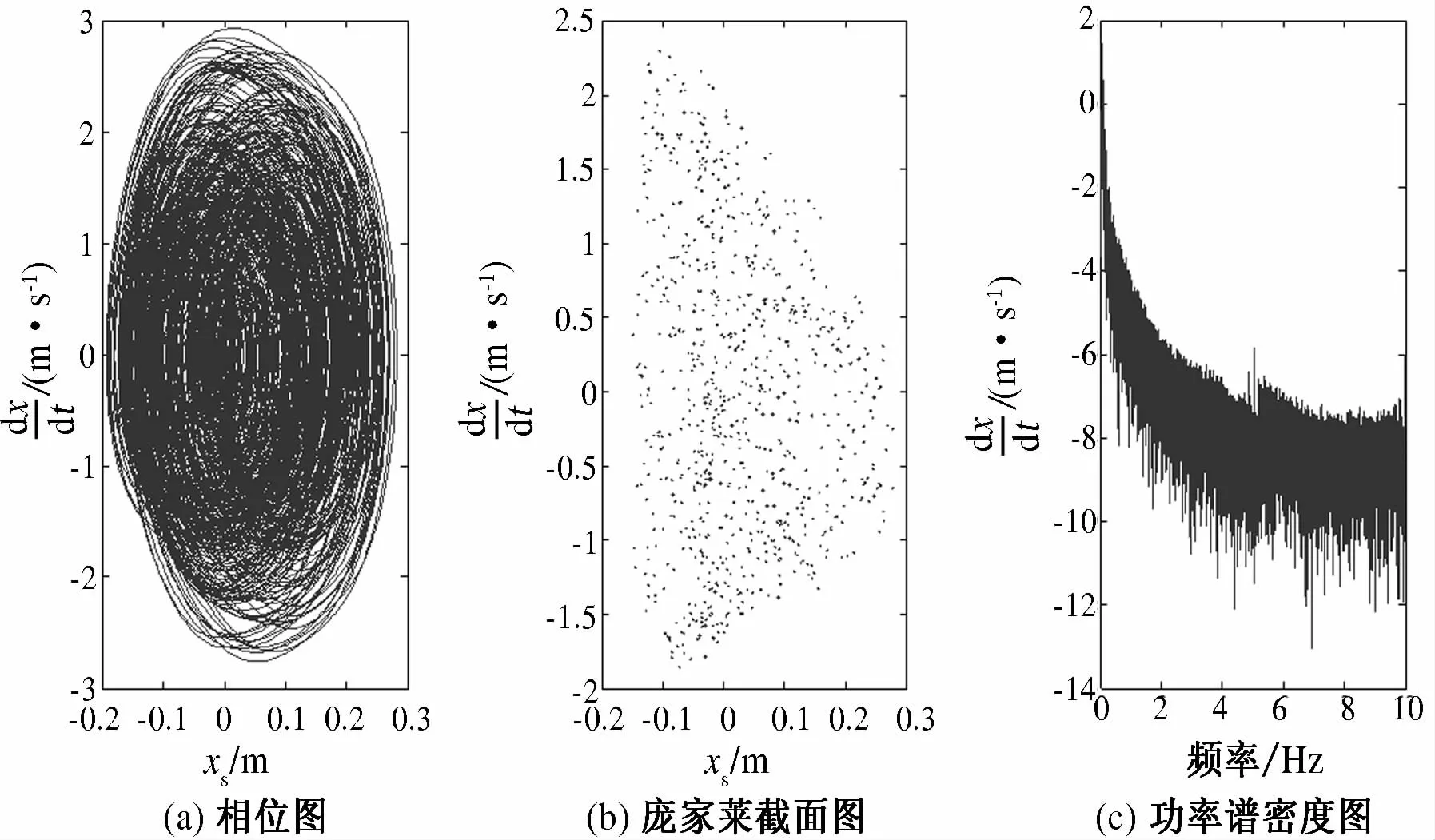
图3 过渡态运动Fig.3 The transition state of motion

当A1=A2=0.04,nf1=nf2=1.75时,系统运动从过渡态进入到混沌状态，如图4所示.

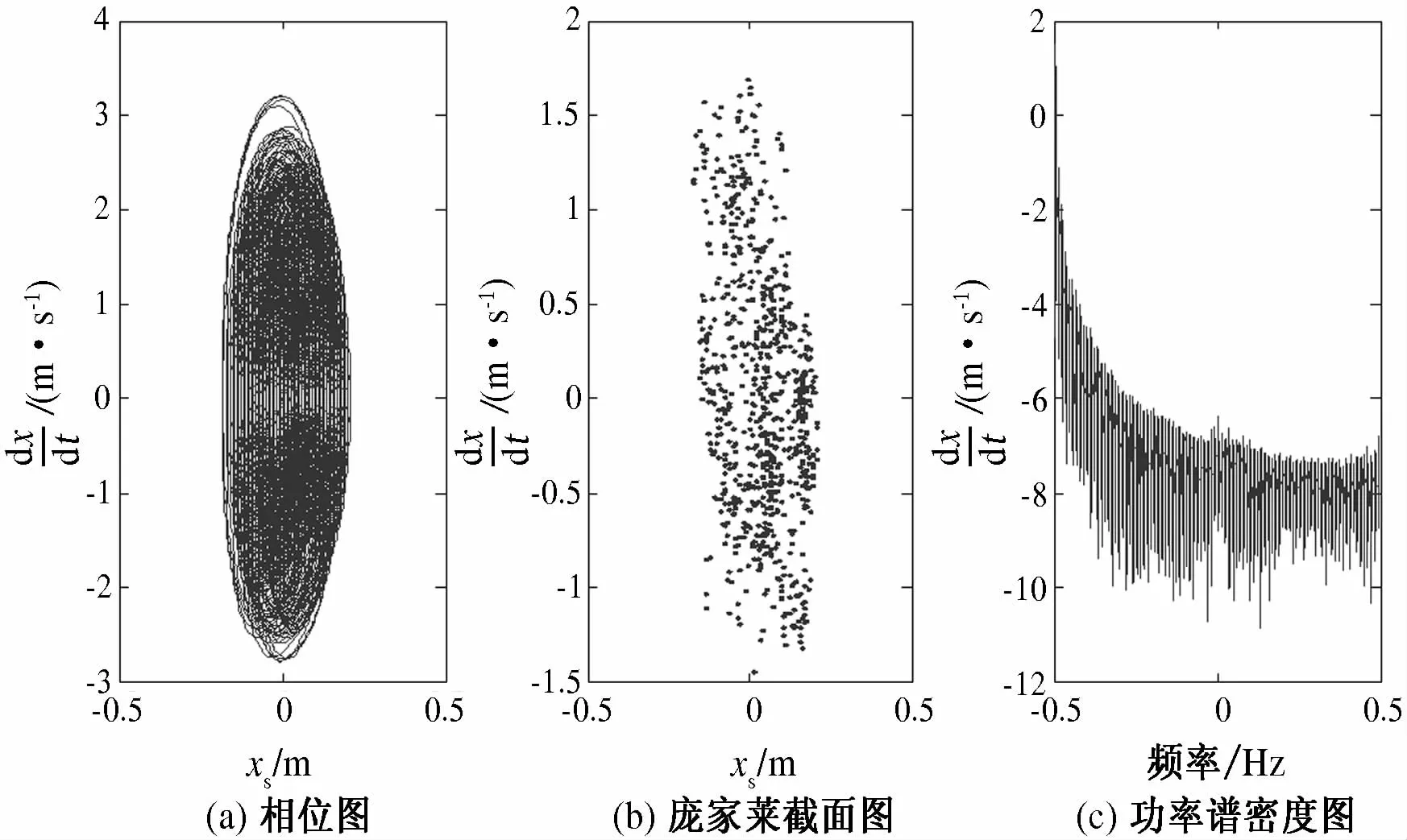
图4 混沌运动状态Fig.4 Chaotic motion

为了进一步研究引起车辆发生混沌振动的机理，为车辆悬架设计提供依据参考，论文通过调整车辆前后悬架弹簧刚度系数进行对比研究.悬架弹簧刚度系数nf1=nf2=1.25，路面激励振幅A分别为0.004，0.038，0.04时系统的运动特性如图5～7所示.

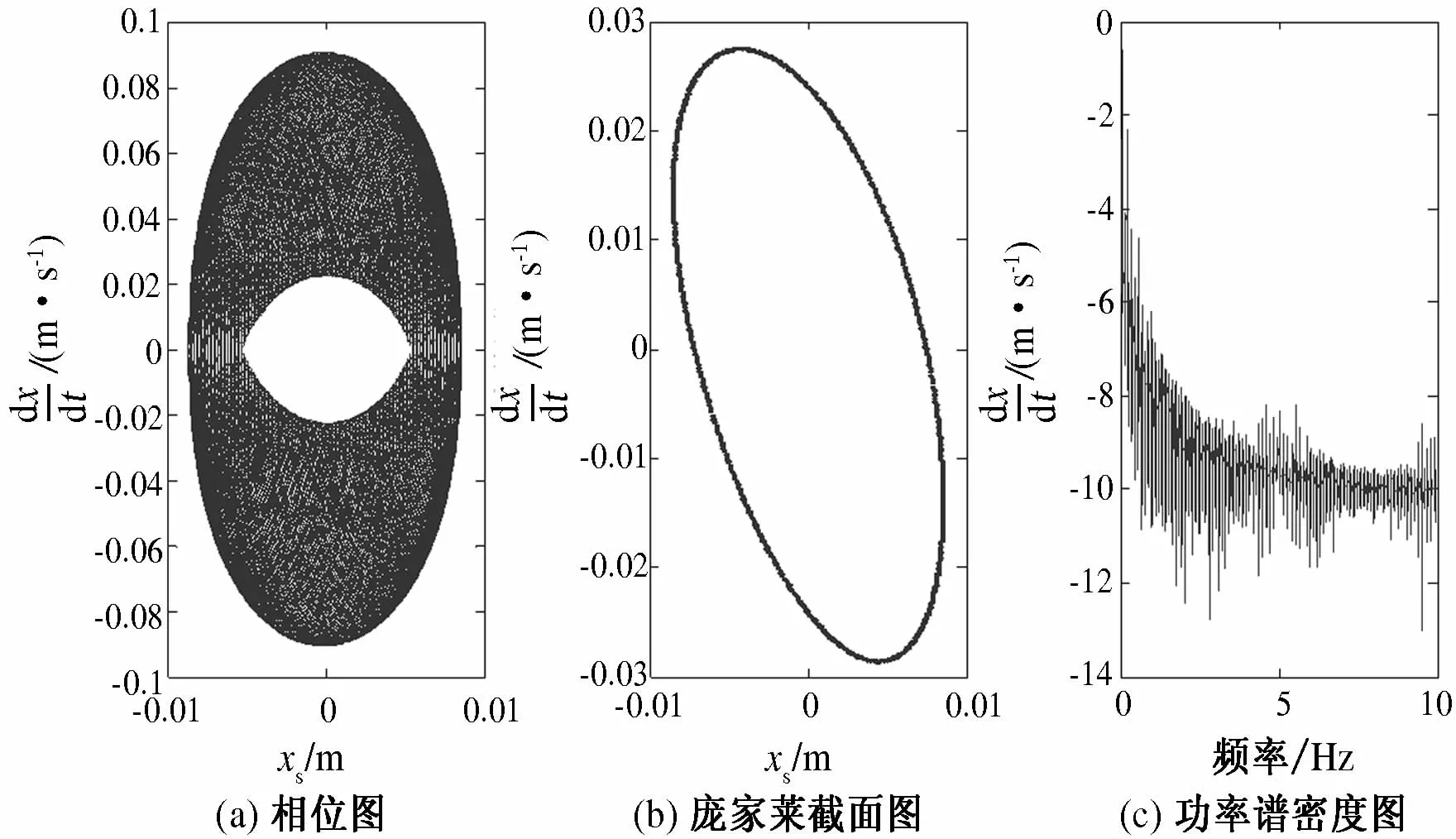
图5 拟周期运动Fig.5 Quasi periodic motion

在路面相同振幅激励下，通过将前后悬架弹簧刚度系数从1.75调整为1.25后，车辆悬架原先的过渡态和混沌态不再存在，而是做拟周期运动，这说明了可以通过调整车辆悬架弹簧的刚度系数来改变车辆的运动状态，提高乘坐舒适性和行车安全性.

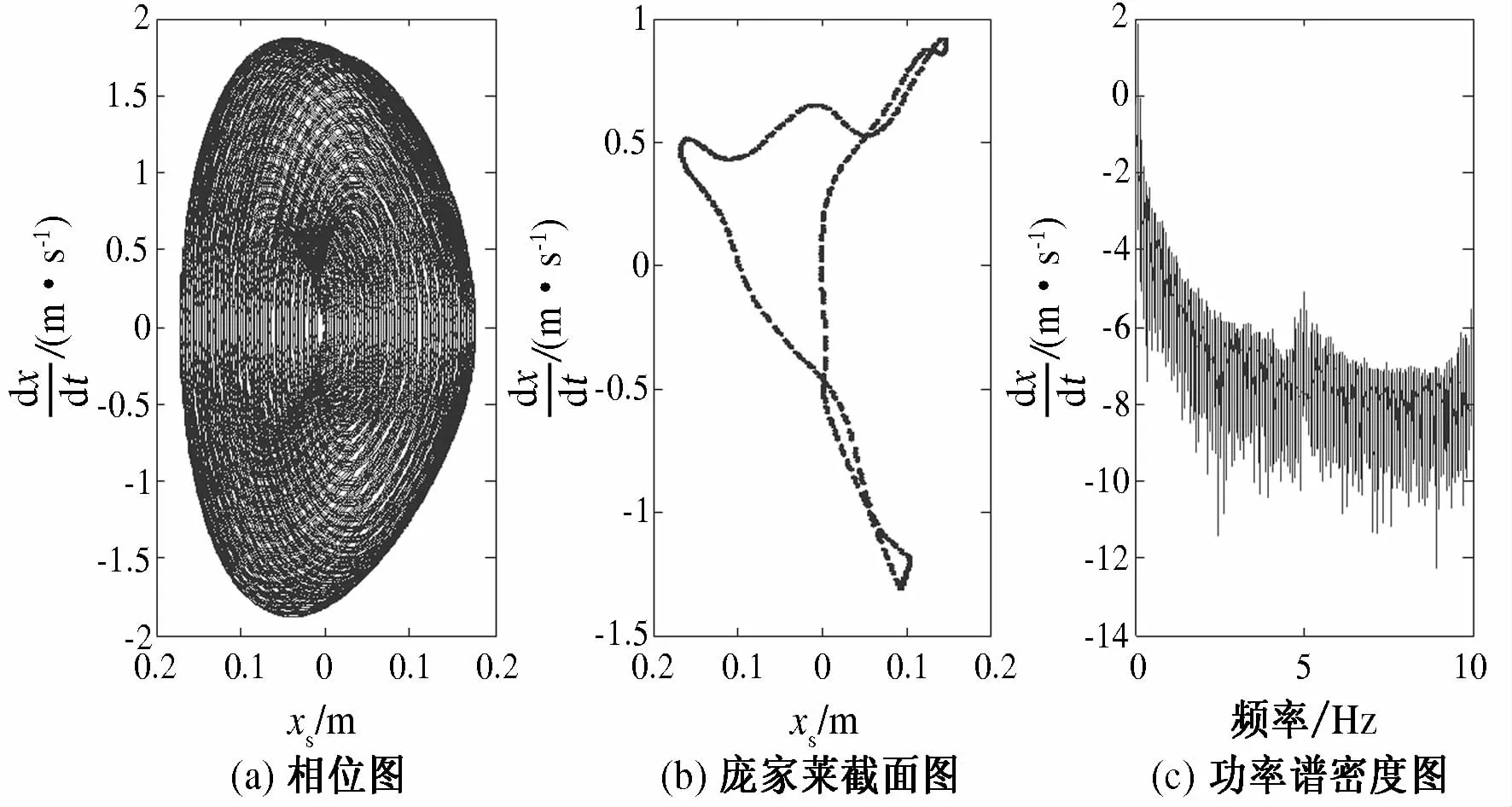
图6 拟周期运动Fig.6 Quasi periodic motion

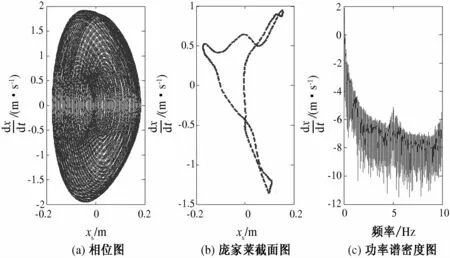
图7 拟周期运动Fig.7 Quasi periodic motion

4 结论

笔者采用数值仿真方法分析了4自由度1/2非线性悬架模型在双频拟周期激励下的混沌振动.采用庞加莱图、相位图和功率谱密度证实了系统发生混沌的可能，同时获得了系统发生混沌振动时激励的振幅.仿真结果揭示了车辆悬架系统通过凹凸不平路面时的振动特性为拟周期→过渡态→混沌态.同时在路面激励振幅不变的情况下，通过调整车辆前后悬架弹簧刚度系数，有效改变了车辆悬架的运动状态:车辆从混沌运动状态转变到了拟周期运动状态.结果验证了可以通过调整悬架弹簧系数来有效避免混沌运动产生.研究结果对车辆悬架设计和路面铺装具有重要参考意义.下一步将通过理论方法对系统发生混沌的可能性和振动特性进行推导，通过对比分析理论推导和仿真分析结果，为悬架的动力学特性设计和道路路面铺装提供理论依据.

[1] LIANG Shan, LI Cong-gang, ZHU Qin. The influence of parameters of consecutive speed control humps on the chaotic vibration of a 2-DOF nonlinear vehicle model[J]. Journal of Vibroengineering, 2011, 13(3)： 406-413.

[2] LIU Fei，LIANG Shan，ZHU Qin，et al. Effects of the consecutive speed humps on chaotic vibration of a nonlinear vehicle model[J]. ICIC Express Letters，2010，4(5)：1657-1664.

[3] YANG Zhi-yong，LIANG Shan，ZHU Qin. Chaos of a nonlinear half-vehicles suspension system excited by the consecutive speed-control humps[J]. ICIC Express Letters，2013，7(11)：3163-3168.

[4] ZHU Qin，ISHITOBI M. Chaos and bifurcations in a nonlinear vehicle model[J]. Journal of Sound and Vibration，2004,275(3)：1136-1146.

[5] 王威，李瑰贤，宋玉玲. 四轮激励含相位差的汽车高维非线性超混沌动力学特性研究[J]. 振动与冲击，2009，28(3)：102-202.

[6] ZHU Qin, ISHITOBI M. Chaotic vibration of a nonlinear full-vehicle model[J]. Journal of Solids and Structures ，2006,43(3)：747-759.

[7] 李韶华，杨绍普. 拟周期激励下滞后非线性汽车悬架的混沌[J]. 振动与冲击，2003，22(3)：61-65.

Research on Chaotic Vibration Characteristics of Nonlinear Half Vehicle Model under Quasi-Periodic Excitation

YANG Zhi-yong1,2， LIANG Shan1，ZHOU Tong1

(1.College of Information Engineering, Chongqing Institute of Engineering, Chongqing 402260, China; 2.College of Automation, Chongqing University, Chongqing 400044, China)

To overcome the problem that the vehicle suspension model of the single periodic excitation road does not truly reflect the nonlinear dynamics characteristics of the actual vehicle, the paper establishes a quasi-periodic dynamic road excitation function, and builds a four-degree of freedom nonlinear half vehicle suspension model. Using the Poincaré map, phase diagram, power spectral density to analyse the nonlinear dynamics characteristics of the four degrees of freedom semi-active vehicle suspension model on uneven road surface, we obtain the amplitude of chaotic vibration and its vibration characteristics which is quasi-periodic → transition state → chaotic state as the vehicle through uneven road surface. At the same time, the occurrence of chaotic vibration can be inhibited effectively by adjusting the spring stiffness coefficient. The results show that the simulations of the four degrees of freedom nonlinear semi-active suspension model under dual-frequency quasi-periodic excitation is more closer to the real situation, which helps the design of vehicle suspension and pavement.

quasi-periodic； nonlinear vehicle； semi-active suspension； chaotic vibration

2014-08-17；

2014-11-10

中央高校基本科研业务基金项目(CDJXS12170002)；重庆市科技项目基金资助项目(KJ112002)

杨智勇(1979-)，男，重庆忠县人，重庆工程职业技术学院副教授，博士，主要从事非线性控制理论研究，E-mail:yzy023@aliyun.com.

1671-6833(2015)01-0110-04

TP391.9

A

10.3969/j.issn.1671-6833.2015.01.026