电力电缆循环加热试验中热力学工态研究

王光斌，杨海马,2，杨 晖，陆 崚，金智勇，马 生，黄影平

(1.上海理工大学 光电信息与计算机工程学院， 上海 200093； 2.中国科学院 上海技术物理研究所，上海 200083； 3.上海蓝波高电压技术设备有限公司， 上海 200245)

电力电缆循环加热试验中热力学工态研究

王光斌1，杨海马1,2，杨 晖1，陆 崚3，金智勇3，马 生1，黄影平1

(1.上海理工大学 光电信息与计算机工程学院， 上海 200093； 2.中国科学院 上海技术物理研究所，上海 200083； 3.上海蓝波高电压技术设备有限公司， 上海 200245)

为研究电力电缆热循环载流量试验中电缆的温升特性，以及介质损耗和环境温度对电力电缆温升的影响，完善了空气中电缆集中参数等效热路模型，建立了暂态下对导体损耗、介质损耗和环境温度进行实时修正的热流微分方程.仿真计算给电缆施加恒定电流时电缆导体、金属套的温升，介质损耗对温度的工态影响，电缆热循环载流量试验中电缆各层的暂态温升和自然冷却曲线，并与实际试验所测得的温升曲线进行拟合验证.研究结果表明，高压电力电缆热循环试验中，介质损耗对电缆温升影响较大，试验中需要对导体损耗、介质损耗和环境温度进行实时修正.

电力电缆；介质损耗；热流微分方程；温升特性

0 引言

为保障电力电缆的输送能力和电力电缆设施的安全[1]，对电力电缆载流量和温升特性的试验和研究显得非常重要.目前对电缆的相关试验一般按IEC62067:2006[2]进行.虽然电缆额定载流量和温升计算已十分完善，但对于特殊结构或特殊敷设条件下的电缆仍提倡试验解决.例如热循环试验，一般采用导体电流加热的方式，每个周期应至少加热8 h，加热至规定温度范围保持2 h，随后至少自然冷却16 h.电缆温升试验耗费高、周期长，实验室环境单一，难以模拟室外电缆运行环境，从而影响了电缆温升特性研究的准确性，不利于电缆研发制造.一些仿真模型没有充分考虑外部环境对温升的实时影响[3]，忽略了高压电力电缆的介质损耗，对电缆的实际使用留下了安全隐患，因此有必要模拟电缆实际运行环境，建立一个较为完善，实时考虑外部环境温度和介质损耗的热路模型，从理论上研究电缆的温升特性以及介质损耗和电阻损耗对温升的影响，并以实验加以验证，为不同物理参数的电缆试验提供参考，以减少实际试验周期，降低试验耗费，增加测试准确性，提高电力电缆长期使用的安全性.

1 仿真模型与方程

1.1 电力电缆温升等值热路模型

计算电力电缆导体及各护层温度时最重要的部分是暂态计算，在暂态热路中需考虑绝缘层和外护层的热阻以及各层的热容，此外还需要考虑周围介质的热阻和热容.电缆中各层的温度不仅是坐标的函数而且是时间的函数，当高压电力电缆在2U0下进行热循环电压试验时，电缆的介质损耗不能再忽略，在等效热路模型的基础上，不忽略电缆的介质损耗以及金属套损耗时，其在空气中电缆的集中参数等效热路模型如图1所示.

图1 等效热路模型Fig.1 The equivalent thermal circuit model

1.2 温升微分方程

1.2.1 等值热路热流微分方程

由图1所示的热路模型可以得出动态条件下热流微分方程为

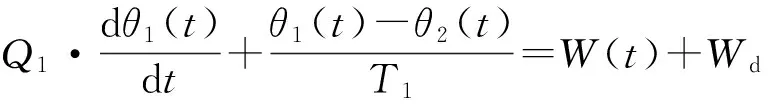
(1)

(2)

(3)

式中：T1为绝缘(含内外屏蔽及阻水层)热阻;T2为外护层热阻;T3为外部热阻;Q1～Q3为电缆各层热容;Wd为介质损耗;W(t)为导体损耗;Ws为金属护层损耗;θ1(t)为导体温度;θ2(t)为金属套温度;θ3(t)为电缆表面温度.

1.2.2 损耗的计算

①导体损耗.在暂态过程中导体损耗是随电阻和电流而变化的时间函数[4].影响导体电阻的因素除了导体自身固有参数以外，其次是导体运行时的温度.计算导体温升时需对导体损耗实时修正，即对导体电阻进行实时修正.在稳态电缆电阻计算的基础之上得到暂态下导体运行时的直流电阻为

R′=R0×[1+α20(θ1(t)-20)].

(4)

式中：R0为20 ℃时导体单位长度的直流电阻，Ω/m，α20为20 ℃时材料恒定质量温度系数.

得到修正之后导体的交流电阻为

R=R0[1+a20(θ1(t)-20)](1+ys+yp).

(5)

式中：yp为邻近因素；ys为集肤效应因素.

修正后导体损耗的计算为

W(t)={R0[1+a20(θ1(t)-20)](1+ys+yp)}·I2.

(6)

②介质损耗.单位长度的绝缘损耗Wd为

Wd=ω·c·U02·tgδ.

(7)

式中：ω= 2πf；U0为对地电压，V；tgδ为在电源系统和工作温度下绝缘损耗因数；c为单位长度电缆电容，F/m.

金属套损耗Ws≈0.

1.2.3 热容的计算

各层热容参数为

Q1=Q0+pQi；

(8)

Q2=(1-p)Qi+p′Qs+Qcp；

(9)

Q3=(1-p′)Qs.

(10)

式中：Q0为导体热容；Qi为绝缘热容；Qs为外护层热容；Qcp为金属护套热容.

式(8)～(10)中p和p′ 为

(11)

(12)

式中：dc为导体外径;Di为绝缘外径;De为电缆外护层外径;Ds为电缆外护层内径.

T1～T3热阻部分的计算参考文献[5-7].

2 电缆热循环试验仿真与效果

根据上文所建立的热路模型及1所列的动态微分方程，基于MATLAB仿真平台结合电缆实际运行环境模拟仿真，并在实际环境中进行试验测试.本次试验所选取的电力电缆型号为YJLW02 290/5 001×2 500单芯电力电缆， 其物理特性参数见表1.

表1 YJLW02 290/500 物理特性参数Tab.1 The physical parameters of YJLW02 290/500

该电缆的绝缘热阻为0.45 K·m/W，外护层热阻T2为0.45 K·m/W，外部热阻为0.13 K·m/W.敷设方式为空气中单根单芯敷设，未受日光照射[8-10]，电缆导体、金属套、表面初始温度为15.6 ℃.试验过程中采用电流互感器实时监控电缆负荷电流，现场如图2所示.

图2 测试现场Fig.2 Test site

2.1 电缆各层的温升特性及介质损耗的影响

电缆施加负荷电流时，电缆各层的温度是随时间变化的时间函数.为了研究给电缆施加恒定电流时电缆各层的温升特性，分析介质损耗对温升特性的影响，试验过程中采用电流加热的方式，从0时给电缆加以2 450 A恒定电流，持续加热30 h.根据热路模型建立的热流微分方程，在MATLAB软件中分别计算出考虑介质损耗和忽略介质损耗时电缆各层理论温升曲线，并与实际测得的温度曲线进行对比分析.所得500 kV电力电缆暂态理论温升曲线图，如图3所示.

图3 电缆各层的温升曲线Fig.3 The temperature rise curves of Cable layers

从图3中可以看出：当电缆通以恒定电流后，电缆各层温度在0～8 h上升最快，上升曲线陡峭，在10 h后趋于稳定，此时影响电缆温度主要是环境温度，随着环境温度的变化电缆各层温度有小幅波动.将图3中忽略介质损耗计算导体温度曲线、考虑介质损耗计算导体温度曲线分别与实测导体温度作差取绝对值，曲线如图4所示.

图4 温差绝对值曲线Fig.4 The absolute value curves of difference in temperature

如图4所示，考虑介质损耗计算导体温度曲线与实测导体温度曲线拟合的更好.考虑介质损耗以后，实测曲线与理论计算曲线存在误差主要因素为：0～8 h电缆周围还未建立稳定温度场，此时影响电缆温升的主要因素是电缆负荷电流，由于实际测试时，施加电流从0 A逐渐升高至2 450 A，并不是严格意义上的阶跃电流，所以在前1 h内实际测得的温升曲线比理论计算温升曲线上升缓慢.10 h以后电缆周围趋于稳定温度场，影响电缆温升的主要因素为环境温度，由于仿真模拟环境温度跟实地试验环境温度不完全一致，因此考虑介质损耗的理论计算曲线与实测温升曲线不能完全拟合，存在小范围温差.

2.2 不同电流负荷时电缆导体温升仿真及效果

为了研究电缆负荷电流超过、低于理论载流量时电缆的温升特性，试验过程中选取3根物理参数相同的YJLW02 290/5 001×2 500单芯电力电缆，在相同实验环境下进行试验.从0时给3根电缆分别施加2 150，2 450，2 750 A恒定电流(2 450 A为该电缆在环境温度为16 ℃下的理论载流量近似值)，持续加热24 h，得到500 kV电力电缆施加不同电流时导体温升曲线图,如图5所示.

图5 电缆导体的温升曲线Fig.5 The temperature rise curves of cable conductor

从由图5中的理论计算曲线和实际测得温升曲线可以看出：通以2 450 A的电缆在加热10 h后温度逐渐趋于电缆长期运行的最高允许温度90 ℃，而通以2 750 A的电缆温度上升快，在加热6 h后就已超过长期安全运行的最高允许温度，并持续上升，在15 h时超过110 ℃，通以2 150 A的电缆导体温度在加热10 h后温度趋于70 ℃.

2.3 电缆热循环试验模拟仿真及效果

目前超高压电缆系统已经构成了许多城市的供电网络骨干，其可靠性直接决定了城市电力传输系统的可靠性[11-13].因此需要在电缆系统进入市场前必须对电缆及其附件系统进行型式试验与预鉴定试验，试验一般按照IEC 62067-3:2006进行，其中热循环载流量试验是尤为重要的试验之一.本次热循环载流量试验中，采用导体电流加热的方式，测试时对电力电缆持续加热8 h，将电缆导体加热至规定温度范围后保持2 h，随后至少自然冷却18 h.试验过程中从0时给电缆施加2 700 A恒定阶跃电流，连续加热8 h后电缆导体温度上升至90 ℃左右，将电流瞬间降至2 400 A，并持续加热2 h，使电缆温度保持在90±2 ℃，10 h后将电流瞬间降至0 A，让电缆自然冷却18 h.根据2.2中所列热流微分方程模型，计算出电缆导体、金属套、表面的温升理论曲线，并与实际试验所测得的数据曲线对比分析，试验结果曲线如图6所示.

图6 热循环试验模拟图Fig.6 Thermal cycling test simulation diagram

从图6可以得知：在0～8 h电缆各层温度变化最快；在8～10 h给电缆施加的电流为2 400 A，电缆导体温度趋于90 ℃，10 h以后，将电流降至为0 A，此时电缆开始缓慢自然冷却，电缆各层温度开始缓慢下降直至24 h逐渐趋于环境温度.

3 结论

(1)通过实测数据对比分析验证了笔者研究的等效热路模型的正确性，为电缆温升试验提供了较为完善的理论模型，为电缆的研发、选型提供了理论依据.通过与实际测试数据对比分析，可减少实验次数，降低耗费.

(2)电缆通以恒定负荷电流后，电缆导体、金属套、表面的温升是一个从暂态逐渐趋于稳态的过程.施加电流0～8 h内电缆周围还未建立稳定温度场，此时影响电缆温升特性的主要因素是负荷电流，电缆各层温度上升较快.在加热10 h后电缆周围温度场趋于稳定，电缆各层温度变化趋于平缓，此时影响电缆温升的主要因素为环境温度.电缆的自然冷却是一个非常缓慢的过程，电缆导体温度自然冷却16 h之后才趋于环境温度.

(3)高压电力电缆热循载流量环试验中，在0～8 h内介质损耗对电缆温升影响不明显，当加热时间超过10 h，电缆周围温度场趋于稳定时由介质损耗造成的误差为3～4 ℃，因此在电缆长期运行时需考虑介质损耗对电缆温升的影响，防止电缆长期处于过热状态加速绝缘老化,影响使用寿命.

[1] 王姗姗，孙华东，易俊，等．电力系统安全稳定相关标准对大电网的适用性综述[J]．电网技术，2013，37(11)：3144-3150．

[2] IEC 62067—3 Calculation of the cyclic and emergency current rating of cables，part 3： Power cables with extruded insulation and their accessories for rated voltages above 150kV(Um=170kV) up to500kV(Um=550kV)Test methods and requirements [S].2006．

[3] 樊友兵，蒙绍新，杨黎明，等．500 kV XLPE电力电缆热循环电压试验导体温度的确定[C]//深圳：中国电机工程学会，2007: 109-112．

[4] 马国栋.电线电缆载流量[M].北京：中国电力出版社，2003．

[5] 刘毅刚，罗俊华．电缆导体温度实时计算的数学方法[J]．高电压技术，2005，3l(5)：52-54．

[6] International Electrotechnical Commission.IEC 60287—1 Calculation of the current rating of electric cables，part 1：current rating equations (100%load factor)and calculation of losses，section l：general[S].Geneva,Switzerland:IEC,2006.1994．

[7] 牛海清，周鑫，王晓兵，等．外皮温度监测的单芯电缆暂态温度计算与试验[J]．高压电技术，2009，35(9)：2138-2143．

[8] 王有元，陈仁刚，陈伟根，等．电缆沟敷设方式下电缆载流量计算及其影响因素分析[J]．电力自动化设备，2010，30(11)：24-29．

[9] 杨永明，陈鹏，陈俊，等．基于耦合场的通风电缆沟敷设电缆载流量计算及其影响因素分析[J]．电力自动化设备，2013，33(7)：139-143．

[10]梁永春，李彦明，柴进爱，等．地下电缆群稳态温度场和载流量计算新方法[J]．电工技术学报，2007，22(8)：185-189．

[11]章健，马旭冰，程晓晓，等．图形化低压电网线损计算与负荷优化配置软件开发[J]．郑州大学学报：工学版，2012，33(3)：44-47．

[12]陆景德，张书鸿，凌惠民，等．排管敷设XLPE电缆稳定载流量试验研究[J]．电力设备，2007，8(9)：1-5．

[13]罗涛，陈民铀，曾灿．电力电缆安全监测中温度场和电场数值关系分析[J]．电力系统保护与控制，2010，38(5)：20-24．

The Research of Power Cable Cyclic Heating Thermodynamic

WANG Guang-bin1, YANG Hai-ma1,2, YANG Hui1,LU Ling3, JIN Zhi-yong3, MA Sheng1, HUANG Ying-ping1

(1.School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology ,Shanghai 200093,China; 2.Shanghai Institute of Technical Physics of the Chinese Academy of Sciences, Shanghai 200083,China; 3.Shanghai LANPO High Voltage Technology & Equipment Co.Ltd. Shanghai 200245,China )

In order to study the temperature characteristics of the voltage power cables current carrying capacity thermal cycling test and influence of ambient temperature and dielectric loss on temperature rise of power cables, in this paper, we improved the cable lumped parameter model equivalent thermal circuit in the air, We established the heat flow equations of the real-time correction for the conductor loss, dielectric loss and the ambient temperature under transient conditions. We simulated the temperature rise of cable conductor and the metal sleeve when applying a constant current to the cable and the influence of dielectric loss on temperature in the working state. We also simulated the transient temperature rise and natural cooling curve of the each layer of in cable thermal cycling current carrying capacity test and fitted with the actual temperature rising curve which had been measured. The results show that: In the high voltage power cables thermal cycling test, the dielectric loss has greater impact on the cable temperature characteristics. We need to correct the conductor loss, dielectric loss and the ambient temperature in real-time.

power cable; dielectric loss; differential equation of heat flow; temperature rise characteristic

2014-08-30；

2014-11-19

国家自然科学基金资助项目(61374197)；上海市闵行区产学研合作计划项目(2013)；上海市教委创新项目(13YZ111)

杨海马(1979-)，男，河北刑台人，上海理工大学讲师，博士，主要从事光电智能仪器、光量子道信和电测试技术等方面的研究，E-mail:snowyhm@sina.com.

1671-6833(2015)01-0105-05

TM247

A

10.3969/j.issn.1671-6833.2015.01.025