基于离散电视频带的频谱接入策略研究

陆彦辉， 张 帅， 穆晓敏， 杨守义

(郑州大学 信息工程学院, 河南 郑州 450001)

基于离散电视频带的频谱接入策略研究

陆彦辉， 张 帅， 穆晓敏， 杨守义

(郑州大学 信息工程学院, 河南 郑州 450001)

基于电视频带的认知网络中主用户为随机出现的无线麦克等设备，其随机行为使得可用频谱离散化，产生许多小于用户需求的频谱碎片.将主用户行为建模为Markov过程，定义频谱占用度、碎片度及统计平均中断概率来分析其行为对系统性能的影响，并提出两种接入策略，策略一加入调整因子并优先选取较少连续信道，策略二基于k-agile接收机，考虑保护带及灵敏度约束，以最小碎片数为目标，非连续地接入频谱，在物理层解决碎片问题，仿真证明二者性能均优于已有策略.

认知无线电；Markov过程；频谱碎片；频谱接入策略；中断概率

0 引言

随着无线技术的发展，频谱紧缺问题俞发严重，而TV频带因其良好的传播特性，且在多数地区存在较大空闲而备受人们关注，由此形成了IEEE 802.22协议[1-3].其中主用户为随机出现的无线麦克等设备，随机占用/释放授权信道，可用频谱被离散为一系列由若干连续信道组成的碎片.而分布式系统没有控制中心，相邻频块间由功率泄露造成的跨频干扰直接影响通信质量，故接入策略应兼顾由碎片导致的可用频谱非连续及跨频干扰问题.

文献[4]基于k-agile接收机解决非连续性问题，但忽略了跨频干扰，文献[5-6]以插入保护频带的方法消除跨频干扰，但未能解决非连续性问题.已有策略未充分考虑非连续及跨频干扰问题，且忽略了频谱结构随主用户的动态变化，使碎片问题的研究缺乏普适性.为此笔者将主用户行为建模为Markov，通过频谱占用度和碎片度分析其对系统性能的影响，并考虑非连续及跨频干扰问题，提出两种接入策略，通过统计平均中断概率衡量策略性能.

笔者通过离散Markov模型，分析主用户行为对频谱结构的影响，并以此提出两种接入策略以解决实际中的频谱碎片问题，提高资源利用率.

1 系统模型

1.1 认知网络模型

基于TV频带的分布式认知网络系统中，次用户通过认知节点AP(Access Point)接入主干网(VHF/UHF频带)，一个AP可连接多个次用户.存在通信需求时由AP选择满足自身及相连次用户需求的可用频段，并将之广播给次用户，次用户随之调整中心频率等参数接入该频段.

而由于主用户的随机行为，主干网中空闲TV频带被离散为一系列碎片，图1为一种具体分布.设信道数为N，这里信道指一个TV信道(6 MHz)，可用信道(未被主用户占用)1、2和3即为一个碎片.由于多个认知网络均可接入主干网，故可用信道上存在来自其它认知网络的传输，即背景传输[6].

图1 频谱结构Fig.1 The structure of spectrum

由此定义空时利用率，即可用信道被其它认知网络占用的比率，其值可由SIFT技术[6]获得，则可用信道共享率为

(1)

(3)

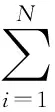
1.2 频谱结构模型

图1只是一种分布情况，而实际频谱结构随主用户行为动态变化，为定性分析，笔者定义频谱占用度ζ和碎片度η

式中：N为总信道数，K为可用信道数，S为碎片数.设信道同构，根据已有研究[2]，设主用户的到达服从泊松分布，到达率为λ，离开服从负指数分布，离开率为μ.将变量K建模为离散Markov，状态空间为{0,1,…,N}，则状态转移概率率为

设稳态概率为TR={T0,T1,…,TN}，由TRR=TR，T0+T1+…+TN=1得:

TR=BA-1.

(4)

其中,R为状态转移矩阵，系数矩阵A，B为：

对于方阵A，若其不满秩，则存在某一行可由其余行表示，假设其中第i行可由其余行表示，则必然存在一组不全为0的{b0,b1,…,bN},使该行各元素均可由其所在列的其它元素表示，即b0·R0,0+b1·R0,1+…+bN·R0,N=0，而由各行元素之和为1，可得b0=b1=…=bN=1，但该组值并不能使行中其它列元素之和为0，即该行不能通过其余行表示，同理方阵A中各行均不可由其余行表示，则假设不成立，方阵A满秩，则由式(4)可得(N+1)列向量TR唯一解.

(5)

由此可通过ξ和η描述主用户行为对频谱结构的影响，二者概率可分别由式(4)和(5)确定.

1.3 问题描述

(6)

2 动态频谱接入策略

2.1 基于连续接入的改进策略

文献[6]策略完全占用可用信道，如信道1共享率为0.6，若共享0.3即可满足需求，则完全占用会造成资源的严重浪费，故策略一加入自适应调整，根据节点实际需求，动态调整占用度，如上述信道1，若共享0.3的信道即可满足需求，则保留该信道上0.3的共享率给下一节点.而为降低实现复杂度，加入调整因子β，依据β逐步调整占用度，释放多余共享率，且优先选择满足需求的最少连续信道.

策略一具体流程如下.

(1)确定总信道数N、节点数L、到达和离开率λ，μ及Bguard，由η和ξ确定信道状态A.

(4)更新信道状态A(Cmin)=0.

time=time+β,ρ(ci)=time,A(ci)=1

M(Cmin)=M(Cmin)-β

end while

2.2 基于非连续的改进策略

如图2所示，连续频谱接入基于1-aigle接收机，只能接入一段连续信道，策略二基于k-agile接收机[4]，在物理层聚合多个非连续信道以解决碎片问题.

但k-agile接收机并非无限制的，其至多能同时接入k个非连续信道，k即为其灵敏度，且接入碎片越多，消耗保护带也越多.故策略二节点以碎片数最小为目标，选择能以最小保护带消耗满足通信需求的频段，可归纳为

(7)

(8)

(9)

其中，kagile为灵敏度，X={xi|i∈{1,2,…,N}.优化问题(7)即为找出一组xi，使其满足约束条件的同时，所消耗的保护带最小.该问题属于整型规划问题，采用遍历搜索法进行求解.

图2 两种接收机比较Fig.2 Comparison of two kinds of receivers

策略二具体流程如下.

(1)确定总信道数N、节点数L、到达和离开率λ，μ及Bguard，由ξ和η确定A.

(3)依次为L个节点选择满足(7)的频段.

forl=1:L

在约束(9)下，根据A搜索所有连续或非连续信道组合，按碎片数由小到大排列，记为MK

fork=1:length(MK)

跳出并记录C，反之Lost(l)=1

endifendfor

更新信道状态A(C)=0

endfor

综上易知，策略一和策略二性能的提升是以复杂度为代价的，策略一根据β调整占用度，调整次数将随β的减少而增大，即与实际需求相差俞小调整次越多.策略二在灵敏度k的限制下，考虑所有可能信道组合，增加了搜索的次数，故两种策略下的复杂度均有所上升.但相较于其性能的提升，付出的复杂度代价是值得的.

3 仿真分析

3.1 保护带大小对系统性能的影响

图3为保护带大小对系统性能的影响.设Bguard为{0.1～1.1MHz}，其它参数不变.由于ξ和η均对结果产生影响，故考虑所有可能的ξ及η，最终结果取均值.

图3 保护带大小对系统性能的影响Fig.3 The impact of guard-band widthon the performance

3.2 频谱占用度对系统性能的影响

图4 ξ对系统性能的影响Fig.4 The impacts of ξ on the system performance

3.3 节点数及灵敏度对系统性能的影响

图5 灵敏度对系统性能的影响Fig.5 The impact the agility on the system

图6 节点数对系统性能的影响Fig.6 The impact of the number of nodes on the system

节点数为1时，由于没有节点再接入，故策略一调整与否对结果无影响.而节点增多时，策略一调整因子优势得以体现，性能优于文献[6].对于策略二，节点数较少时，其灵活性优势更能体现，当节点数较多时，由于总信道数固定，接入的节点越多，其灵活性优势越弱.

4 结论

笔者利用离散Markov，通过频谱占用度及碎片度分析由主用户随机行为产生的碎片问题.并提出两种接入策略，策略一带有调整因子并优先选取较少连续信道，策略二基于k-agile接收机，考虑保护带及灵敏度约束非连续地进行接入.二者虽在复杂上略高于已有策略，但这种代价相较于其性能的提升是值得的.

[1] SHIN K, KIM H, MIN A, et al. Cognitive radio for dynamic spectrum access: from concept to reality [J]. Wireless Communication, IEEE Transactions on Wireless Communications, 2010, 17(6): 66-74.

[2] NAVID T, SONIA A. Modeling and analysis of cognitive radio based IEEE 802.22 wireless regional area networks[J]. IEEE Trans on Wireless Communications, 2013, 12(9): 4363-4375.

[3] KANG K M, JEONG B J. TV band device for TV white space field trial[J]. IEEE ICCE, 2014, 10(1): 450-451.

[4] LILI C, LEI Y, HAITAO Z. The Impact of Frequency-Agility on Dynamic Spectrum Sharing[C]//In Proc of the IEEE DySPAN. Singapore, 2010, 6(4): 1-12.

[5] HOU W, LIN Z, LEI Y, XIUMING S. Guardband Analysis for Distributed OFDMA with User Heterogeneity[J]. Tsinghua Science and Technology, 2011,16(2):83-89.

[6] BAHL P, CHANDRA R, MOSCRIBRODA T, et al. White space networking with Wi-Fi like connec-tivity[C]//In Proc of the SIGCOMM. Spain, 2009:27-38.

[7] BRUALDI R. Introductory Combinatorics[M]. Pearson, 2009: 128-136.

[8] 杨守义，郝万明.认知无线电中考虑公平性的OFDMA资源分配策略[J]. 郑州大学学报: 工学版，2014，35(3)：55-59.

Dynamic Spectrum Access Strategies in the Cognitive Radio Network Based on the Discrete TV Band

LU Yan-hui, ZHANG Shuai, MU Xiao-min, YANG Shou-yi

(School of Information Engineering, Zhengzhou University, Zhengzhou 450001, China)

The unused TV bands are discretized by the behaviors of the random presence of the incumbents, considered as primary users in the cognitive radio network. The spectrum discreteness is ignored by most of the existing strategies, resulting in a mass of spectrum fragments that cannot afford the user’s demand. In the paper, the primary users are modeled as a Markov process, and the spectrum occupancy degree, fragments degree and the statistical average outage probability are defined to analyze the impact of the primary users on system performance. And two strategies are proposed in this paper. The first strategy involves adjustment factor and selects the fewer continuous channels. The second strategy based on the k-agile receiver involves the constraint of agility and guard bands, and selects the minimum non-contiguous fragments to solve the fragments problem in the physical layer. The simulations show that both strategies are superior to the existing strategies.

cognitive radio; Markov process; spectrum fragment; spectrum access strategy; outage probability

2014-08-25；

2014-11-03

国家自然科学基金资助项目(61271421);新世纪优秀人才支持计划资助项目(NCET-12-0699)

陆彦辉(1972-)，女，河南许昌人，郑州大学教授，博士，主要研究方向是无线通信系统资源管理，Email: ieyhlu@zzeu.edu.cn.

1671-6833(2015)01-0092-05

TN943

A

10.3969/j.issn.1671-6833.2015.01.022