CEEMD-FFT在滚动轴承故障诊断中的应用
2015-03-24陆森林
陆森林,王 龙
(江苏大学 汽车与交通工程学院,江苏 镇江 212013)
CEEMD-FFT在滚动轴承故障诊断中的应用
陆森林,王 龙
(江苏大学 汽车与交通工程学院,江苏 镇江 212013)
针对经验模态分解(EMD)在非线性非平稳信号处理中存在模态混叠问题,虽然总体平均经验模态分解(EEMD)能在一定程度上抑制模态混叠问题,但是添加的白噪声不能完全被中和.因此利用补充的总体平均经验模态分解(CEEMD)对降噪监测信号进行分解,减少重构误差,提取最佳的IMF分量,然后对IMF分量进行FFT变换,实现对滚动轴承的故障诊断.通过对实验采集的滚动轴承的振动信号进行分析,证明了该方法的优越性,有一定的使用价值.
滚动轴承;EMD;EEMD;CEEMD分解;故障诊断
0 引言
在当今工业生产规模发展不断要求旋转机械设备日趋大型化、集成化、高速化的背景下,旋转机械设备发生故障,就可能造成重大的经济损失、环境污染、人员伤亡,而滚动轴承恰恰是旋转机械中容易损坏的关键部件.因此,滚动轴承的故障诊断已经变成了一个广泛研究的课题[1].
EMD(Empirical Mode Decomposition)是 Huang 首先提出的一种新型的时频分析方法,能将信号分解为有限个内禀模态函数(Intrinsic Mode Function, IMF), 适合处理非线性、 非平稳信号[2-3].谷泉等[4]对滚动轴承的故障信号进行EMD分解,得到基本模式分量,然后对其做Hilbert-Huang变换求得包络谱,从而提取了滚动轴承的故障信息.但是EMD时频分析方法,最重要的缺点之一是模态混叠的问题[5].Wu等[6]提出的总体平均经验模式分解(Ensemble Empirical Mode Decomposition)方法,能有效解决经验模式分解方法态混叠问题.但是EEMD添加的白噪声不能完全被中和,不具备完备性.姜军生[7]提出的一种迭代的经验模态分解(IEEMD ,Iterative Ensemble Empirical Mode Decomposition),通过添加不同幅度的高斯白噪声去寻找最优高斯白噪声,取得了一定的效果.
因此,补充的总体平均经验模态分解 (Complementary Ensemble Empirical Mode Decomposition,CEEMD)被提出,其主要是通过向待分析信号中添加两个相反的白噪声信号,并分别进行 EMD 分解.CEEMD 在保证分解效果与EEMD相当的情况下,减小了由白噪声引起的重构误差.
本研究采用小波分析对滚动轴承故障信号进行去噪前处理,然后对去噪后的信号进行补充总体平均经验模式分解(CEEMD),对所得到的IMF分量进行快速傅里叶变换(FFT),以达到识别轴承故障的目的,并且通过实验对比,验证了方案的优越性.
1 CEEMD原理
1.1 EMD分解原理
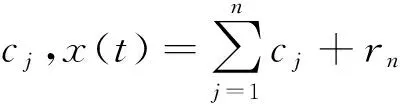
IMF分量所具备的条件:①其极值点和过零点的个数相等或者最多相差一个;②极大值和极小值构成包络线的平均值为零.
图1为经验模态分解的流程图[8],如此重复直到最后一个剩余数据序列rn不可再被分,筛选结束.
1.2 补充总体平均经验模态分解(CEEMD)原理
在EMD方法中,良好的IMF分量的取得与待分解信号的极值点有很大关系.如果信号中极值点时不够多,EMD分解将停止;如果待分解信号极值点分布不够均匀,分解得到的IMF分量将会出现模态混叠的现象.但是,白噪声却可以弥补这一缺点,原因如下:同等幅值随机高斯白噪声,如果进行多次试验,然后把各次实验结果叠加起来,就可以使添加的白噪声相互抵消.利用这一特性,在待分解信号中添加高斯白噪声,可以使信号连续性更好,极值点分布更加合理、均匀,更利于EMD分解的进行,得到最佳的IMF分量,最后通过叠加的方式消除所添加高斯白噪声的干扰.
为了避免上文所述的添加的白噪声不能被完全中和的问题,CEEMD采用的是添加符号相反的随机白噪声,然后进行EMD分解,这样可以减少重构误差,最大限度地中和添加的白噪声,实现对EEMD方法的改进.
具体的操作步骤如下.
(1)在目标数据中加入白噪声序列n1(t);
(2)将加噪数据分解到IMF中,得到第一组内禀模态函数c1j,r1;
(3)在目标数据中加入与第一步符号相反的白噪声序列-n1(t);
(4)将加噪数据分解到IMF中,得到第二组内禀模态函数c-1j,r-1;
(5)在目标数据中加入另一组白噪声序列n2(t),反复运行1,2,3,4,得到,c2j,r2,c-2j,r-2,依次类推,得到n组cnj,rn,c-nj,r-n;
(6)获取分解的IMF的(总体)均值作为最终的IMF结果为:
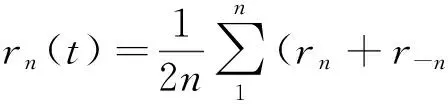
1.3 参数的设置
在CEEMD分解的过程中需要确定两个参数:所添加的高斯白噪声的幅值k和CEEMD 的分解次数n.Wu和Huang建议:k用原信号x(t)的标准偏差乘以一个分数来定义,这样当n为数百次的时候,残留噪声引起的误差一般低于1%.因此,建议当n为100时,k取为原信号标准差的0.01~0.5倍.
2 滚动轴承故障诊断实例
文章所需要的轴承振动实验数据来自Case Western Reserve University 电气工程实验室的滚动轴承故障模拟实验台所测得的数据,实验时电机转速1 797 r/min,负载为0,采样频率为12 kHz速度传感器来拾取.
采用的数据来自电机驱动端型号为6205-2 RS的深沟球轴承,其结构参数如表1所示.
滚动轴承的故障特征频率[9]经计算可得如表2所示.

表1 滚动轴承的结构参数Tab.1 Structure parameters of rolling bearing

表2 滚动轴承的故障特征频率Tab.2 Fault characteristic frequency of rolling bearing Hz
2.1 小波阈值去噪预处理
对于监测得到的振动信号,存在大量的噪声,为了减少模态分解产生的误差,需要对监测得到的振动信号进行初步降噪.为此,笔者选取小波阈值降噪进行预处理.
对于信号x(t),小波阈值去噪步骤如下.
(1)分解.选择合适的小波基并确定分解层次n, 然后对带噪信号x(t)进行n层分解计算,得到一组小波系数wjk.
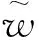
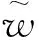
2.1.1 监测信号小波阈值去噪参数的选择
Symlet小波为近似对称的一类紧支正交小波函数,它具有 Daubechies小波系的大部分良好特性,因为它的对称性,故小波系在处理振动信号时,可极大地避免不必要的失真,因此适合对振动信号进行预处理,故轴承信号去噪选择Symlet8小波.
阈值选择Stein无偏似然估计阈值(Rigrsure),并且根据不同层次计算不同的噪声,滚动轴承的振动信号进行4层分解.
相对于硬阈值去噪,软阈值去噪连续性好,去噪信噪比高,均方差小,光滑度较好,故选择软阈值去噪.
2.2 基于CEEMD和FFT轴承故障诊断
本实验的实验数据取自6205-2 RS的深沟球轴承的内圈故障监测信号,图2所示为采集的振动信号的时域频谱及其初步降噪后得到的去噪信号.
图3为内圈故障去噪信号的频域频谱,经过FFT变换所得,由频谱图可知,轴承存在明显的冲击性故障,但是直接进行变换的频谱图无法得知故障特征频率.
为了验证笔者提出的CEEMD方法有效性,对上述去噪信号分别进行EMD,EEMD,CEEMD,分别得到IMF分量,由于篇幅所限,对于各IMF分量就不再一一列出.
其中,在EEMD和CEEMD方法中,所加白噪声的幅值k取值为0.1,分解次数n取100.
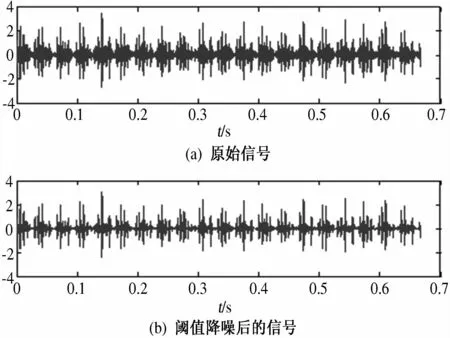
图2 原始信号与初步去噪信号Fig.2 Original signal and de-noising signal
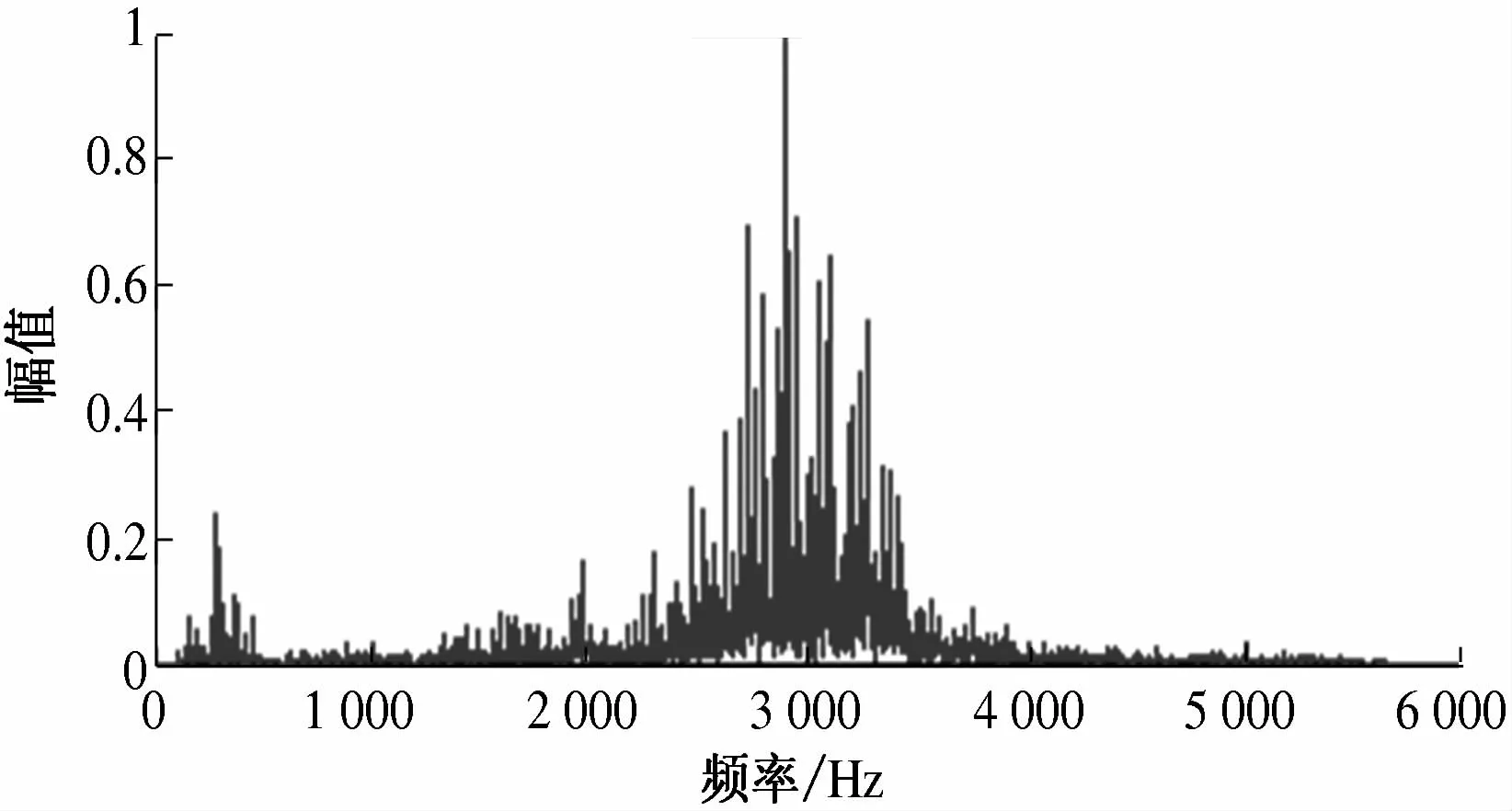
图3 轴承内圈故障信号的FFT频谱Fig.3 Spectrum of bearing with inner fault in FFT
在所得的三组IMF分量中,分别提取第5个分量,进行FFT变换,分别得到频谱图,如图4(a)、4(b)、4(c)所示.
综合对比4(a)、4(b)、4(c),可知通过CEEMD方法得到的第5阶IMF分量,进行FFT之后,得到的频谱图可以清楚辨别出幅值最集中的频率162 Hz,与监测轴承的内圈缺陷旋转特征频率fi相同,其次,振动信号频率次集中的频率为132,192,294,324 Hz,分别为fi-fr,fi+fr,2fi-fr,2fi,其中fr为内圈旋转频率,由此可以鉴别出轴承存在内圈故障.虽然通过EMD,EEMD方法获得频谱图,能在一定的程度上判断出轴承故障,但是CEEMD方法更优越,更有效.
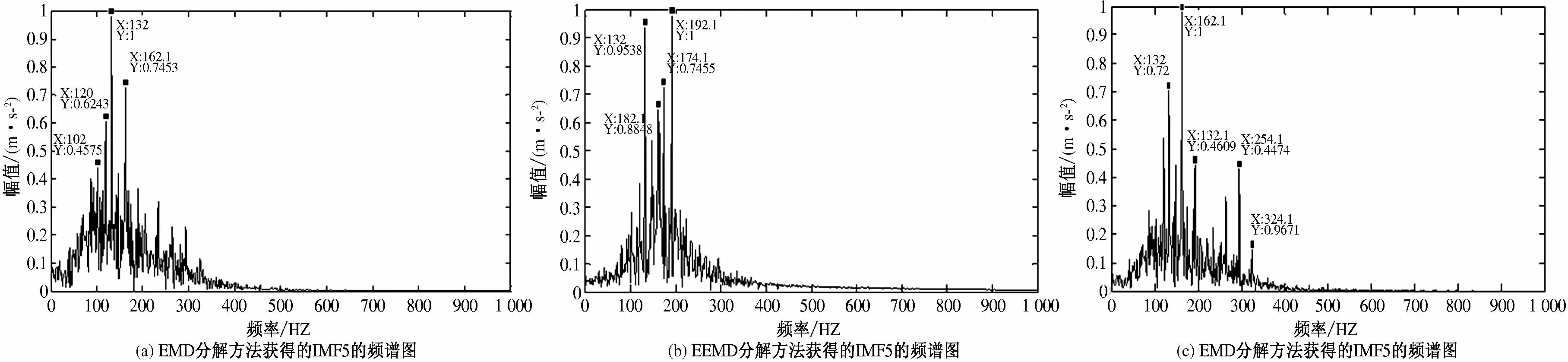
图4 三种分解方法对比Fig.4 Comparison of different decomposition methods in the fermentation
同理,使用外圈故障信号进行测试,用CEEMD方法分解去噪信号,得到频谱图,如图5所示,可以看出频率最集中的地方为102.2 Hz,监测轴承的外圈缺陷旋转特征频率fo基本相同,分别为fo-fr=78 Hz,fo-2f=87 Hz,fo+f=117 Hz,由此可以鉴别出轴承存在外圈故障,从而验证了理论的正确性.
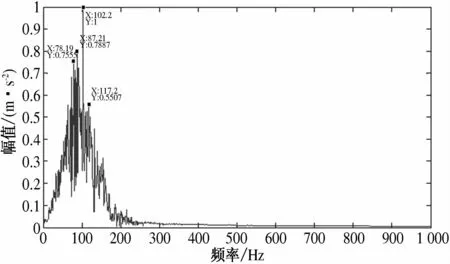
图5 CEEMD分解外圈故障信号获得的IMF6的频谱图Fig.5 Spectrum of IMF6 with CEEMD of outer race fault signal
3 结论
笔者通过EMD和EEMD的改进算法CEEMD,结合阈值降噪和傅里叶变换技术,提取轴承故障特征频率,通过与计算所得的故障特征频率进行对比,实现轴承故障诊断.通过3种方法的对比,CEEMD提高了轴承故障诊断的有效性和准确性,具有一定的实用价值.
[1] 王延博.大型汽轮发电机组轴系不对中振动的研究.动力工程.2004,24(6):768-774.
[2] CHENG J S,YU D J,TANG J S,et al.Local rub-impact fault diagnosis of the rotor systems based on EMD [J].Mechanism and Machine Theory,2009,44:784-791.
[3] YANG B,SUH C S. Interpretation of crack-induced rotor non-linear response using instantaneous frequency [J].Mechanical System and Signal Processing,2004,18 (3):491-51.
[4] 谷泉,陈长征,周昊,等.滚动轴承故障诊断新方法研究[J].机械设计与制造,2013(9):125-127.
[5] WU Z H,HUANG N E.Ensemble empirical mode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.
[6] 雷亚国.基于改进 Hilbert-Huang 变换的机械故障诊断[J].机械工程学报,2011,47(5):71-77.
[7] 姜军生.基于迭代的集总经验模式分解算法的齿轮箱故障特征提取[J] .机械传动,2011,35(12).
[8] 杨宇,于德介,程军圣.基于 EMD 与神经网络的滚动轴承故障诊断方法[J].振动与冲击,2005,24(1):85- 88.
[9] 陈长征,胡立新,周勃等.设备振动分析与故障诊断技术[M].北京:科学出版社.
Application of CEEMD-FFT in Roller Bearing Fault Diagnosis
LU Sen-lin, WANG Long
(College of Automobile and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China)
Modal aliasing problem exists in nonlinear and non-stationary signal processing through Empirical Mode Decomposition (EMD); Ensemble Empirical Mode Decomposition EEMD can suppress modal aliasing problems in some extent, but added white noise can not be completely neutralized. So, complementary Ensemble Empirical Mode Decomposition (CEEMD) is proposed, which can reduce the reconstruction error and extract the best Intrinsic Mode Function (IMF).Then, fast fourier transformation is applied to the IMF component to derive the characteristic frequency of the fault. Analyzing the vibration signal collected by roller bearing experiment proved the superiority of the method and it has some practical value.
roller bearing; EMD; EEMD; CEEMD; fault diagnosis
2014-09-28;
2014-11-13
江苏省自然科学基金项目(06KJD510038)
陆森林(1957-),男,江苏镇江人,江苏大学教授,博士,主要从事振动与噪声与轴承故障诊断的研究,E-mail:305383435@qq.com.
1671-6833(2015)01-0075-04
TH133.3;TP18
A
10.3969/j.issn.1671-6833.2015.01.018
