Hu不变矩在图像识别中的应用与实现

2015-03-23张鸿锋李婉琪曾昭君麦志杰

科技资讯 2014年30期

张鸿锋++李婉琪++曾昭君++麦志杰

摘要：Hu不变矩是图像的一种统计特征，因其具有平移、旋转与比例不变性而被广泛应用于图像识别领域。该文以MATLAB作为技术实现平台，以Hu不变矩作为判断依据，配合数字形态学、欧氏判据等数学方法，通过基于MATLAB的算法进行程序设计，实现区域图像特征数据获取，并与库内图像特征数据进行对比，选出与最接近的一组数据，实现图像识别的目的。计算机模拟结果表明该方法的有效性和可行性。

关键词：Hu不变矩图像特征模式识别应用

中图分类号：TP391 文献标识码：A 文章编号：1672-3791（2014）10（c）-0005-04

模式识别，指使用计算机利用数学技术方法，对表征事物或现象的各种形式的（数值的、文字的和逻辑关系的）信息进行处理和分析，以对事物或现象进行描述、辨认、分类和解释的过程。其中，我们把环境与客体统称为“模式”。该文讨论对数字图像进行模式识别，包含对图像进行特征提取与匹配的过程。

图像特征有两类表示方法，一类是轮廓特征，另一类是区域特征。图像的轮廓特征主要针对物体的外边界，常使用链码，傅里叶描述子、Hough变换进行描述；图像的区域特征则关系到整个形状区域，常用边界特征法、傅里叶形状描述符法、几何参数法、形状不变矩法和小波描述符（Wavelet Deor）等方法描述。而图像特征匹配是指将待检测图像的图像特征与给定图像的数据进行比对，使用如互相关性、欧氏判据等方法，判断两者是否使用同一类型图像的操作。

Hu不变矩作为形状不变矩的其中一种计算方式，具有平移、比例和旋转不变性，这使其在在图像识别的过程中，能减少如待测图像的大小归一化与位置居中等预处理步骤，降低运算成本，提高运算速率。本文将使用Matlab平台，应用Hu不变矩作为特征提取技术，结合数学形态学、欧氏判据等运算方法，实现图像识别功能。

1 Hu不变矩的定义与计算方式

M.K.Hu在1962年提出了Hu不变矩。Hu不变矩是指以图像的低阶（二阶和三阶）归一化中心矩的非线性组合构成的七个量值。Hu不变矩自提出至今，已被广泛应用到图像、字符识别以及工业质量检测等领域。下面叙述Hu不变矩的计算方式。

设二维数字图像用表示，则其阶矩定义为：

（1）

阶中心矩定义为：

（2）

其中。对于二维数字图像，为其质心坐标，表示图像灰度在水平方向上的灰度质心，表示图像灰度在水平方向上的灰度质心。

阶归一化中心矩定义为：

，其中

M.K.Hu将以上代数不变量理论应用于尺度规范化矩，最终构造出下列所示的7个矩不变量，称为Hu不变矩，并验证其对图像的平移、选择和比例具有不变性[1]。以下是7个不变矩的计算公式：

（3）

（4）

（5）

（6）

（7）

（8）

（9）

综上所述，Hu不变矩可以应用以上（3）～（9）所示公式得出结果[2]。

2 统设计与实现

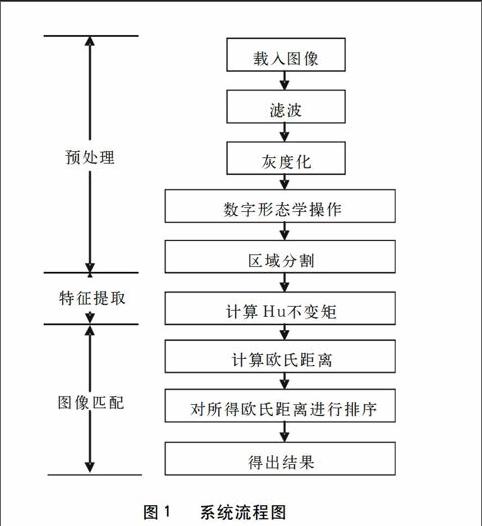
该文应用基于上文公式（3）～（9）编写的Hu不变矩特征提取程序对经过预处理后的图像进行特征提取，使用欧氏判据作为判断依据，将输入图所得矩值与数据库内模板进行比对，实现图像匹配，最后输出判断结果并计数。图1是系统流程图，下面分别叙述系统处理过程。

2.1 预处理

图像分割，是指将图像中相连的区域进行划分并将两个不同区域进行分离。而标记是指把图像矩阵中各个不相连的区域通过赋予不同的数值，便于对各区域进行提取、计数等操作。为实现以上目的，需要使用数学形态学方法对目标图像进行操作。由于该文中使用二值数字形态学，必须对输入的图像进行灰度化处理。已知彩色图片由三个数值矩阵合成所得，则应有彩色图像变换为灰度图像有固定公式如下：

（10）

此后对灰度图像进行灰度二值化处理，为实现自动获取合适的二值化阈值，实现图像背景与目标图像的分离，降低误判率，该文使用调用garythresh函数，应用最大类间方差法进行阈值获取。

对于完成以上预处理操作的图像，开始进行二值数学形态学操作。数学形态学中二值图像的形态变换是一种针对集合的处理过程。其形态算子的实质是表达物体或形状的集合与结构元素间的相互作用，结构元素的形状就决定了这种运算所提取的信号的形状信息。形态学图像处理是在图像中移动一个结构元素，然后将结构元素与下面的二值图像进行交、并等集合运算。例如，如图2所示，假设B（x）代表了结构元素，X代表工作空间，就是用B（x）对E进行腐蚀的结果就是把结构元素B平移后使B包含于X的所有点构成的集合。此时，就是把二值图像各1像素连接成分的边界点去掉从而缩小一层，实现提取骨干信息，去掉毛刺，去掉孤立的0像素的目的，并实现相连区域的分割[3]。该文调用strel函数，用于创建膨胀腐蚀及开闭运算等操作的结构元素对象，且结构元素可根据系统需要修改大小、形状等参数。

在完成了腐蚀后，系统需要对所得图像进行膨胀操作。因为腐蚀操作在运行时，会引起一定的图像边缘信息缺失，为了减少此类信息丢失的影响，系统需要进行膨胀操作。如图3所示，膨胀是数学形态学上面的一个概念，属于腐蚀的逆操作，可认为是把二值图像各1像素连接成分的边界扩大一层，常用于填充边缘或0像素内部的孔。此处应该注意，所用的结构元素必须要与上一步的复式操作相同，使目标图像的信息丢失量降低。

该文先进行了数学形态学的腐蚀操作，而后再进行了数学形态学的膨胀操作，可实现去除图像中孤立点、去除图像毛刺、分割粘连区域的目的。

2.2 特征提取

在上文已经对Hu不变矩的历史与相关公式进行了详细的介绍，此处则不再赘述。本文根据公式（3）～（9）编写不变矩计算程序，并对所得不变矩矩值进行取对数操作。

2.3 特征匹配

该文使用欧氏距离作为判定依据，根据最近邻分类器的方法对待测图像Hu不变矩信息与数据库中Hu不变矩信息进行运算，实现模式识别的功能。以下对欧氏距离与最近邻分类器进行介绍。

欧氏距离（Euclidean distance）也称欧几里得距离，它是一个通常采用的距离定义，它是在m维空间中两个点之间的真实距离。欧氏距离可看作信号的相似程度。

欧氏距离的公式如下所示：

（11）

表示第一个点的第维坐标，表示第二个点的第维坐标；

维欧氏空间是一个点集，它的每个点可以表示，其中是实数，称为的第个坐标，两个点和之间的距离定义为上面的公式。

通过计算各个图像不变矩与给定图像模板的不变矩之间的欧式距离，可以判断图像与各个模板间的相似程度。对输入的数字图像与给定的数字图像模板进行对比，可实现自动分辨输入图像是否输入给定模板的同类图像，并选出其最可能的形状类型。

根据以上的计算公式与判断依据，编写了本系统的模式识别操作模块。通过循环结构，使输入数据与数据库里的数据进行比对，实现模块功能，并实现计数功能。