航姿参考系中磁传感器误差补偿的研究

高延滨，胡守雷，何昆鹏，刘辉煜

(哈尔滨工程大学自动化学院，黑龙江哈尔滨150001)

低成本的航姿参考系统越来越广泛的用于无人机和矿藏探测、钻井等领域中，地磁传感器作为其中一部分通过测量地球磁场为载体提供航向角。地磁磁场是地球的天然物理场，连续分布且非常稳定，可作为理想的参考基准［1］，可以采用三轴地磁传感器测量载体的总磁场，两轴加速度计测量载体的姿态角，通过误差补偿算法获得载体的航向角。由于地磁场的频谱范围很宽，地磁场探测很容易受到载体本身及其电子仪器等产生的地磁干扰［2］，这些干扰会引起地磁场的畸变，这些干扰可等效于地磁传感器三轴磁场数据的零位误差、标度因数和非正交误差，并可由Possion数学模型来描述［3］。目前，针对全姿态下的三轴地磁传感器补偿算法有最小二乘递推法［4］、神经网络法［5］、十二位置翻转法［6］、椭圆假设法［7］、椭球假设法［8］。前3种补偿方法都需要外部航向参考作为基准，对外部设备要求较高;椭圆假设法只需在水平面上旋转一圈便能拟合出椭圆参数，在无外部航向基准时便能完成自动校正，但要求载体只能在水平面上运动，不适用于有水平倾角的情况;椭球假设拟合出来的椭球模型只有9个参数，文献［8］阐述了用不同方法拟合椭球参数所得的精度，文献［9］利用最大似然估计进行误差参数拟合，文献［10］提出了一种基于递归的椭球拟合算法，能根据从地磁传感器采集到的数据自适应的更新校准参数。目前国内对椭球拟合方法的研究较为深入，但对标定数据的空间分布对椭球的拟合精度和误差补偿效果的影响研究很少，文献［11］指出标定位置的分布对补偿参数有很大影响，并提出等面积均匀取点原则;文献［8］分析了当选取的数据在几何位置过于接近时，使算法难以收敛，并提出了采用最值法使数据尽量均匀分布在椭球曲面上，减少误差;文献［12］提出了等夹角均匀取点算法，并通过仿真实验验证等夹角均匀取点优于等面积均匀取点;3种数据选取算法都具有一定的局限性，最值法无法准确判断数据分布是否合理，后2种算法需要依靠外部设备。

本文利用基于模糊逻辑系统的算法，根据设定和标定数据空间分布相关的指标，通过模糊逻辑推理，得到椭球拟合误差，根据误差大小自动判断数据空间分布是否合理。

1 三轴地磁传感器误差模型分析

综合地磁传感器受环境干扰和制造工艺的影响，在任意姿态下，三轴地磁传感器的实际测量输出Hb=［HbxHbyHbz］与理想的地磁场向量Hn=［HnxHnyHnz］之间的关系如下:

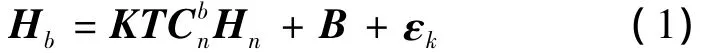
式中:K在理想的情况下为一个三阶单位矩阵，由于软磁材料的干扰，K的主对角线接近1，其他元素接近于零的畸变矩阵;T为安装误差和地磁传感器3个敏感轴不正交误差;B=［BxByBz］为硬磁材料引起的零点误差;是从东北天坐标系到载体坐标系的状态转移矩阵;εk为传感器测量噪声。测量噪声εk可以通过多次测量进行消除，由式(1)可得地磁场矢量Hn为

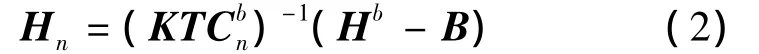
地磁场标量值||Hn||在一定的小范围内可看作是一个定值，令M=(KTC)－1，则式(2)可写为Hn=M(Hb－B)，则

式中:MTM只需为严格对角占优矩阵便是正定阵，而通常软磁干扰中的轴间干扰非常小，可以保证MTM为严格对角占优［12］，则式(3)表示一个椭球面。则将式(3)写成一般表达式:

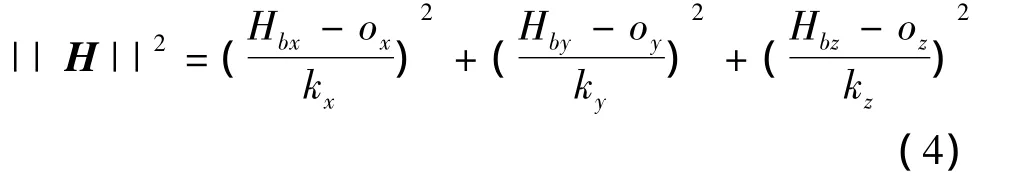
式中:||H||为地球地磁场大小，是一个常量。均方差函数为

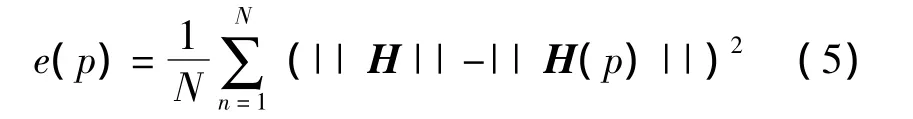
式中:N为标定数据样本的大小，通常求取均方差(MSE)函数最小值来拟合参数p=(kx，ky，kz，ox，oy，oz)。

2 标定位置分布合理性判定指标选择

在理想的磁场环境下，在同一地点三轴地磁传感器输出位于一个以原点为中心，当地磁场强度为半径的一个球面上，但由于存在各种干扰和误差，输出发生畸变，球面模型变形成一个椭球面，通过最小二乘法拟合出椭球面参数，再把椭球面逆变成球面，逆变的校准矩阵由拟合参数p给出，通过仿真实验证明，标定位置在椭球面上的分布会影响椭球拟合的精度［12］。本文通过模糊逻辑系统判断标定数据的合理性，需要选择能够反映数据空间分布信息的判定指标，选择如下3个判定指标:

1)在文献［13］中将样本数据转化为在球坐标系(r(k)，φ(k)，θ(k))上表示，k=1，2，…，N。通过把数据投影到二维坐标系，每个数据点用坐标(φ(k)，θ(k))来表示，其中 －90°≤θ＜90°，－180°≤φ＜180°。如图1所示，得到数据的分布情况，将(φ(k)，θ(k))分成许多小的区间，如果数据分布越合理，那么没有数据分布的区间数就会很少，对没有数据分布的区间进行统计，将判定指标X定义为

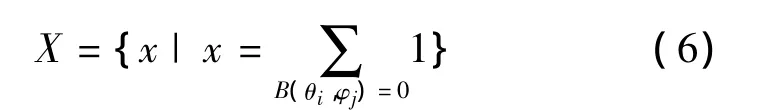
式中:B(θi，φi)表示样本数据投影在区间(φi≤φ ＜φi+1，θj≤θ＜θj+1)内的数据个数。

图1 地磁测量数据的二维分布统计Fig.1 Measurements of magnetic field in 2D projection

2)判定指标Y定义为样本数据点在3个坐标轴上的最长距离之和，如图2所示，表达式如下:

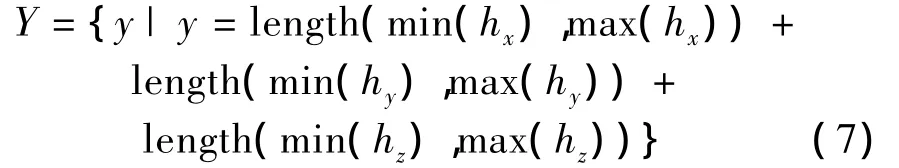
式中:hx、hy、hz分别为样本数据在x、y、z 3个坐标轴上的集合。

3)一个样本数据点所组成的凸包的最小体积也能反映数据的分布，将指标Z定义如下:

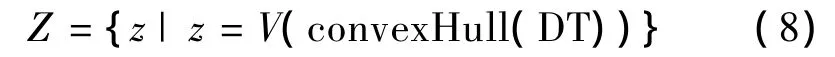
其中，convexHull为数据点组成的凸包体，DT为样本数据的点集，如图3所示。

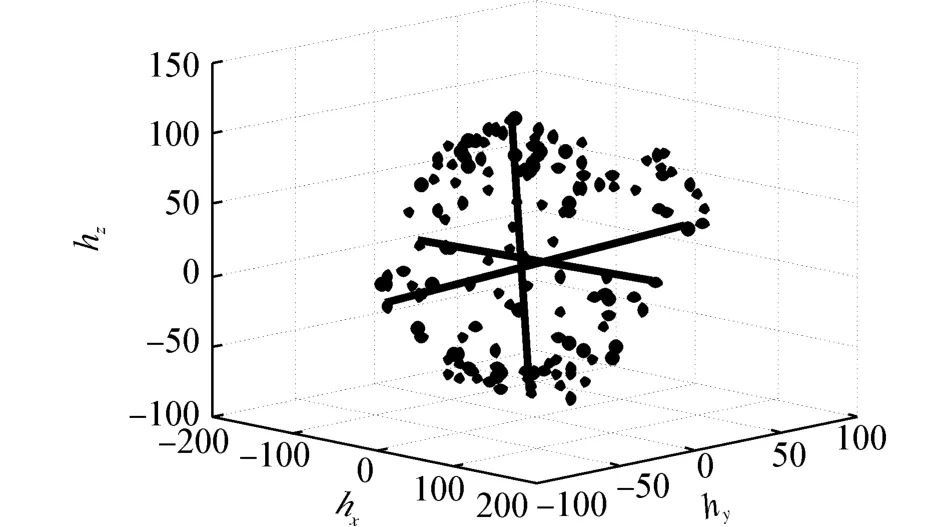
图2 三维数据的最长距离选取Fig.2 Choice of the longest distance of 3D data

图3 地磁数据组成的最小体积的凸包Fig.3 The convex hull composed of geomagnetic data

3 模糊逻辑推理

定义模糊输入变量X、Y、Z和输出变量e(p)的模糊集为S(small，小)，M(middle，中)，L (large，大)，所选择的3个指标和椭圆拟合误差之间没有确定的误差函数关系，这可能导致2组完全分布不同的数据，有着相近的校准误差，但是可以认为拟合误差和3个判定指标之间存在一种模糊关系，根据所选指标的含义可知各个指标与校准误差之间的关系如下:

1)若采样数据在φ-θ平面内的分布面越广泛，即X的取值越小，表明球面上采样数据越均匀，则校准误差越小，反之越大;

2)若采样数据在3个坐标轴上的距离之和越大，即Y越大，表明采样数据的跨度比较大，则校准误差越小，反之越大;

3)若采样数据所组成凸包的最小体积越大，即Z越大，表明采样数据包含的空间越大，则校准误差越小，反之越大。

根据上述关系设计Takagi-Sugeno-Kang(TSK)模糊逻辑系统，定义27条模糊推理规则，列举其中9条规则如下:

1)if X=S and Y=S and Z=S then e(p)is L;

2)if X=S and Y=M and Z=M then e(p)is M;

3)if X=S and Y=L and Z=L then e(p)is S;

4)if X=M and Y=S and Z=S then e(p)is L;

5)if X=M and Y=S and Z=L then e(p)is M;

6)if X=M and Y=L and Z=L then e(p)is S;

7)if X=L and Y=S and Z=S then e(p)is L;

8)if X=L and Y=M and Z=M then e(p)is M;

9)if X=L and Y=L and Z=L then e(p)is S。

在算法中采用解中心去模糊化方法解算椭球参数拟合误差。

4 实验分析

为了对所提模糊逻辑算法的可行性进行验证，设计仿真实验，实验步骤如下:

1)旋转地磁传感器采集3 000个样本点，将其按顺序分15组，每组200个数据，每组数据的分布区间如图4所示，其中细黑线表示200个采样数据的分布区间，粗黑线表示采样数据按升序排列后第51个到第150个数据的分布空间，圆圈表示第101个数据所在的位置。从图4中可以看出第1组数据在x、z方向的分布区间较小，以及第9组数据在x、y方向的分布区间较小外，其他数据的分布区间较大。

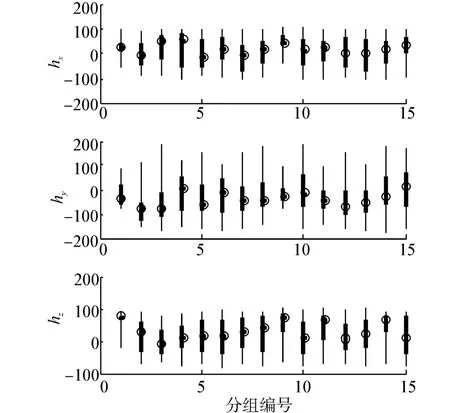
图4 地磁数据的分布Fig.4 The distribution of geomagnetic data

2)依次选取每组数据用最小二乘法进行椭球参数拟合，并用拟合所得参数对所采集的3 000个样本点计算其均方误差，作为实际误差。

3)依次计算每组数据的3个分布指标，并对其进行归一化处理:

Xnorm=X/648，(φ-θ平面每10°划分一个区间);

Ynorm=Y/555，(根据经验，所拟合的椭球的3个轴向最大距离之和大约为555);

4)以3个指标为输入变量，采用模糊逻辑系统求出该组数据的拟合误差，并与步骤2)所计算出的实际误差进行对比。

5)对实际误差与模糊逻辑系统计算出的误差进行标记，当均方误差小于0.02时即认为数据采样合理，“1”表示数据采样合理，“0”表示数据采样不合理。

仿真结果如图5所示，从图5中可以看出模糊逻辑系统的输出与实际误差比较吻合，除第1组和第9组数据误差较大，采样不合理外，其余数据误差均较小，采样比较合理，和图4数据统计结果一致，第1组和第9组数据分布不合理，其他13组数据的分布都满足要求。

图5 实际误差与模糊逻辑输出对比Fig.5 The actual error comparison with fuzzy logic output

5 结束语

本文针对校正数据分布不合理导致地磁传感器在线标定精度不高的问题，提出了基于模糊逻辑系统的数据合理性判定方法，通过对标定数据的3个分布特性指标的计算，进行模糊逻辑推理得到拟合误差。通过实验分析可知，该方法能很好的通过数据分布得出采样数据的合理性，从而为是否对该组数据进行最小二乘拟合提供了依据。

所提出的方法只能对采样数据的合理性进行分析，如何通过对已有数据进行分析从而指导下次数据如何采样，以及如何剔除各组采样数据中偏差较大的数据，还有待于进一步研究。

［1］刘建敬，张合，丁立波，等.地磁信息感应装定系统及其插值算法［J］.中国惯性技术学报，2011，19(6):692-695.

LIU Jianjing，ZHANG He，DING Libo，et al.Geomagnetic information induction setting system and interpolation algorithm［J］.Journal of Chinese Inertial Technology，2011，19 (6):692-695.

［2］黄学功，王炅.地磁信号检测系统误差分析与补偿方法研究［J］.兵工学报，2011，32(1):33-36.

HUANG Xuegong，WANG Jiong.Error analysis and compensation methods for geomagnetic signal detection system［J］.Acta Armamentarii，2011，32(1):33-36.

［3］LI Zhi，LI Xiang，WANG Yongjun.A calibration method for magnetic sensors and accelerometer in tilt-compensated digital compass［C］//Proceedings of 9th International Conference on Electronic Measurement and Instruments.Guilin，China:2009:868-871.

［4］郭鹏飞，华春红，任章，等.基于递推最小二乘的航姿系统罗差校正［J］.中国惯性技术学报，2008，16(1):24-27.

GUO Pengfei，HUA Chunhong，REN Zhang，et al.Magnetic deviation compensation using recursive least square for AHRS［J］.Journal of Chinese Inertial Technology，2008，16(1):24-27.

［5］马斌良，黄玉美，史恩秀，等.基于神经网络代数算法的电子罗盘的标定［J］.仪器仪表学报，2008，29(11): 2304-2309.

MA Binliang，HUANG Yumei，SHI Enxiu，et al.Calibration of electronic compass based on neural network algebra algorithm［J］.Chinese Journal of Scientific Instrument，2008，29(11):2304-2309.

［6］张娇，陈静，杨栓虎，等.三轴磁阻式传感器标定方法研究［J］.弹箭与制导学报，2010，30(6):46-48.

ZHANG Jiao，CHEN Jing，YANG Shuanhu，et al.The study of calibration method of magnetic resistance sensor［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2010，30(6):46-48.

［7］秦勇，赵杰，王晓宇.基于椭圆拟合误差补偿算法的数字磁罗盘［J］.吉林大学学报:工学版，2009，39(2):489-493.

QIN You，ZHAO Jie，WANG Xiaoyu.Digital magnetic compass based on ellipse matching error compensation algorithm［J］.Journal of Jilin University:Engineering and Technology Edition，2009，39(2):489-493.

［8］朱建良，王兴全，吴盘龙，等.基于椭球曲面拟合的三维磁罗盘误差补偿算法［J］.中国惯性技术学报，2012，20 (5):562-566.

ZHU Jianliang，WANG Xingquan，WU Panlong，et al.Three-dimensional magnetic compass error compensation algorithm based on ellipsoid surface fitting［J］.Journal of Chinese Inertial Technology，2012，20(5):562-566.

［9］VASCONCELOS J F，ELKAIM G，SILVESTRE C，et al.Geometric approach to strapdown magnetometer calibration in sensor frame［J］.IEEE Transactions on Aerospace and E-lectronic System，2011，47(2):1293-1306.

［10］PYLVANAINEN T.Automatic and adaptive calibration of 3D field sensors［J］.Applied Mathematical Modelling，2008，32(4):575-587.

［11］MERAYO J M G，BRAUER P，PRIMDAHL F，et al.Scalar calibration of vector magnetometers［J］.Measurement Science and Technology，2000，11(2):120-132.

［12］刘艳霞，李希胜，冯毅博，等.三轴磁罗盘标定位置分布的研究［J］.仪器仪表学报，2013，34(3):684-690.

LIU Yanxia，LI Xisheng，FENG Yibo，et al.Research on calibration position distribution of three-axis magnetic compass［J］.Chinese Journal of Scientific Instrument，2013，34(3):684-690.

［13］CAMPS F，HARASSE S，MONIN A.Numerical calibration for 3-axis accelerometers and magnetometers［C］// Proceedings of the IEEE International Conference on Electro/Information Technology.Windsor，Canada:2009: 217-221.