放宽静稳定性高超声速飞行器的增稳控制方法

梁冰冰，江驹，吴雨珊，甄子洋

(1.南京航空航天大学自动化学院，江苏南京210016;2.空间物理重点实验室，北京100076)

当前高超声速飞行器受到军事发达国家的重点关注。当飞行器从亚声速向超声速飞行过渡时，由于气动焦点大幅度后移，会产生很大的稳定裕度，导致操纵效率降低。为了使高超声速飞行器在整个飞行包络中都具有良好的稳定性和操纵性，通过放宽静稳定性将在亚声速飞行状态下的飞行器设计为静不稳定，这样当超声速飞行时会具有比普通飞机小的正稳定裕度，而亚声速时的静不稳定飞行器则需要通过增稳控制系统保证其稳定性和操纵性。

针对增稳系统设计，经典反馈增稳控制通常包括俯仰角速度反馈、迎角反馈和法向过载反馈。冯小刚等采用迎角和俯仰角速度组合反馈增稳方案对民机进行了增稳仿真［1］。陈创将俯仰角速度和法向过载反馈到升降舵通道实现大型客机增稳系统设计［2］。然而经典反馈增稳控制难以有效处理高控制精度要求的多输入多输出系统，最优控制逐步发展并应用于放宽静稳定飞机增稳系统的设计过程中。王一超等采用LQR方法实现了对放宽静稳定性客机的增稳控制［3］。丁立东研究了LQ最优控制在民机飞行控制系统的应用［5］。

然而，关于高超声速飞行器的增稳控制研究的文献成果报道甚少。本文以某高超声速飞行器为研究对象，气动导数采用放宽静稳定性后的拟合值，利用经典反馈增稳控制方法和LQ最优控制方法设计纵向增稳系统，并作了仿真对比验证。

1 问题描述

飞行器纵向静稳定性用纵向静稳定度Sm来度量，定义为给定马赫数Ma条件下，飞行器全机焦点与重心在平均气动弦长的相对位置差，表示为

当Sm＞0时，飞行器为静稳定;Sm=0时，飞行器为中立稳定;Sm＜0时，飞行器为静不稳定。随着飞行马赫数增加，飞行器从亚声速飞行跨越到超声速甚至高超声速飞行，由于焦点大幅度后移，稳定度Sm可能增大3～4倍。图1为本文研究的某高超声速飞行器稳定度拟合曲线。从图1可以看出，当迎角位于配平迎角 α=3°时，亚声速飞行(Ma=0.3)Sm≈ 0.35，而高超声速飞行时(Ma=5)Sm≈0.6，稳定度数值增加约2倍。

图1 某高速声速飞行器稳定度拟合曲线Fig.1 Stability fitting curve of the hypersonic vehicle

稳定度的增加会产生很大的稳定裕度，使得操纵费力，飞行器机动能力变差;同时也会形成很大的俯仰力矩，这样就要求平尾提供更大的正俯仰力矩来配平，因而导致平尾面积需要增加;另一方面，机翼升力除了要与飞机重量相平衡外，还要平衡尾翼的负向升力，因而使得总升力减少。由于以上提到的静稳定度过大给飞行器带来的危害，要对高超声速飞行器进行放宽静稳定度设计，在亚声速飞行时，将飞行器设计为静不稳定，考虑到静不稳定给飞行员的操纵带来很大困难，因此必须通过增稳或控制增稳系统进行控制，以保证飞机在整个飞行包线内是稳定的。为此，增稳控制系统的设计对于放宽静稳定的高速声速飞行器极为重要。

2 高超声速飞行器数学建模

2.1 非线性数学模型

某高超声速飞行器的控制输入为发动机节流阀调定值βc和升降舵偏转δe，输出为飞行器短周期运动模态下2个主要参数:迎角α和俯仰角速率q。

某高超声速飞行器在亚声速飞行条件下的运动模型方程为［6-7］

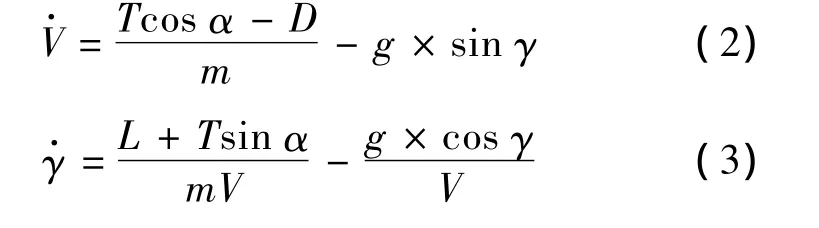
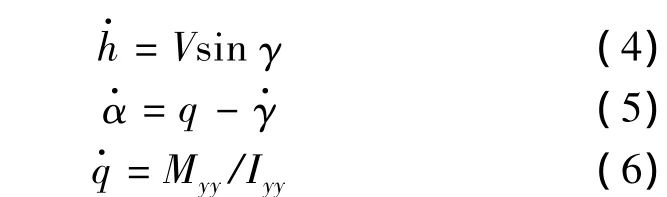
式中:

其中，CL、CD、CM(α)和CM(q)由已知气动参数插值拟合得到，CM(δe)=ce(δe－α)，CT为推力系数，且

假设在亚声速飞行状态下，高超声速飞行器的质量m、俯仰力矩惯性积Iyy、飞机表面积s、翼弦长c存在摄动，即表示为

2.2 线性化数学模型

由于经典反馈控制的控制增益是基于系统传递函数设计的，而最优控制方法需要利用非线性系统的线性模型来设计增稳控制律，因此，需要对亚声速飞行条件下的高超声速飞行器非线性模型作线性化处理。

高超声速飞行器的气动参数CL、CD和CM根据部分已知的放宽静稳定气动参数插值拟合得到，图2给出Ma=0.8气动系数插值拟合曲线。

使用Matlab/Trim工具得到放宽静稳定高超声速飞行器在亚声速飞行的一个配平点为:v= 167.01 m/s，α=2.89°，q=0(°)/s，δe=1.74°，δt=0.34，h=4 544.86 m，得到飞行器在配平点处舵偏为正，由于放宽静稳定性的高超声速飞行器只有当舵偏为正产生向上升力时才能保持力与力矩平衡，因此可以验证本文所使用的气动参数插值拟合数据符合要求。

图2 Ma=0.8时气动系数的插值拟合曲线Fig.2 Fitting curve of aerodynamic coefficient at Ma=0.8

使用Matlab/Linmod工具利用小扰动原理对其在配平点处线性化，并将纵向与横侧向解耦，得到纵向短周期模态的状态空间模型为

3 增稳系统设计

3.1 基于经典反馈控制的增稳系统设计

将高超声速飞行器的非线性模型处理成多个单输入单输出线性时不变系统，即可利用根轨迹法为闭环增稳系统选择合适的系统增益，以改善闭环系统的动态性能，获得满意的自然频率和阻尼比。

纵向运动的初始阶段，短周期运动占主导地位，其过渡过程时间很短，可以忽略长周期运动。纵向增稳的目的就是为飞机的短周期模态提供满意的自然频率和阻尼比，从而改善飞机的阻尼特性和稳定性。基于经典反馈控制的纵向增稳控制一般采用俯仰角速率信号反馈、迎角信号反馈、法向过载信号反馈以及多种信号组合的综合反馈结构。不同反馈结构的优缺点总结见表1［8］。

表1 不同反馈结构的增稳控制性能比较Table 1 Comparison between augmentation control methods

基于上述比较，本文采用迎角和俯仰角速度组合反馈增稳方案，这种增稳方案也是现代飞机电传操纵系统常用的一种方案，它既保证了控制精度，又提高了可靠性。为此，增稳控制系统的反馈控制律设计为

不考虑舵回路的动态特性，得到俯仰角速率和迎角反馈的增稳控制结构如图3所示。

图3 基于俯仰角速率和迎角反馈的增稳控制结构Fig.3 Augmentation control method diagram based on pitch angle rate and angle of attack

因此，利用根轨迹方法调节kα、kq值，可使纵向短周期模态达到理想的频率和阻尼比，最终选取kα=3，kq=10。

接下来进行仿真验证，仿真初始条件为高超声速飞行器在亚声速飞行阶段的一个配平点为:v= 167.01 m/s，α=2.89°，q=0(°)/s，δe=1.74°，δt=0.34，h=4 544.86 m，将设计的增稳控制系统代入第2节所描述的非线性模型中，用以验证增稳控制系统的有效性。

数值仿真中，在非线性模型描述的高速声速飞行器中，加入迎角和俯仰角速度组合反馈增稳系统，得到高速声速飞行器迎角、俯仰角速率响应曲线如图4所示。可以看出，放宽静稳定性后的飞机迎角响应曲线和俯仰角速率响应曲线在短周期内振荡明显，超调较大，动态性能较差。设计增稳系统后的飞机迎角和俯仰角速率均在1 s内达到稳态，动态过程迅速无振荡，仿真曲线超调较小，基本无静差，达到了理想的增稳效果。

图4 采用经典反馈控制系统的响应曲线Fig.4 Response curve of classical feedback control system

3.2 基于LQ最优控制的增稳系统设计

相比经典控制理论而言，LQ最优控制能有效处理高控制精度要求的多输入多输出系统。基于高速声速飞行器的状态空间线性方程，设计状态反馈增稳控制律为

式中:G为反馈系数矩阵。最优控制的性能指标函数表示为

式中:K(t)通过求解如下黎卡提矩阵微分方程得到

然而上述微分方程很难得到解析解，故可写成差分方程形式，从而得到数值解。

数值仿真中，通过选取适当的Q、R矩阵得到最优控制律，在非线性模型描述的高速声速飞行器中加入LQ最优增稳控制系统，得到高速声速飞行器迎角、俯仰角速率响应曲线如图5，可以看出，飞机迎角和俯仰角速率均在1 s内达到稳态，动态过程迅速且无振荡，仿真曲线几乎无超调，基本无静差，达到比经典反馈控制更理想的增稳控制效果。

图5 采用LQ最优控制系统的响应曲线Fig.5 Response curve of LQ optimal control system

3.3 模型参数不确定性下2种增稳控制系统鲁棒性比较

从上述仿真中已经得出，LQ最优增稳控制系统比经典反馈增稳控制系统超调更小，响应时间更快，达到更佳的增稳效果。然而，高超声速飞行器的参数不确定性较普通亚声速飞行器更加显著，因此下面对2种不同增稳控制系统的鲁棒性进行仿真对比研究。

仿真研究2种方法下飞行器模型参数未摄动、摄动+20%和摄动－20%时的增稳控制效果。图6给出了经典反馈控制下参数未摄动、摄动+20%和摄动－20%的迎角和俯仰角速率输出响应，图7为LQ最优增稳控制下参数未摄动、摄动+20%和摄动－20%的迎角和俯仰角速率输出响应。

由仿真结果可以看出，当飞行器参数摄动时，经典反馈控制会使迎角和俯仰角速率产生 ±0.01rad/ ±0.01 rad/s波动，而LQ最优控制仅会使迎角和俯仰角速率产生 ±0.001 rad/±0.001rad/s波动，因此采用LQ最优控制设计的增稳系统拥有更好的增稳效果和更理想的抗鲁棒特性。

图6 参数摄动下采用经典反馈系统的响应曲线Fig.6 Classical feedback control responses with parameter perturbation

图7 参数摄动下采用LQ最优控制系统的响应曲线Fig.7 VLQ optimal control responses with parameter perturbation

4 结束语

通过研究发现，LQ最优增稳控制系统比目前应用较多的经典反馈控制系统具有更好的动态增稳效果和抗模型参数不确定的鲁棒特性，更加适用于非线性特性强烈、对外界环境变化敏感的高超声速飞行器。

［1］冯小刚，李俨，崔永青.民机放宽静稳定性的研究［J］.电子设计工程，2013，21(19):118-119，122.

FENG Xiaogang，LI Yan，CUI Yongqing.Research on relaxed static stability of civil aircraft［J］.Electronic Design Engineering，2013，21(19):118-119，122.

［2］陈创.主动控制技术在大型民用飞机上的应用研究［D］.上海:上海交通大学，2013.

CHEN Chuang.Research on large civil aircraft based on active control technology［D］.Shanghai:Shanghai Jiao Tong University，2013.

［3］王一超，江驹，王新华，等.放宽静稳定性大型客机的LQR控制律设计［J］.飞行力学，2012，30(6):519-522.

WANG Yichao，JIANG Ju，WANG Xinhua，et al.LQR in control law design for a relaxed static stability large civil aircraft［J］.Flight Dynamics，2012，30(6):519-522.

［4］丁立冬.飞翼式无人机纵向增稳主动控制技术研究［D］.南京:南京航空航天大学，2007:20-34.

DING Lidong.Research on longitudinal stability augmentation system using active control technique for flying wing unmanned combat aerial vehicle［D］.Nanjing:Nanjing University of Aeronautics and Astronautics，2007:20-34.

［5］WANG Q，STENGLE R F.Robust nonlinear control of a hypersonic aircraft［C］//AIAA Guidance，Navigation and Control Conference.Reston，USA:AIAA，1999:413-423.

［6］MARRISON C I，STENGEL R F.Design of robust control systems for a hypersonic aircraft［J］.Journal of Guidance，Control，and Dynamics，1998，21(1):58-63.

［7］徐奎.民用飞机纵向增稳系统分析及最优控制器设计［J］.航空科学技术，2013(1):31-33.

XU Kui.Analysis and design of a longitudinal stability augmentation control system for a civil aircraft［J］.Journal of Aeronautical Science and Technology，2013(1):31-33.