第一性原理研究GaP的电子结构、光学性质及各向异性

刘 丽， 韦建军, 吐尔迪·吾买尔， 冯 艳, 彭 敏

(1. 新疆工程学院, 乌鲁木齐 830000; 2. 四川大学原子与分子物理研究所, 成都 610065)

第一性原理研究GaP的电子结构、光学性质及各向异性

刘 丽1,2， 韦建军2, 吐尔迪·吾买尔1， 冯 艳1, 彭 敏1

(1. 新疆工程学院, 乌鲁木齐 830000; 2. 四川大学原子与分子物理研究所, 成都 610065)

利用基于密度泛函理论(DFT),采用赝势平面波方法和广义梯度近似法(GGA)研究了闪锌矿ZB结构和盐岩RS结构GaP的基态电子结构、光学性质，根据能带理论初步研究GaP基态能带结构、总态密度(DOS)和分波态密度(PDOS),并计算出吸收系数，反射率，复介电函数，复折射率及能量损失函数.还计算了闪锌矿结构的GaP的各向异性.

GaP； 电子结构； 光学性质； 第一性原理

1 引 言

III-V族化合物半导体材料在众多领域里有着不可代替的位置，包括高速逻辑电路，光电器件，微波器件和太阳能电池能，其中GaP半导体具有高杨氏模量，低吸收系数，低内应力，以及宽波段红外透明，其发光范围涵盖红色至黄绿色范围，是LED主要使用材料之一，与砷化稼材料一起打开了光电器件的市场.常见的GaP材料有NaCl结构和ZnS结构等，不同的结构对其光学性能的影响较大，早在上世纪八十年代就掀起了对GaP研究的热潮，jakste[1]等人用从头算的方法研究了声子的态密度，估算了电子光子的散射时间，通过谷内声子更加深刻地认识到电子的去激发.Rashid等[2]通过密度泛函理论研究了GaP的结构及电学性质，比较了其体弹模量和初始状态下每个晶胞的内聚能.刘其军[3]等人计算了闪锌矿结构的GaX的电子结构和光学性质.本人也估算了GaP的ZB结构向RS结构的相变压为21.9GPa[4].

本文在刘其军[3]的基础上着重对闪锌矿结构和盐岩结构的GaP计算其电子结构并深入地对GaP的光学性质做进一步研究，因此基于密度泛函理论(DFT)的平面波理论，计算了GaP两种相的电子结构及光学性质，在相变的基础上分析了闪锌矿结构的GaP的各向异性，使其为实验研究提供理论支持.

2 计算参数和理论模型

3 理论依据

使用norm-conserving赝势，GGA-PW91法计算了GaP的光学性质,包括吸收系数、介电函数、反射率、折射指数及能量损失函数.反射系数R(ω)、介电函数的虚部ε2(ω)可以通过占据态和非占据态波函数的满足选择定则的动量矩阵元来描述，介电函数的实部ε1(ω)可以用Kramers-Kronig公式通过ε2(ω)来计算.吸收系数α(ω)、折射率n(ω)以及能量损耗函数L(ω)等其他的所有光学常数均可以由ε1(ω)和ε2(ω)推导出来.

3.1 吸收系数

吸收系数表示光波在介质中单位传播距离光强度衰减的百分比. 根据相关公式得到计算结果为[7]：

(1)

3.2 反射率

反射率R(ω)表示为：ε=ε1+iε2=N2

(2)

ε1=n2-k2ε2

(3)

根据上面三式可知[8]：

(4)

3.3 复介电函数

复介电函数反映了能带结构中导带和价带之间的跃迁.基态与时间有关的微扰论可以用来描述系统的电子与外场的相互作用.占据态和非占据态之间的跃迁包括等离激元和单粒子激发一般是由辐射场引起的.这些激发引起的谱可以由价带和导带的联合态密度来表示.介电函数作为沟通带间跃迁微观物理过程与固体电子结构的桥梁,反应了固体能带结构及其他各种光谱信息[9].因此可以通过从能带结构和态密度找出他们与介电函数实部与虚部的对应关系和联系.介电函数为：ε(ω)=ε1(ω)+iε2(ω)

(5)

用来描述介质在光子能量E=ћω的光学反应，

(6)

M表示偶极矩，i,j分别表示初末状态，fi表示第i种状态时的费米分布.ε2(ω)与固体中的基本跃迁相关，对于晶体的性质由光学跃迁过程中的动量守恒和电子密度的形式决定.也可以通过计算电子在占据轨道和非占据轨道之间的跃迁关系得到.介电函数的实部ε1(ω)可以根据Kramers-Kroning[10]关系式得到与虚部相似的计算式：

(7)

其中p表示整体的主值.

3.4 复折射率

复折射率N(ω)由折射率n(ω)和消光系数k(ω)表示，折射率可以用来描述固体宏观光学相应函数，N(ω)=n(ω)+ik(ω)

(8)

由N(ω)与ε(ω)有如下的内在联系：

ε1=n2(ω)-k2(ω)ε2=2n(ω)k(ω)

(9)

其中

(10)

(11)

3.5 能量损失函数

能量损失函数L(ω)与ε(ω)的关系如下：

(12)

3.6 闪锌矿结构GaP各向异性

通过固体的声学振动模型的长波极限可以得到Christoffel方程[11]

ρω2ui=Milul

(13)

其中ρ为密度，ω为振动角频率，ui为位移幅值，其求和写法表示笛卡尔复数.

矩阵Mil表示为：

Mil=cijklkjkk

(14)

其中cijkl是弹性张量元，kj为振动波的分矢量.

4 计算结果及讨论

经几何优化得到ZB结构和RS结构的GaP的体积与能量之间的关系，如图2由能量最小化原理可知ZB结构GaP较RS结构更稳定.

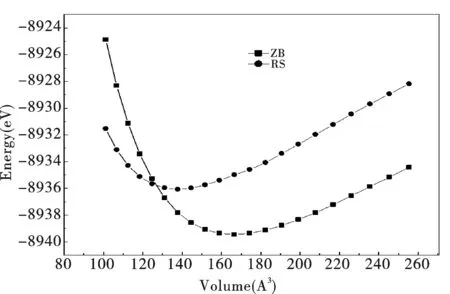
图2 能量与体积的函数Fig.2 Energy as function of the primitive cell volume for GaP

4.1RS结构GaP的能带结构及态密度分析

图3(a)—(d)分别为岩盐结构GaP的能带结构、GaP总态密度、Ga原子分态密度和P原子分态密度图.由(a)图可知岩盐结构GaP具有金属性质，其能带的价带和导带在M→G→R对称区间发生能级交错，自由电子的迁移可以使其能带被部分填充，晶体的行为表现出金属性.根据态密度(b)—(d)分析可以知道，-14eV到-9eV间的价带主要由Ga原子的3d电子贡献，其强度大小约为：74states/eV; -8到0eV间的价带主要由Ga原子4p、4s和P原子3s、3p电子轨道杂化贡献，其强度大约在0到4.7states/eV之间；费米能级附近的交错能级主要由P原子3p和Ga原子4s、4p电子轨道杂化形成；1.2到7.7eV间的导带主要由P原子3s和Ga原子4s、4p电子贡献，强度大小大约为7.4states/eV.

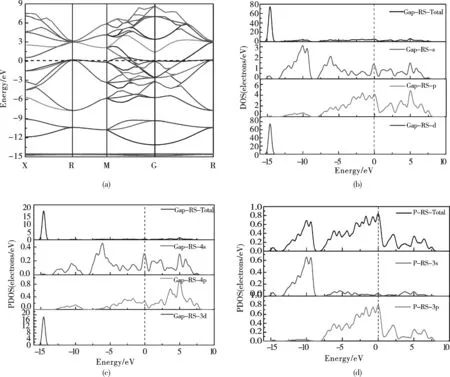
图3 (a)岩盐结构GaP能带结构图；(b)岩盐结构GaP总态密度DOS；(c)P的分态密度PDOS ；(d) Ga的分态密度PDOSFig.3 Energy band structure of the ZB structure, and the density of states for GaP,P&Ga

4.2ZB结构GaP的能带结构及态密度分析

图4(a)—(d)分别为闪锌矿结构GaP的能带结构、GaP总态密度、Ga原子分态密度和P原子分态密度图.由(a)图可知：闪锌矿结构GaP沿布里渊区高对称方向，能量零点定位费米能级处，经过分析，发现闪锌矿型GaP为间接带隙半导体(G-R)，最小带隙在第一布里渊区G点处，计算得到其带隙为：1.54eV.与参考文献[2]其算得晶格常数0.5512nm,其能隙值1.57eV更进一步证明该算法是可取的.

同时计算得到G→X，G→M，G→R的带隙分别为2.18eV,2.89eV,3.15eV.其能带除了一个或两个能带是几乎空着或者几乎充满以外，其余所有能带全部充满，晶体表现出半导体性质.与其他文献相比，本文计算的结果偏低，原因是局域密度近似(LAD)或广义梯度近似(GGA)交换关联能函数计算材料的带隙宽度或者磁耦合会低估能量，为了使结果更接近实验值或其他理论值，可以采用剪刀算符对能量进行修正.根据态密度(b)—(d)分析可以知道，-15eV到-14eV间的价带主要由Ga原子的3d电子贡献，其强度大小约为：73states/eV; -12.5eV到-9eV间的价带主要由P原子3s电子贡献，强度约为4.3states/eV；-7.5eV到0eV间的价带主要由Ga原子4s、4p和P原子3s电子贡献，峰强大约为3.9states/eV；1.54eV到10eV间的导带主要由Ga原子4s、4p和P原子3p电子贡献，峰强大约为7.9states/eV.

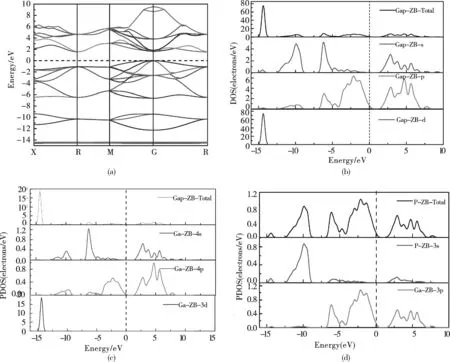
图4 (a)闪锌矿型GaP能带结构；(b)GaP的闪锌矿结构的总态密度；(c)Ga的分态密度图；(d)P的分态密度图Fig.4 Energy band structure of the RS structure, and the density of states for GaP,P&Ga

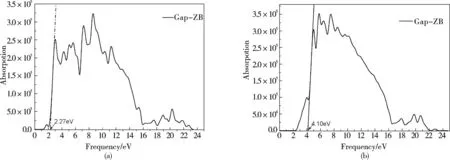
图5 GaP的RS结构与ZB结构的吸收系数Fig.5 The function of absorption coefficient for RS and ZB structures

4.3GaP的光学性质分析

图5(a)为RS结构GaP的光学吸收关系图，所对应的光子能量0eV到25eV，GaP的RS结构出现了三个吸收峰，分别用B1 ,B2 ,B3标注，它们对应的光子能量分别为：7.02eV，17.11eV，19.48eV，其中B1 ,B3峰位稍微明显，但B1的吸收率相对于B2 ,B3较大，最大的吸收峰B1吸收峰，其对应的吸收值为7.02eV.

图5(b)为ZB结构GaP的光学吸收关系图，所对应的光子能量0eV到25eV，GaP的ZB结构出现了四个吸收峰，分别用B1 ,B2 ,B3 ,B4标注，他们对应的光子能量分别为4.87eV，8.05eV，10.65eV，19.77eV.其中B2,B4峰位明显(主峰)，但B4的吸收率相对B1 ,B2 ,B3比较小，最大的吸收峰为B2 吸收峰，其对应的光子能量值为 8.05eV.在计算与取点过程中可能会造成一定的误差，可以通过剪刀算符修正得到能量对应的波长转换.

同理可得出GaP两种结构的反射率随光子能量变化曲线图.图6(a)为RS结构GaP的反射率关系图，光子能量从0eV到25eV先后出现了R1、R2、R3、R4、R5五个峰.它们分别对应光子能量的位置为：5.92eV，7.65eV，10.58eV，11.79eV，14.05eV，但这几个峰几乎不明显.图6(b)为ZB结构GaP的反射率关系图，光子能量从0eV到25eV先后出现了R1、R2、R3、R4、R5五个峰.它们分别对应光子能量为：2.62eV，4.81eV，9.06eV，11.44eV，13.48eV.其中R2与R4反射峰不是很明显，R1、R3、R5反射峰比较明显，而峰值R1、R3与R5峰值相差很大，因此R5是主峰，R1、R3是次峰，这与后面的介电函数，复折射函数图对应的比较好.

介电常数和微观的晶体轨道体系在较小波矢下对光场的线性响应由复介电常数ε(ω)=ε1(ω)+iε2(ω)的虚部ε2(ω)决定[12]，在倒易空间特殊k点位置附近的跃迁机制有密切关系，在介电常数中虚部和实部曲线上的峰值对应晶体轨道最活跃的跃迁部分.光谱是由能级间电子跃迁所产生的，各个介电峰可以通过能带结构和态密度来解释.基于第一性原理的赝势平面波方法， 我们计算出了介电函数的实部Re与虚部Im， 随光子能量变化的曲线.介电函数作为沟通带间跃迁微观物理过程与固体电子结构的桥梁，反映出固体能带结构及其他各种光谱信息.每一介电函数峰值对应一个吸收极大值，即曲线中所示的吸收峰值，表示吸收光子的能力.

介电函数实部Re在频率为0的极限情况时，由图7(a)RS结构GaP的介电函数实部曲线可以看出，在零频时的介电函数值为ε1(0)=11.18， 图中出现了一个峰值，位于2.36eV处，用D1标注，其波形变化趋势与介电函数虚部曲线相似.过了D1后曲线趋于平坦.

介电函数虚部Im，图4-3(a)中RS结构GaP的ε2(ω)在0eV至10eV之间出现了一个明显的峰值，图中用I1标注，I1位于4.35eV处，ε2的第一峰值即为吸收光子能量，其值为2.29eV.在吸收峰I1后趋于零值.

如图7(b)所示，由ZB结构GaP的介电函数实部可知，介电函数的实部出现了五个峰值，它们分别处于1.44eV，3.86eV，6.01eV，7.55eV，9.79eV位置.分别用D1，D2，D3，D4，D5标注.在零频时的介电常数ε1(0)=21.60，第一个峰值处介电函数实部ε1(ω)=28.98为最大值，所对应的光子能量为1.44eV.第二个和第五个峰它们ε1(ω)都为负值.ZB结构GaP的介电函数虚部ε2(ω)在0eV到15eV范围内出现了两个峰，当能量为2.189eV时，ε2取得第一峰值所对应的峰值为吸收最大值.在虚部曲线中包含了两个峰值，在6.46eV处出现了一个很小的峰值，这两个峰值之间所对应的ε2相差很大.它对应最高的价带到最低的导带间的子跃迁而产生.这里面不仅有电子的直接跃迁还有电子的间接跃迁，以及他们的共同作用而形成的.

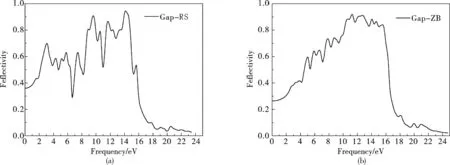
图6 GaP的RS结构与ZB结构的反射率Fig.6 The function of reflection coefficient for RS and ZB structures

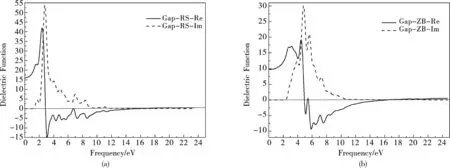
图7 GaP的RS结构与ZB结构的复介电函数Fig.7 The function of complex dielectric coefficient for RS and ZB structures

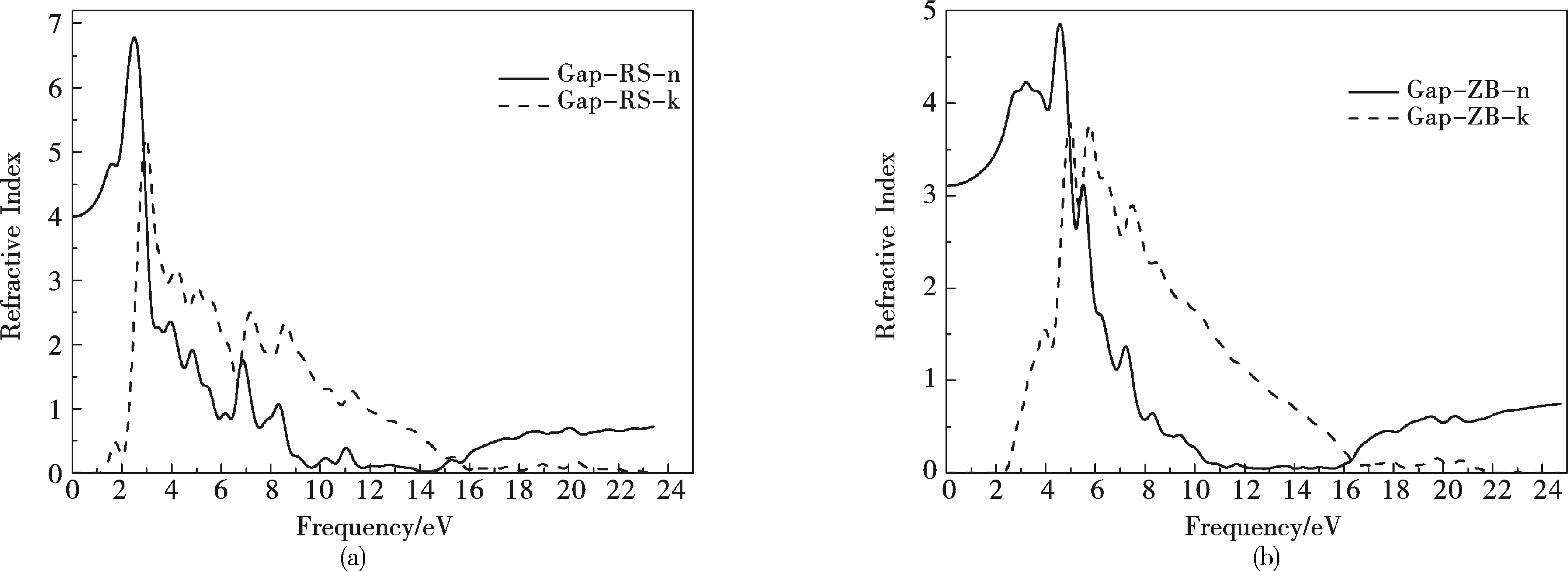
图8 GaP的RS结构与ZB结构的复折射率Fig.8 The function of complex refractive index for RS and ZB structures

通过计算可以得到岩盐结构和闪锌矿结构的GaP的复折射率曲线，图 8 (a)所示，从RS结构GaP的复折射率曲线可知，当光子能量为0eV时，n(0)=4.19，当光子能量为3.47eV时所对应的折射率n为最大值，nmax(3.47)=4.19，RS结构的GaP的折射率在整个能量范围内表现出明显的双折射性，消光系数k在带边出显示了强烈的各向异性，原因是GaP属于立方晶系，而该性质由立方晶系晶体结构特性所决定.ZB结构GaP的复折射率曲线如图8 (b)所示，当光子能量为0eV时，n(0)=4.65，当光子能量为1.54eV时，所对应的折射率n为最大值，即nmax(1.54)=5.57.可以看出ZB结构GaP的折射率在整个能量范围内表现出较RS型更明显的双折射性，随着能量的增加，在0-2.0eV范围内为正常色散.

RS结构GaP的能量损失谱共有两个峰，分别位于15.2eV，19.7eV,与前面反射率吻合得非常好.ZB结构GaP的能量损失谱也有两个峰，其中位于14.2eV峰较强，第二个峰19.8eV，这两个峰都与前面的折射率符合的很好.在能量小于1.10eV时,RS结构GaP的能量损失为0；当能量小于0.2eV时,ZB结构的GaP能量损失为0.

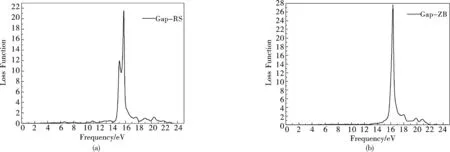
图9 GaP的RS结构与ZB结构的能量损失函数Fig.9 The function of Energy loss spectroscopy for RS and ZB structures

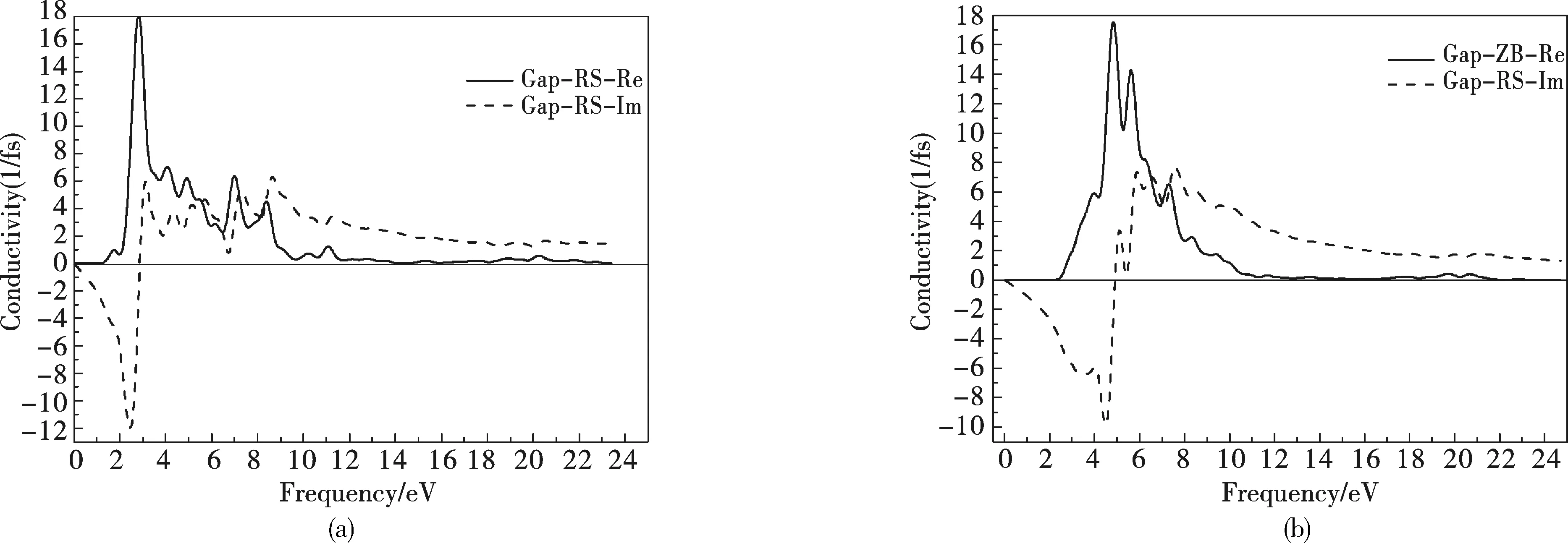
图10 GaP的RS结构与ZB结构的导电率Fig.10 The function of conductivity for RS and ZB structures

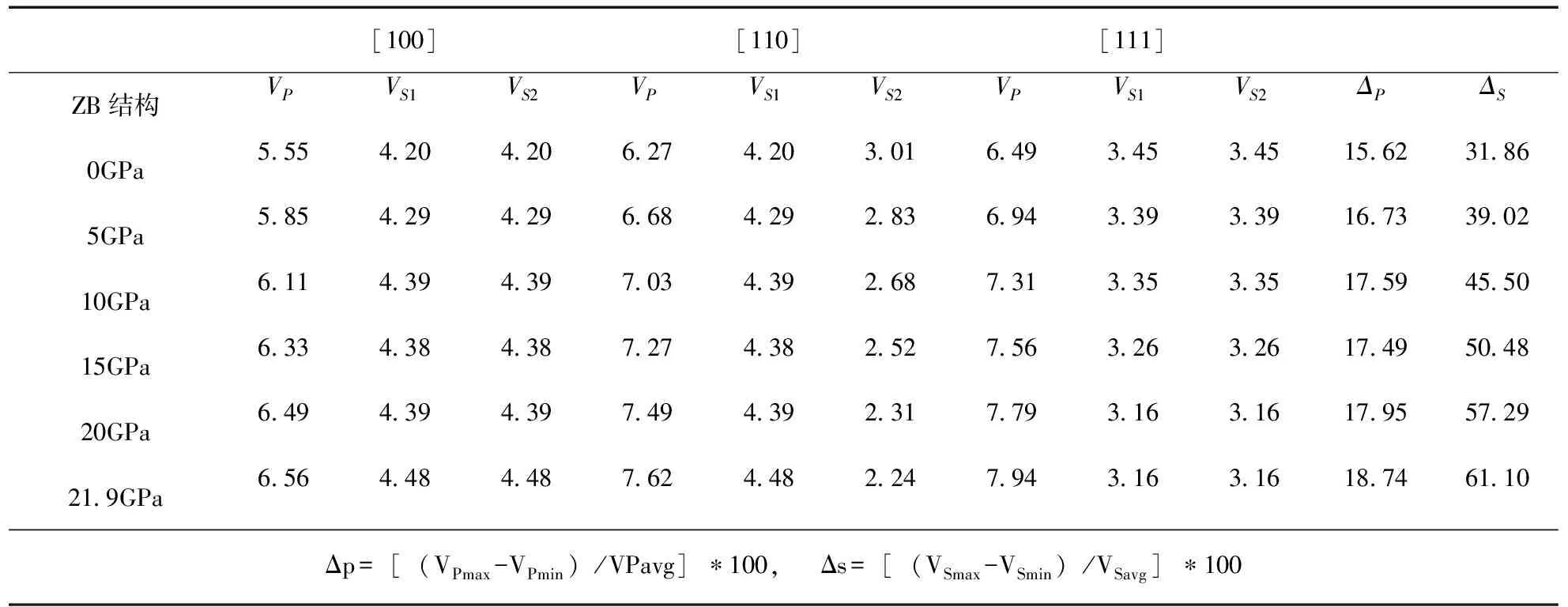
[100][110][111]ZB结构VPVS1VS2VPVS1VS2VPVS1VS2ΔPΔS0GPa5 554 204 206 274 203 016 493 453 4515 6231 865GPa5 854 294 296 684 292 836 943 393 3916 7339 0210GPa6 114 394 397 034 392 687 313 353 3517 5945 5015GPa6 334 384 387 274 382 527 563 263 2617 4950 4820GPa6 494 394 397 494 392 317 793 163 1617 9557 2921 9GPa6 564 484 487 624 482 247 943 163 1618 7461 10Δp=[(VPmax-VPmin)/VPavg]∗100， Δs=[(VSmax-VSmin)/VSavg]∗100

4.4 闪锌矿结构GaP的各向异性分析

在闪锌矿结构GaP在压强为0-21.9GPa发生相变[4]，并在这基础上计算了横波和纵波的传播速度，根据计算得到[100],[110],[111]方向传播速[13]，如表1所示.

图11为ZB结构GaP的各向异性因子随压强的变化关系：随着压强的增大，0-10GPa时各向异性因子A和Ap增加较快，压强大于10GPa时各向异性因子A和Ap增加率先降低再逐渐增高，各向异性的变化不呈线性变化.0-21.9GPa时，各向异性因子AS1和AS2随压力的增大先减小很快后缓慢较小.由此可见，ZB结构GaP是一种各向异性较强的半导体材料.

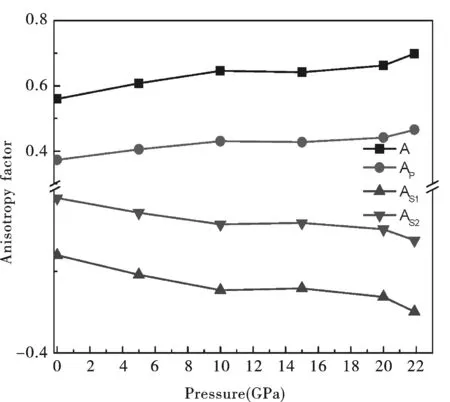
图11 ZB结构GaP的各向异性因子随压强的变化Fig.11 Anisotropy factor as a function of pressure for the ZB structure

5 结 语

本文根据能带理论初步研究了RS结构和ZB结构GaP基态下的能带结构、态密度(DOS)、分态密度(PDOS),介绍了这两种结构的能带来源。经分析发现，RS结构GaP为表现出金属性，ZB结构GaP为导体材料，其能隙为1.54eV.同时计算了这两种结构的光学性质，包括吸收系数、介电函数、反射率、折射指数及能量损失谱等，还知闪锌矿结构GaP是一种各向异性较强的半导体材料，这为GaP的实际应用提供了理论支持.

[1]JaksteS,VastN,TyuterevV.Partialfield-inducedmagneticorderinthespin-liquidKagoméNd3Ga5SiO14[J].Phys.Rev.Lett., 2007, 99： 236401.

[2] Rashid A, Fazal-e-Aleema, Javad Hashemifar S,etal. First-principles study of the structural and electronic properties of Ⅲ-phosphide[J].Phys. B, 2008, 403： 1876.

[3] Liu Q J, Liu Z G, Feng L P. First principle calculation of electronic structure and optical properties of zinc blende GaX(X=P,As,Sb)[J].JournalofUniversityofScienceandtechnologyofSuzhou(naturalscience)， 2010, 27(3)： 35 [刘其军， 刘正堂， 冯丽萍. 闪锌矿型GaX(X=P,As，Sb)电子结构和光学性质的第一性原理的计算苏州科技学院学报[J]. 苏州科技学院学报(自然科学版), 2010, 27(3)： 35]

[4] Liu L, Wei J J, An X Y，etal. Investigations of phase transition, elastic and thermodynamic properties of GaP by using the density functional theory[J].ChinsesePhysicsB， 2011, 20(10)： 106201.

[5] Madelung O, Schulz M, Weiss H. Physics of group Ⅳ elements and Ⅲ-Ⅴ compounds[J].Landout-BornsteimNewSeries, Group Ⅲ, 1987, 17(PtA).

[6] Arbouche O, Belgoumène B, Soudini B,etal. First-principles study on structual properties and phase stability of Ⅲ-phosphide (BP, Gap, Alp and Inp)[J] .Comput.Mater.Sci., 2010, 47(3)： 685.

[7] Chen K, Fan G H, Zhang Y,etal. First principles study of In-N codoped ZnO[J].ActaPhysicaSinica, 2008, 57(5)： 3138[陈琨, 范广涵, 章勇, 等. InN共掺 ZnO光学性质的第一性原理研究 [J].物理学报, 2008, 57(5)： 3138]

[8] Saha S, Sinha T P. Electronic structure, chemical bonding and optical properties of paraelectric BaTiO3[J].Phys.Rev. B, 2000, 62： 8828.

[9] Sheng X C.Spectrumandopticalpropertyofdemiconductor[M]. Beijing： Science press, 1992(in Chinese)[沈学础.半导体光谱和光学性质(第二版) [M].北京： 科学出版社, 1992]

[10] Petalas J, Logothetidis S, Gioti M,etal. Optical properties and temperature dependence of the interband transition of 3C-and 6H-SiC in the energy region 5 to 10 eV[J].Phys.Stat.Sol. B, 1998, (b)209： 499.

[11] Landua L D, Lifschitz E M, Landaou L D,etal.Courseoftheoreticalphysics:theorgofelasticity[M]. Butterworth-Heinemann, 1986.

[12] Feng J, Xiao B, Chen J C. Electronic and optical properties of CuInSe2from ab-initio calculations[J].ActaPhysicaSinica, 2007, 56(10)： 5990(in Chinese)[冯晶, 肖冰, 陈敬超. CuInSe2电子结构与光学性质的第一性原理计算[J]. 物理学报. 2007, 56(10)： 5990]

[13] Huang original, Han Ruqi adaptation.Solidstatephysics[M]. Beijing: High Education Press, 1985(in Chinese)[黄昆原著, 韩汝琦改编. 固体物理学[M]. 北京： 高等教育出版社， 1985]

First-principles study the electronic, optical properties of GaP

LIU Li1,2, WEI Jian-Jun2, TuErDi1, FENG Yan1, PENG Min1

(1.Xinjiang Institute of Engineering, Urumqi 830091, China;2.Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China)

The electronic and optical properties of zinc-blende(ZB)and rocksalt structure (RS) for gallium phosphide (GaP) are calculated by the pseudo-potential plane wave method within the generalized gradient approximation (GGA) in the frame of the density functional theory (DFT). In this work,we have preliminarily studied the band structures, density of states (DOS), partial density of states (PDOS) and introduced origin of band gap for GaP at the ground state. Combined with the band structure and density of states for the ZB and RS structure of GaP, we calculated the optical properties of GaP including absorption coefficient, reflectivity, dielectric function, complex refractive index and energy loss spectroscopy. Longitudinal and shear-wave velocities are investigated for the isotropic wave velocities to the ZB structure of GaP.

GaP; Electronic properties; Optical properties; Frist principles

103969/j.issn.1000-0364.2015.02.028

2013-7-8

新疆维吾尔自治区科技支疆项目(2013911049); 新疆工程学院博士科研启动基金项目；新疆工程学院科研基金项目(2013XGY391512)

刘丽(1985—)，女，重庆永川人，学历，硕士研究生，主要研究领域为原子分子动力学,纳米材料.

韦建军.E-mail： wjj33333@126.com

O04

A

1000-0364(2015)02-0336-09