Rashba效应对量子线中束缚磁极化子性质的影响

丁朝华, 赵 颖, 吴丽娜

(内蒙古民族大学物理与电子信息学院, 通辽 028043)

Rashba效应对量子线中束缚磁极化子性质的影响

丁朝华, 赵 颖, 吴丽娜

(内蒙古民族大学物理与电子信息学院, 通辽 028043)

采用改进的线性组合算符和幺正变换相结合的方法研究了Rashba效应对抛物量子线中强耦合束缚磁极化子性质的影响.计算了抛物量子线中强耦合束缚磁极化子的有效质量和振动频率,对RbCl材料的数值计算结果表明：量子线中强耦合束缚磁极化子的振动频率随受限强度和回旋频率的增加而增大；有效质量与磁极化子的受限强度、回旋频率和电子面密度有关,在Rashba效应影响下有效质量随上述各量的变化曲线都发生了分裂.

Rashba效应； 量子线； 磁极化子； 有效质量

1 引 言

近年来,低维量子系统性质的研究引起了国内外许多学者的广泛关注,人们采用各种方法研究了低维量子系统中磁极化子的性质[1-6].研究表明,当半导体器件规格减小到纳米尺寸时,很多宏观特性就会丧失,这时必须考虑电子的自旋特性,从而使自旋电子学成为了物理学中最热门的研究领域之一.而在低维量子系统(量子线、量子点和量子阱等)中,由于量子限制、不同方向的自旋和轨道相互作用产生的Rashba效应增大了,所以研究低维量子系统磁极化子性质时不能忽略Rashba效应的影响.张等[7-9]采用改进的线性组合算符和幺正变换相结合的方法研究了Rashba效应影响下三角量子阱中强耦合和弱耦合束缚极化子的有效质量、平均声子数等；马等[10]采用LLP中耦合的方法研究了Rashba效应对自组织量子点中强耦合极化子基态能量和激发态能量的影响；Gharaati等[11]通过解薛定谔方程来求出一维量子线中磁场和自旋轨道之间相互作用能；本文作者[12]采用改进的线性组合算符和幺正变换相结合的方法研究了Rashba效应对半导体量子线中强耦合束缚极化子性质的影响.但到目前为止,关于Rashba效应对量子线中磁极化子性质的研究甚少,本文采用改进的线性组合算符和幺正变换相结合的方法研究Rashba效应对量子线中强耦合束缚磁极化子性质的影响.

2 理论模型

设量子线在xy方向上受到抛物势的束缚,z方向上自由运动,即量子线生长方向为z方向,沿z方向施加一个均匀磁场B=(0,0,B).则考虑Rashba效应影响下,在有效质量近似下系统的哈密顿量写为：

(1)

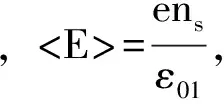
(2)

(3)

(4)

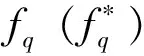
(5)

系统的总动量为：

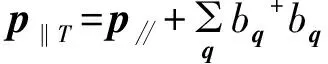
(6)

为了计算极化子有效质量,需要求U-1(H-u·p‖T)U在|Ψ>上的期待值,其中u为拉格朗日乘子,可得：

F(u,p0,λ,fq)=<Ψ|U-1(H-u·p‖T)U|Ψ>

(7)

将(7)式对fq和p0变分计算后可得：

(8)

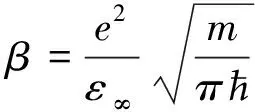
(9)

令上式方程的解为λ0,则量子线中强耦合磁极化子的基态分裂能为：

(10)

基态能量(аR=0时)为：

(11)

Rashba作用引起的附加能为：

(12)

量子线中强耦合束缚磁极化子的动量期待值为：

(13)

则量子线中强耦合束缚磁极化子的有效质量为：

(14)

上式中u为慢电子的速度.

3 结果与讨论

为了更清晰的表明量子线中强耦合束缚磁极化子的有效质量和振动频率随受限强度、回旋频率和电子面密度的变化关系,选用RbCl材料进行数值计算.所用材料的参数为[11]：ε01=4.92,ε∞=2.20,ħωLO=21.45mev,ωLO=3.39×1013S-1.数值计算结果如图1—图4所示.

图1表示磁极化子在β=2meV/s时振动频率λ随受限强度ω0和回旋共振频率ωc的变化关系曲线,由图可见,当受限强度ω0的值确定的时候,振动频率λ随回旋共振频率ωc的增加而增大,这是由于ωc的增大是外加磁场的增强导致的,外加磁场增强表示电子的能量增加,从而导致磁极化子的振动频率的增大.当ωc的值被确定的时候,振动频率λ随受限强度ω0的增大而增大,这是因为ω0增大导致受限长度减小,即电子的运动范围变窄随之电子能量增加，则振动频率就增大.

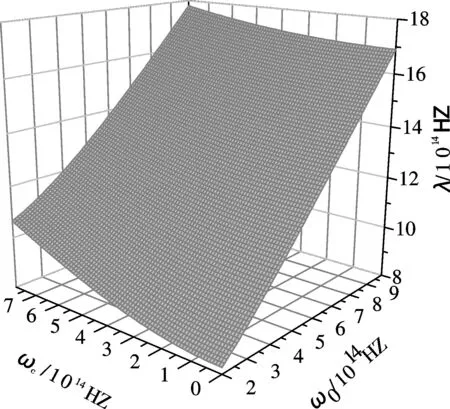
图 1 极化子的振动频率随受限强度和回旋频率的关系曲线Fig.1 The relation curves of the vibration frequency of a polaron with the confinement and cyclotron frequency

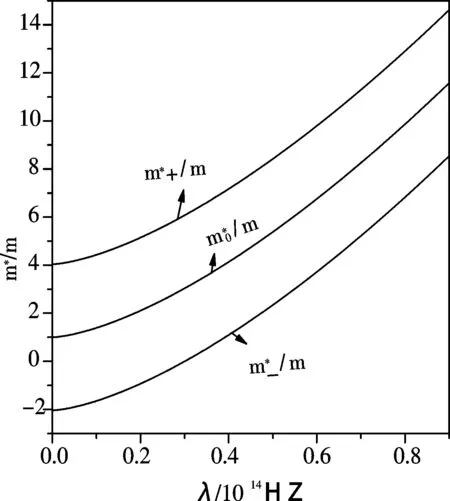
图 2 极化子有效质量比随振动频率的变化曲线Fig.2 Relation curves of the effective mass ratio changing with the vibration frequency

图3是在α=6.5的情况下得到的强耦合束缚磁极化子有效质量与电子带质量的比值随电子面密度的变化关系图.由图我们清楚的看出两条线的变化趋势相反,但变化幅度相同.当轨道和向上的自旋相互作用时磁极化子有效质量比随电子面密度的增加而线性递增；而当轨道和向下的自旋相互作用时有效质量比随电子密度的增加而线性递减.这是因为：由(14)式看出磁极化子有效质量比是Rashba自旋轨道耦合常数αR的一次函数,而αR又满足αR=C〈E〉和〈E〉=ens/ε01,所以有效质量比是电子密度的一次函数,当ns为零时αR=0,这时有效质量比不发生分裂,对应一个定值,即这时不考虑自旋和轨道之间相互作用.

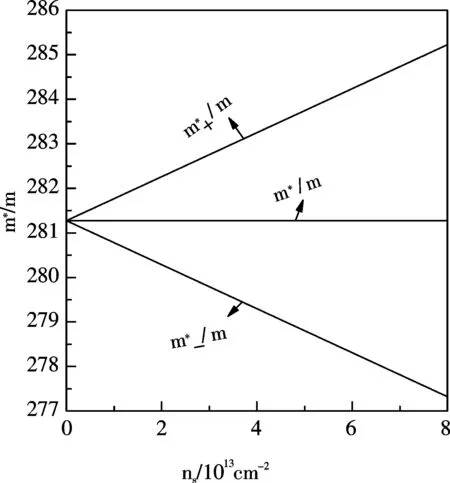
图 3 极化子有效质量比随电子面密度的变化曲线Fig.3 The relation curve of the effective mass ratio changing with the electron areal density

图 4 极化子有效质量比随受限强度和回旋频率的变化曲线Fig.4 The relation curve of the effective mass ratio changing with the confinement strengh and cyclotron frequency

图4是在α=6.5时的强耦合束缚磁极化子有效质量与电子带质量的比值随受限强度和回旋频率的变化关系曲线.由图可见,当受限强度确定时,磁极化子有效质量比随回旋频率的增加而增加,当回旋频率确定时,磁极化子有效质量比随受限强度的增加而增加,原因与图2产生原因一致.还可以看出,当回旋率取不同值时,在Rashba效应影响下,磁极化子有效质量比发生分裂,由原来的一条分裂为上下两条,分别对应于自旋向上和向下的情况,这是因为Rashba效应使能量分裂从而导致有效质量分裂.

4 结 论

本文采用改进的线性组合算符和幺正变换相结合的方法研究了Rashba效应对量子线中强耦合束缚磁极化子性质的影响.计算了量子线中强耦合束缚磁极化子有效质量和振动频率.数值计算结果表明：磁极化子振动频率随受限强度和回旋频率的增加而增大.有效质量受到Rashba效应的影响,不同方向的自旋与轨道相互作用对磁极化子有效质量的影响使有效质量分裂成几支.轨道和向上的自旋相互作用时磁极化子有效质量比随电子面密度的增加而线性递增；轨道和向下的自旋相互作用的时候有效质量比随电子密度的增加而线性递减.有效质量比随受限强度和回旋频率的增加而增加,并且也产生了分裂.

[1] Xiao J L, Ding Z H. Impurity effect of a bound polaron in quantum rods[J].J.Low.Temp.Phys., 2011, 163: 302.

[2] Ding Z H, Xiao J L. Vibrational frequency of a strong-coupling polaron in a quantum rod at finite temperatures[J].Chin.Phys. B, 2011, 20(9): 097104.

[3] Ding Z H, Sun Y, Xiao J L. Optical phonon effect in an asymmetric quantum dot qubit[J].Int.J.Quantum.Inf., 2012, 10(7): 1250077.

[4] Xie H J, Chen C Y, Ma B K. A bound polaron in cylindrical quantum wires of polaron crystal[J].Phys.Rev. B, 2001, 61: 48.

[5] Ding Z H, Zhao C L, Wu Z Y,etal. Influence of Coulomb field on properties of strong-coupling polaron in quantum wire[J].J.At.Mol.Phys., 2009, 26(6)： 1119(in Chinese)[丁朝华, 赵翠兰, 吴志永, 等. 库仑场对量子线中强耦合极化子性质的影响[J]. 原子与分子物理学报, 2009, 26(9)： 1119]

[6] He R, Ding Z H, Bao J P. Properties of excited state of bound polaron in quantum wires[J].J.At.Mol.Phys., 2011, 28(5): 949(in Chinese)[何锐, 丁朝华, 鲍继平. 量子线中强耦合束缚极化子激发态的性质[J]. 原子与分子物理学报, 2011, 28(5): 949]

[7] Zhang H R, Xiao J L. Effective mass of strong-coupling bound polaron in a triangular well Induced by Rashba effect[J].Commun.Theor.Phys., 2008, 50： 995.

[8] Zhang H R, Xiao J L. The effective mass of strong-coupling polaron in a triangular quantum well induced by the Rashba effect[J].Phys. B, 2008, 403(10-11): 1933.

[9] Zhang H R, Xiao J L. The effective mass of weak-coupling polaron in a triangular quantum well induced by the Rashba effect[J].Chin.J.Lumin., 2010, 31(1): 12.

[10] Ma X J, Xiao J L. The properties of the polaron in semiconductor quantum dots induced by influence of Rashba spin-orbit interaction[J].J.At.Mol.Sci., 2013, 4: 138.

[11] Gharaati A, Khordad R. Effects of magnetic field and spin-orbit interaction on energy levels in 1D quantum wire: analytical solution[J].OpticalandQuantumElectronics, 2012, 44(8-9): 425.

[12] Wu L N, Ding Z H, Yang Y,etal. Influences of Rashba effect on the properties of strong coupling bound polarons in quantum wires[J].Research&ProgressofSSESolidStateElectronics, 2013, 33(8): 41(in Chinese)[吴丽娜, 丁朝华, 杨杨, 等. Rashba效应对量子线中强耦合极化子性质的影响[J]. 固态电子学研究与进展, 2013, 33(8): 41]

The influence of Rashba effect on the properties of bound magnetopolaron in quantum wire

DING Zhao-Hua, ZHAO Ying, WU Li-Na

(College of Physics and Electronic Information, Inner Mongolia University for Nationalities, Tongliao 028043, China)

The influences of Rashba effect on the properties of strong-coupling bound magnetopolaron in quantum wire are studied by using the improved linear combination operator and the unitary transformation methods. The effective mass and the vibrational frequency are calculated. Numerical calculations for RbCl crystal are performed and the results show that the Rashba effect makes the effective mass of the bound magnetpolaron split into two branchs, whereas the vibration frequency λ of polaron will increase with the increases of the confinement strength and the cyclotron frequency.

Rashba effect; Quantum wire; Magnetopolaron; Effective mass

103969/j.issn.1000-0364.2015.02.020

2014-1-5

国家自然科学基金(11304143)；内蒙古自治区高校科研项目(NJZY12118)；内蒙古自然科学基金(2013MS0807)

丁朝华(1962—),女,内蒙古通辽人,教授,主要从事凝聚态光学性质的研究.E-mail: dzhaohua@126.com

O469

A

1000-0364(2015)02-0291-05