局部热力学平衡状态下的等离子体电导率计算

王竹勤， 兰 生

(福州大学电气工程与自动化学院， 福州 350108)

局部热力学平衡状态下的等离子体电导率计算

王竹勤， 兰 生

(福州大学电气工程与自动化学院， 福州 350108)

在Zollweg & Liebermann模型(Z&L模型)的基础上，结合高温条件下的量子机理作用，考虑了电子与中性粒子的碰撞关系，最终得出修正后的电导率模型，并对局部热力学平衡状态下的水中放电等离子体的粒子数密度及电导率进行了模拟计算.计算结果表明压力为定值的情况下，水中放电等离子体的总粒子数密度随温度变化呈下降趋势，温度达到15000 K时，一次电离达最大值.电导率随温度增加总体呈上升趋势，温度低于12000 K时，电子与中性粒子的碰撞起主导作用，而温度高于25000 K时，电子与离子的碰撞起主导作用.

水中等离子体； 电导率； 模拟计算

1 引 言

电导率是等离子体输运性质计算中一个重要的特性参数.为了计算电导率这一参量，Spitzer[1]最早提出了最简单实用的理想等离子体电导率公式，该公式在非理想条件下计算得到的电导率趋于无穷大，因而它仅适用于理想条件下的电导率计算.大量文献通过对非理想条件下的电导率进行修正，来研究适用于非理想条件下的电导率模型.较有代表性的两种等离子体电导率模型为Z&L模型和Mohanti & Gilligan模型(M&G模型).Z&L模型[2]修正了库仑对数，采用屏蔽半径模型，从而将Spitzer公式扩展到非理想区域.M&G模型[3]将短程力的作用考虑进去，采用更精确的非德拜屏蔽半径，并对电子态密度进行修正，得到了更为精确的等离子体的电导率模型.近年来，成剑等人[4]对比分析了Spitzer模型、Z&L模型和M&G模型这三种典型的电导率模型得到的聚乙烯电弧等离子体电导率，并将电子与中性粒子的碰撞考虑进去，所得计算模型能够较真实的反应弱非理想区域中等离子体电导率的变化；宁烨等人[5]基于Spitzer公式,初步分析了分波法计算得到的等离子体电导率与卢瑟福公式计算得到的电导率之间的区别.Aubreton等人[6]计算了不同压力情况下，水中等离子体电导率对温度的依赖性，计算结果显示电导率随温度变大且呈非线性增长趋势.Chung等人[7]研究了水中等离子体的热力学性质，模拟计算了质量密度范围为10-7至10-2，温度范围为103至105时，水中等离子体的热力学性质及电导率的变化规律.

与电弧等离子体和核聚变等离子体相比较，水中放电等离子体具有低电离度、低温、高密度、高压力，作用时间短等特点[8]，因而其电导率也具有不同的特点.在水中放电等离子体的粒子成分中，电子，H原子、O原子，H+离子、O+离子占总粒子数量的97%以上[9]，因而在电导率计算中可以忽略O原子二次以上的电离.本文对Z&L模型进行修正，考虑高温条件下的量子机理作用，同时结合电子与中性原子的碰撞因素，得到一个较简单适用的电导率计算公式.

2 电导率理论模型

水中放电等离子体的电导率由电子与周围介质的碰撞过程决定.理想条件下，等离子体完全电离，电子运动取决于电子与离子的库仑相互作用.最简单适用于理想状态下的等离子体电导率模型是Spitzer公式[1]：

(1)

式中，γ为电子间碰撞对电导率的修正系数，T为温度，Z为离子的平均电荷数，∧为库仑对数，采用下式表示：

(2)

在非理想条件下，电子与离子、电子与中性粒子的碰撞都会影响电子运动.Spitzer公式不适用于非理想条件下的电导率计算.因此，Z&L模型在Spitzer公式的基础上，对库仑对数进行修正，并采用较为合适的德拜屏蔽半径，得到适用于非理想条件下的电导率公式:

(3)

式中，∧m为修正后的库仑对数，采用下式表示：

(4)

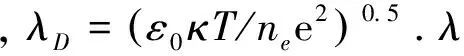
如上所示，Z&L模型将Spitzer公式扩展到非理想区域，且计算形式较简单，可在不计算等离子体非理想系数的情况下得到电导率.但Z&L模型仅考虑了电子与离子的碰撞，而忽略了电子与中性粒子的碰撞.然而，实际应用中的水中放电等离子体，电离度较低，等离子体粒子成分中仍然有H、O等中性粒子，且电子和H、O等中性粒子之间的弹性碰撞过程对于电子的能量和动量运输也起着重要作用.因此本文通过计算考虑电子与离子碰撞作用的电导率，并考虑电子与中性粒子的碰撞作用下的电导率，从而得到较为简单的电导率计算公式.

高温情况下，电子波的因素不容忽略.当电子通过圆孔时，将发生小角衍射，若该衍射角超过了经典散射角，将会增加散射导致的远距离碰撞.因而将Z&L模型与量子机理作用相结合，得到的考虑电子与离子碰撞作用的电导率如下：

(5)

其中，α为精细结构常数1/137，c为光速.

考虑电子与中性粒子的碰撞作用下的电导率如下：

(6)

综合(5)式和(6)式，非理想区域的电导率可通过下式表示：

(7)

3 模拟计算及分析

对电导率进行模拟计算前先做如下假设：

(1)水中等离子体处于局部热力学平衡状态；

(2)由于水分子、氧分子、氢分子、臭氧和多种自由基等粒子的含量较少，因而在计算中忽略以上粒子的作用;

(3)水的电离度较低，因此可忽略氧原子二次以上的电离.

3.1 粒子数密度

由电导率计算模型可知，为了模拟计算等离子体电导率随温度变化的过程，还需要知道各粒子密度和压力的数值.由假设可知水中等离子体处于局部热力学平衡状态，满足理想气体状态方程P=nκT.同时，等离子体的粒子分布满足萨哈方程：

(8)

式中，ni、Zi、Wi分别为粒子数密度、配分函数、电离势能.

忽略氧原子二次以上的电离，可利用萨哈方程导出各粒子数密度的方程.式(9)为通过萨哈方程导出的电子数密度公式：

(9)

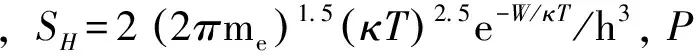
当P、T的值已知，等离子体中各类粒子数密度可通过式(8)求得.本文取压力P为定值100Mpa，离子的平均电荷数Z取1，模拟计算得到等离子体粒子数密度随温度的变化规律如图1所示.

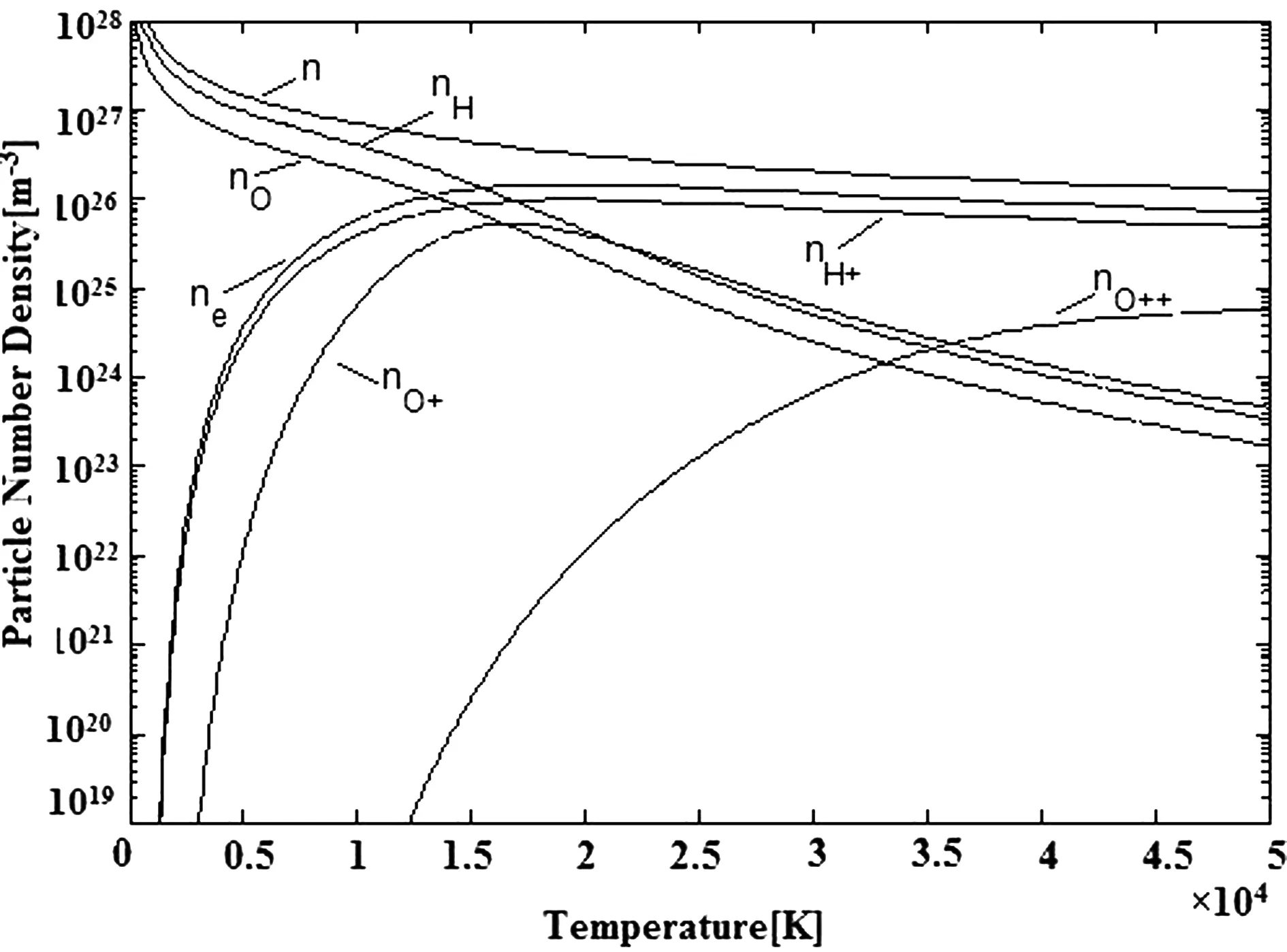
图1 压力P=100 MPa时，粒子数密度随温度的变化规律Fig. 1 The particle number density changing with the temperature for pressure of 100 Mpa

从图1可得给定压力为100Mpa的情况下，随着温度的升高，电离度增加，电离运动加剧，中性原子密度不断减少，电子和离子密度快速增长，在温度T达到15000K左右，ne、nH+、nO+出现最大值，此时一次电离达到峰值.随着温度的持续升高，ne、nH+、nO+开始出现下降趋势，原因在于等离子体中电离和复合运动同时存在，温度高于某一值后，复合运动大于分解运动.由于O离子存在二次电离，因而nO+下降速度大于nH+.图1中的n为粒子总密度，n随着温度的升高总体呈下降趋势.通过理想气体状态方程可知，压力为定值的情况下，随着温度的升高，粒子总密度应减小，且由于二次电离的关系，电子密度应比离子密度大，图1表示的结果均符合以上结论.

3.2 等离子体电导率

将通过萨哈方程求得的粒子数密度代入电导率公式，可求取相应的电导率数值.水中放电等离子体的粒子成分主要为电子，H原子、O原子，H+离子、O+离子.电子与H、O原子的碰撞截面近似取10-19m2.图2给出了考虑电子与中性粒子碰撞的电导率σen、考虑电子与离子碰撞的电导率σei及总电导率σ随温度的变化趋势。

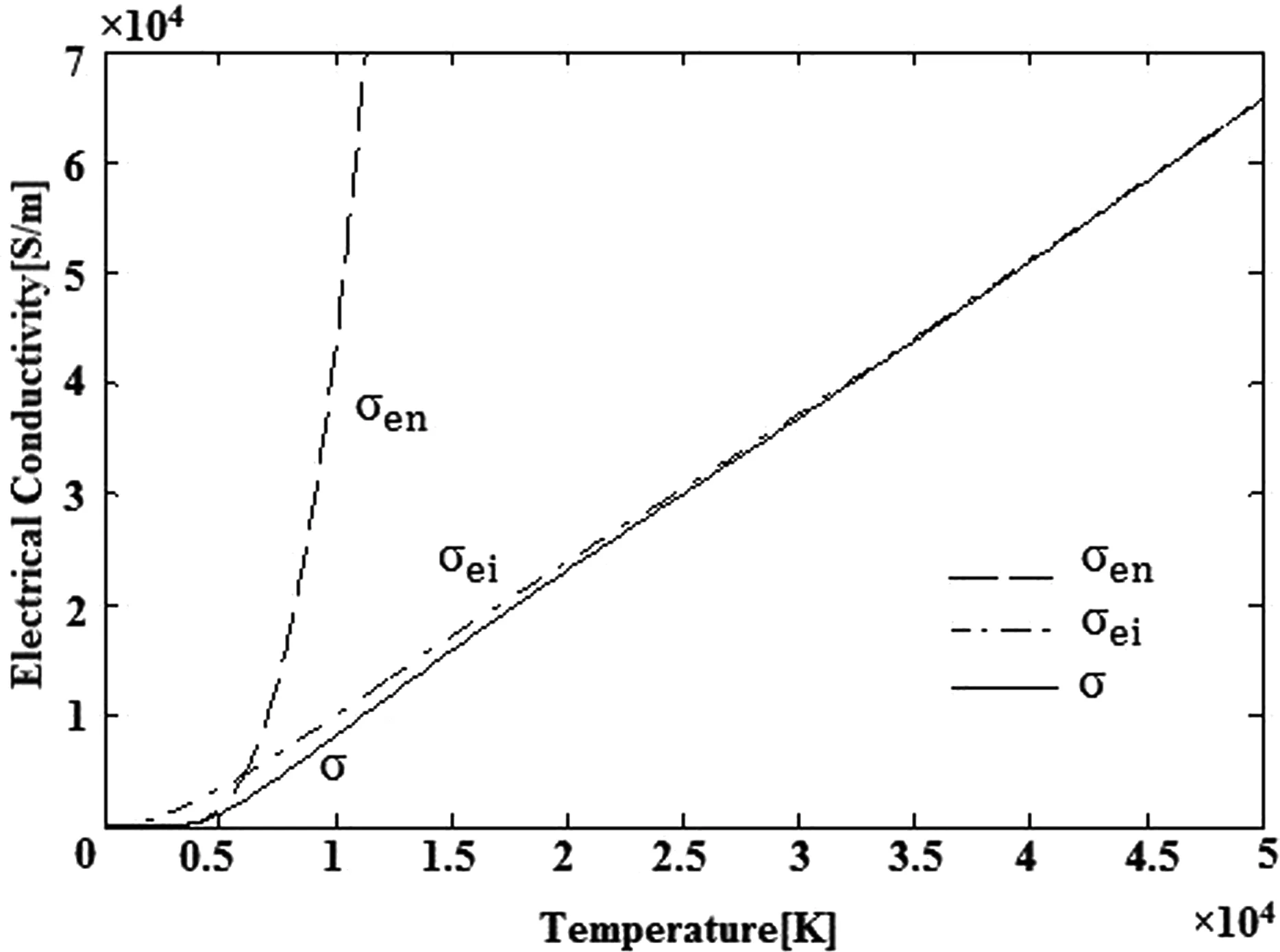
图2 压力P=100 MPa时，σen、σei及σ随温度的变化规律Fig. 2 σen, σei and σ changing with the temperature for pressure of 100 Mpa

如图2 所示，总电导率σ随着温度T的升高而变大.考虑电子与中性粒子碰撞作用的电导率σen，在较低的温度范围内随着温度的升高而变大.当温度接近10000K时，σen的增长速度突然变快.考虑电子与离子碰撞作用的电导率σei，在一定范围内随温度的升高而变大，且数值增大趋势渐缓.当温度高于25000K时，总电导率σ几乎与σei重合.分析图2可得，温度较低时，电离度较低，电子与中性粒子的碰撞起主导作用，σen不可忽略，随着温度的升高，电离度增大，中性粒子数量减少，从而电子与中性粒子的碰撞作用减弱，直至温度接近12000K时，电子与离子的碰撞作用逐渐增强.当温度高于25000K时，总电导率仅由考虑电子与离子碰撞作用的电导率σei决定.

Aubreton的电导率模拟计算结果[6]和Chung的电导率模拟计算结果[7]如图3所示.对比图2和图3可知，本文所得电导率随温度的变化趋势与Aubreton的电导率模拟计算结果和Chung的电导率模拟计算结果大致相符合，基本反映了水中放电等离子体电导率随温度的变化规律，从而验证了本文模型的正确性.与Chung的模型相比，本文修正了高温条件下电子波的影响，得到的电导率随温度变化曲线更平缓.

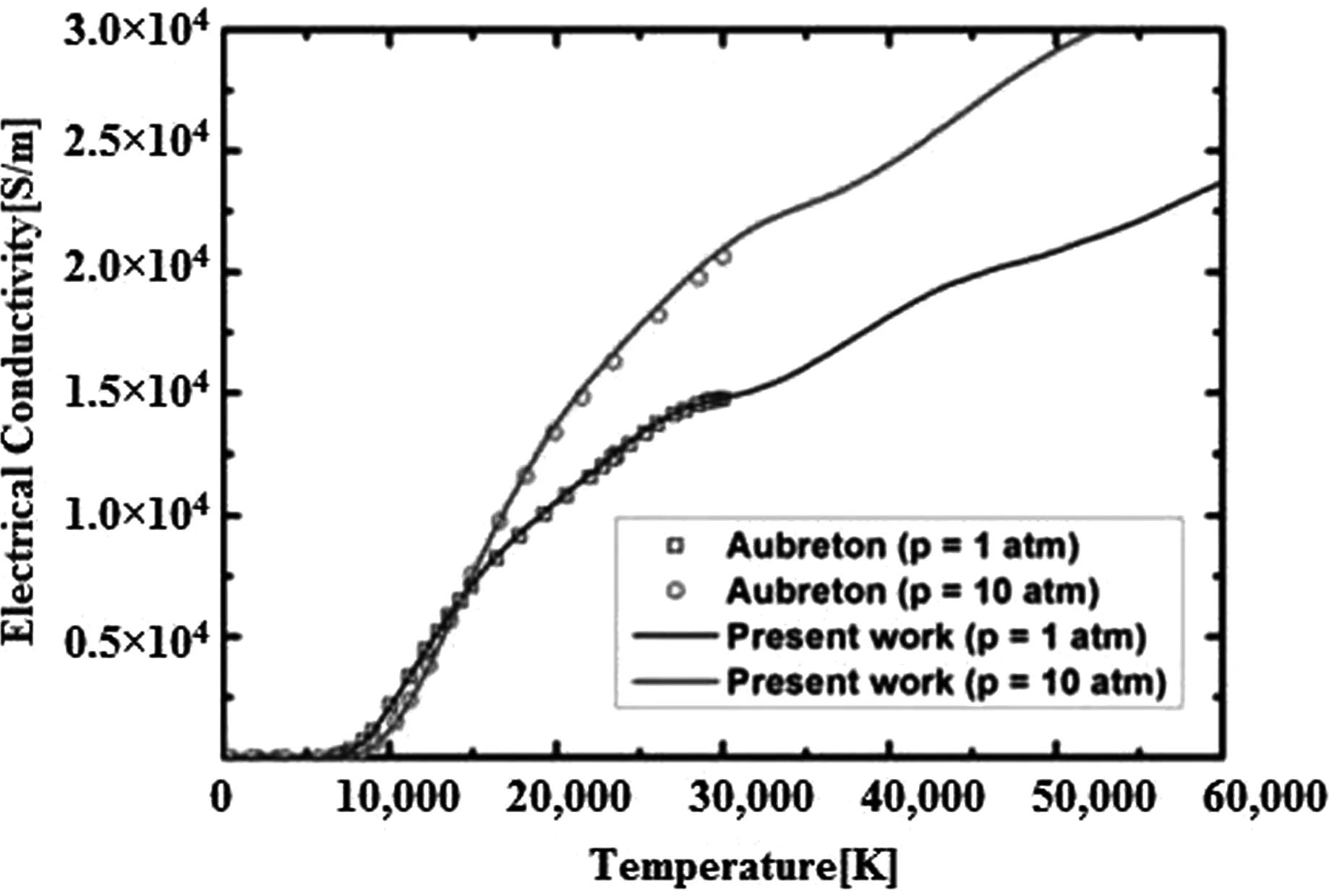
图3(a) Aubreton的电导率模拟计算结果

图3(b) Chung的电导率模拟计算结果

4 结 论

本文将Z&L模型与量子机理作用相结合，考虑电子与中性原子的碰撞作用，得出修正后的水中放电等离子体电导率模型，并对得到的电导率模型进行模拟计算.计算结果表明，电导率随温度的变化规律总体呈上升趋势，与其他文献所得结果符合度较高，验证了模型的正确性.温度较低时，电子与中性粒子的碰撞对电导率的贡献起主导作用，随着温度的升高，电子与离子的碰撞作用越来越明显.

本文求得的电导率模型简单又不失适用性，可以在不计算非理想参数的情况下得到电导率，为水中放电等离子体提供更为精确的电导率数据，为开展水中放电等离子体的综合数值模拟提供参考.

[1]SpitzerL.Physicsoffullyionizedgasses[M]. New York: Interscience, 1956.

[2] Zollweg R J, Liebermann R W. Electrical conductivity of nonideal plasmas [J].J.Appl.Phys., 1987, 62(19): 3621.

[3] Mohanti R B, Gilligan J B. Electrical conductivity and thermodynamic functions of weakly nonideal plasma [J].J.Appl.Phys., 1990, 68(10): 5044.

[4] Cheng J, Li B M.Compare and study of electrical conductivity on nonideal plasmas [J].JournalofUniversityofScienceandTechnologyofChina, 2003, 33(3): 276 (in Chinese) [成剑, 栗保明.弱非理想等离子体电导率模型比较研究 [J]. 中国科学技术大学学报, 2003, 33(3): 276]

[5] Ning Y, Yan J, Wang J G. Electron elastic scattering cross section and electrical conductivity calculation of plasma [J].J.At.Mol.Phys., 2007, (S1): 75 (in Chinese) [宁烨, 颜君, 王建国. 等离子体中电子弹性散射截面及电导率计算 [J]. 原子与分子物理学报, 2007, (S1): 75]

[6] Aubreton J, Elchinger M, Vinson J. Transport coefficients in water plasma: Part I: Equilibrium plasma [J].Plasma.Chem.Plasma.P., 2009, 29(2): 149.

[7] Chung K J, Hwang Y S. Thermodynamic properties and electrical conductivity of water Plasma [J].Contrib.PlasmaPhys., 2013, 53(4-5): 330.

[8] Lu X P, PAN Y. Theory of plasma character in a pulsed discharge in water [J].JournalofBasicScienceandEngineering, 2000, 8(3): 85(in Chinese) [卢新培, 潘垣. 水中放电等离子体特性的理论研究 [J]. 应用基础与工程科学学报, 2000, 8(3): 85]

[9] Martin E A. Experimental investigation of a high-energy density, high-pressure arc plasma [J].J.App.Phys., 1960, 31(2): 255.

[10] Qi L F, Lin Q H, Guan L,etal. Primary research of conductivity model of ablation-controlled arc plasma [J].JournalofBallistics, 2009, 21(1): 99 (in Chinese) [祁丽昉, 林庆华, 关磊, 等. 消融控制电弧等离子体电导率模型的初步研究 [J].弹道学报,2009, 21(1): 99]

Electrical conductivity simulation of plasma based on local thermodynamic equilibrium

WANG Zhu-Qin, LAN Sheng

(College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350108, China)

Based on the Zollweg & Liebermann model (Z & L model), combining with quantum mechanics which is under high temperature conditions, and considering the collisions between electron and neutral particles, the modified electrical conductivity model is accomplished, and the particle number density and electrical conductivity of water plasma are calculated under the assumption of local thermodynamic equilibrium. The results show that under certain pressure, the total particle number density of water plasma decreases when increasing temperature, and primary ionization reaches a maximum when the temperature is 15000 K. The electrical conductivity of water plasma rises when increasing temperature. When the temperature is below 12000 K, the collision of electrons and neutral particles play the leading role, while when the temperature is higher than 25000 K, the collision of electrons and ions play the leading role.

Water plasma; Electrical conductivity; Simulation

103969/j.issn.1000-0364.2015.02.014

2014-08-14

福建省自然基金(2011J01296)

王竹勤(1989-), 女,龙岩市永定县, 硕士研究生, 主要研究领域为水中放电等离子体.

兰生，副教授，硕士生导师，主要研究领域为放电等离子体.E-mail: lansheng71@163.com

O539

A

1000-0364(2015)02-0259-05