固定边界水流流场数值模拟技术的研究与实现

王朝阳

(云南水运规划设计研究院，云南 昆明 650051)



固定边界水流流场数值模拟技术的研究与实现

王朝阳

(云南水运规划设计研究院，云南 昆明 650051)

以先进的地表水流流场模拟软件SMS为平台，以金沙江陈家溪河段为研究对象，探讨固定边界水流流场数值模拟的步骤与过程，通过与实测值的对比发现，所建模型大部分监测点的水位、水深、流速的计算误差都在5%以下，表明此金沙江河段数学模型计算精度较高，可为固定边界水流研究提供借借鉴.

固定边界水流流场；数值模拟技术；SMS；水流结构

0 引 言

中国幅员辽阔、河流众多，包括山区卵砾石河流、冲积平原河流、支流交汇河口等各类相性的河流应有尽有，因此具有巨大的开发潜力和研究价值[1].

目前，常用的研究方法还是以原型观测与物理模型试验为主，但是，这两种方法具有一定的局限性，原型观测难以从一个整体的角度去研究水流动态，往往只能研究一个局部的水流形态，而物理模型试验比例尺就是一个非常头疼的问题，常常在长宽高、流速、流量、时间等因素采用正态比尺的情况下，试验场地的糙率，模型沙的直径、重度都不能很好的采用正态比尺去匹配[2]，因此只能根据经验采用相似的变态模型，导致试验结果在一定程度上失真.同时，物理模型要占用大片试验场地，耗时耗力，而模型数据则具有时效性[3-5]，容错率较低，一次测量疏忽或者数据漏测，就有可能导致试验反工重复，造成不必要的经济损失.因此，目前各高校以及科研单位都在努力开发数值模拟计算软件，以期通过建立水流平面二维模型，通过数值模拟计算来得到相应的计算结果.在此背景下，本文将以先进的地表水流流场模拟软件SMS为平台，以金沙江陈家溪河段为研究对象，探讨固定边界水流流场数值模拟的步骤与过程.

1 水流平面二维模型建立

要建立水流平面二维模型，首先要导入电子坐标底图，然后按照自定义间距生成计算网格，并把电子坐标数值离散到各网格节点上，然后再输入包括上游流量、下游水位、糙率等控制条件，形成二维水动力计算模型，检查完相应关键指标后，由二维数值计算模型程序执行计算命令，最后生成研究区域的水流平面二维流场计算结果.将水流平面二维模型建立流程示意图(见图1)，本节将结合图1，详细介绍水流平面二维模型建立.

图1 二维水动力模型工作流程

1.1 电子坐标底图导入

电子坐标底图导入是水流平面二维模型建立的首要目的，其主要目的是确定所研究领域，以及输入初始的地形高程信息，目前，SMS支持的电子坐标底图导入模式有两种：

(1)导入Tiff格式图形文件，在原底图坐标信息中随机选择三个坐标点，保证这三个坐标点在原底图与SMS文件中依次对应，从而保证SMS实际建立地形与原地形相吻合；

(2)将原底图数据直接通过CAD转换为XYZ式的三维坐标格式(Dxf文件)，然后直接在SMS软件中打开Dxf文件.

1.2 定义间距、构建网格

首先定义网格间距.一般来说，网格间距越小，计算精度越高，但计算量、计算时间也呈指数上涨，综合这两者考虑，一般将网格间距定义在10～200 m的范围内比较合适.

网格间距定义好以后，SMS软件程序会自动识别节点之间的耦合性，根据构建区域节点的规则性、密集性来形成若干的图块，图块的类型有三角形、四边形、不规则多边形三种，可在“Mesh Type”中选择网格的类型.由于三角形是最为稳定的结构，在计算机运行速度足够的情况下，尽量选择三角形网格.

最后依次在工具栏中选择“feature objects/map->2D mesh”把地图生成二维网格.

1.3 网格模型质量检查

在SMS地图生成二维网格后，为了确保计算精度以及计算迭代结果收敛，必须对网格模型质量进行检查[6-8].检查内容依次如下：

(1)三角形内角满足10°～120°范围内，四边形内角满足30°～150°范围内；

(2)两单元之间的地形最大坡度≤10%；

(3)相邻有限元的面积比是否控制在0.5～2.0之间；

(4)三角形与四边形任意两条边长度的最大比值不超过10；

(5)节点地面高程大于水面高程时，是否打开“干/湿”边界条件；

(6)为保证能量守恒，尽量使系统的边界光滑；

(7)三角形.四边形有限元是否光滑.平整；

(8)网格节点编号必须以一条边界为起始，按顺序编号，以减少计算量.

打开网格质量显示图，正常网格无颜色显示，畸形网格将呈鲜艳颜色，且随着网格质量的畸形化，其颜色也越鲜艳，依次为绿色、蓝色、紫色、红色(见图2).

图2 网格质量显示图

对于质量较差的网格，可依次做如下调整：

(1)首先将选项Nodes/Locked前面的对号去掉，以便可以任意移动节点；移动节点，直到该节点处不出现质量问题为止；

(2)修改一些明星节点高程错误，提高网格节点耦合度；

(3)在不规则区域添加部分节点，尽量使网格规则化、简单化；

(4)对于四边形单元应尽量使其长边与短边的比例增大，并使长边方向与水流方向一致.在敏感区域(如水流变化较大处)需适当增加单元数，以使网格收敛；

(5)对有质量问题的网格一直进行调整，直到不再出现网格质量问题为止.

1.4 边界条件设置与模型参数设置

(1)边界条件设置

边界条件是控制模型的初始参数，需要输入的边界条件包括：上游(模型进口)来流量与下游(模型出口)水位值，这两个参数根据实际情况将真实值输入.

(2)模型参数设置

模型参数是二维数模迭代计算的重要计算系数，模型计算参数包括：河床糙率、曼宁系数、水体密度、水体粘性系数、掺混紊动能系数，其中，水体密度一般默认为1 000 kg/m3,其他参数需要根据实际值进行率定，笔者将多年来对金沙江模型参数的研究结果(见表1).

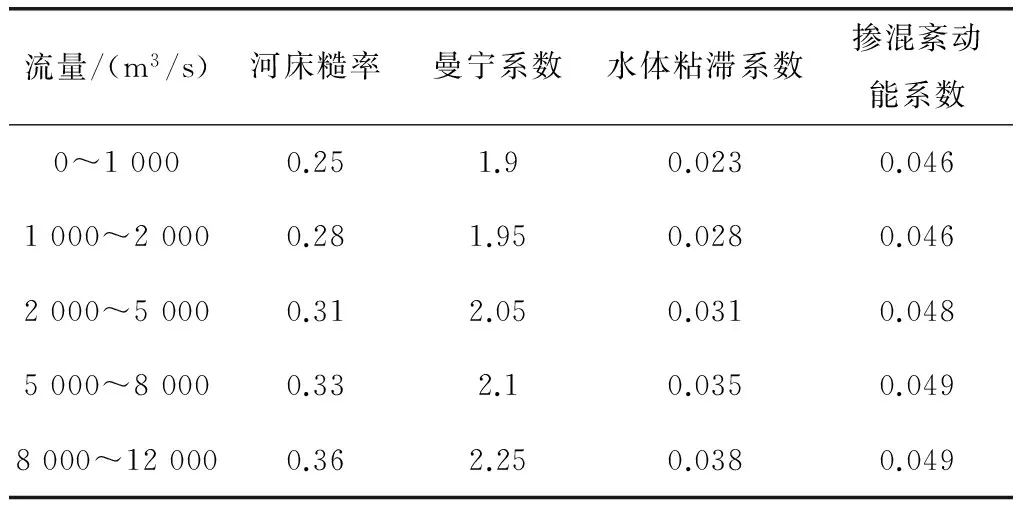
表1 金沙江各级流量下模型参数参考

1.5 模型运行

对网格进行重新编号后，便可进行模型计算.选择RMA2/Run RMA2命令进行模型计算，若模型计算结果收敛，则计算框内会出现“RMA2 finished”字样；若模型计算发散，则会出现“Stop depth convergence exceed 25.0”字样，若出现这样的情况就要对网格质量进行调整，以使二维计算模型收敛.

2 计算结果显示与输出

SMS水流平面二维数学模型可计算流场、水位、水位等水利因子信息，还可根据迭代计算结果进一步分析横向流速、水流紊动情况、水面比降、船舶自行上航动力指标等.

2.1 流场计算结果

将一年一遇洪水流量下陈家溪流场图(见图3).

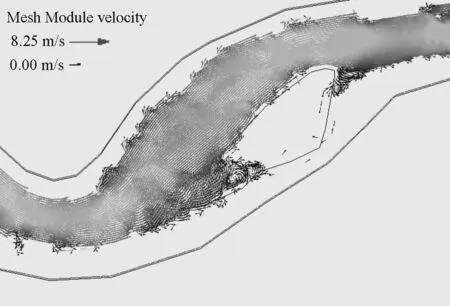
图3 陈家溪河段水流流场模拟分析

在图3中，流场线的大小以及颜色深浅均表示该点的流速大小，流场线的方向表示流速的方向，在图中右下的小图为红色矩形框内流场的放大效果图.从图3可知，SMS软件可计算水流流场情况，包括水流结构、流速大小与流速方向等等.

2.2 水位线计算结果

将一年一遇洪水流量下陈家溪水位分布图(见图4).

图4 陈家溪河段水位分布模拟分析

在图4中，颜色的深浅表示该点水位值的大小，具体可对照左上方的色板以及色板表征数值，利用研究和段水位分布模拟结果，还可以进一步推算水面比降、水面横比降等相关参数.

2.3 水深计算结果

将一年一遇洪水流量下陈家溪水深分布图(见图5).

图5 陈家溪河段水深分布模拟分析

在图5中，颜色的深浅程度表示改点的水深大小，具体可对照左上方的色板，从图5中可读出各单元点的水深值，结合之前得到的流速、水面比降等水力因子，可以进一步求得佛汝德数、断面湿周、船舶自行上航动力指标、水流紊动情况、水动力轴线等等.

3 计算结果验证

为保证数模计算精度，选择陈家溪河段五个水文监测点(SY1至SY5)作为校核取样点，对比该点的计算值与实测值，将对比结果详细(见表2).

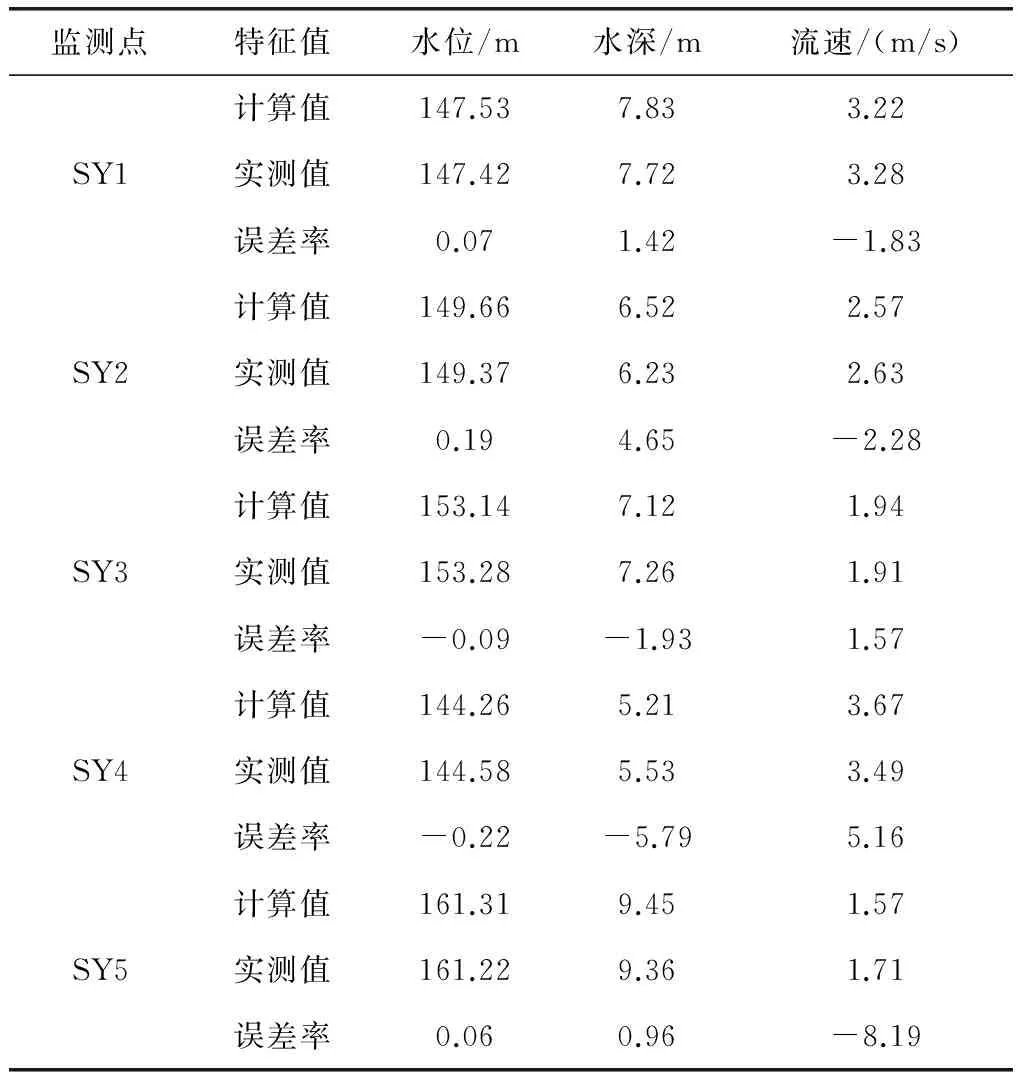
表2 计算结果精度验证

分析表2可知，大部分测点的水位、水深、流速的计算误差都在5%以下，可见本文建立的数学模型计算精度较高，可以很好的适用于金沙江河段的计算.

4 总 结

随着我国经济的迅猛发展以及国家相关部门对绿色运输的大力提倡，水运航业蓬勃发展，因此，对于固定边界水流的分析研究也愈发重要.考虑到以往的原型观测以及物理模型试验的弊端，本文考虑借鉴先进的数值模拟技术，在借助SMS二维水流数值模拟软件的基础上，以陈家溪河段为研究河段，详细的介绍了其水流平面二维数学模型建立的步骤与方法，通过与实测值的对比，本文建立的模型大部分监测点的水位、水深、流速的计算误差都在5%以下，可见本文建立的金沙江河段数学模型计算精度较高，也可见通过数值模拟的方法完全可以达到预期的研究精度，提高研究效率，节约研究经费，为固定边界水流研究提供了一种新的方法.

[1] 郭莲清.天津港码头结构综述[J].港工技术，2001(12)：63～71.

[2] 谢 龙.三峡变动回水区末端段复合水动力条件分析及对泥沙输移的影响[D].重庆：重庆交通大学.2013.

[3] 张 强，刘现鹏.岸坡土体变形对天津港高桩码头的危害[J].水道港El，2005，26(4)：241-242.

[4] 田双珠，张 勇，李越松.天津港高桩码头岸坡变形规律研究叨.水道港口，2006，27(3)：180-184.

[5] 陈 建,李义天,邓金运.汛限水位优化调度对三峡水库泥沙淤积的影响[J].水力发电学报,2012,31(1):183-188.

[6] 刘环环.薛城小沙河人工湿地水力优化研究[D].青岛:青岛理工大学,2010.

[7] 李艳红.南四湖富营养化评价及水质数值模拟研究[D].济南:济南大学：2010.

[8] 王崇宇.深水高桩码头斜顶桩驳岸结构桩土相互作用研究[D].长沙:长沙理工大学,2008.

Research and Application of Fixed Boundary Flow
Field Numerical Simulation Technology

WANG Chao-Yang

(Water Transportation Planning and Design Institute of Yunnan, Kunming 650051, China)

Many rivers in our country need further development and utilization. Using the advanced SMS simulation software of surface flow field as a platform, the steps and process of the numerical simulation for fixed boundary flow field are discussed in the this paper, taking Chenjiaxi section of Jinsha River as the research object. Compared with the measured value, the calculation errors in water level, water depth and flow velocity from the most monitoring points of the established model are below 5%. It proves that the mathematical model for Jinsha River is of high computational accuracy, providing reference for fixed boundary flow research.

fixed boundary flow field; numerical simulation technology; SMS; flow structure

2015-03-31

国家自然科学基金(50879006)

王朝阳(1980-)，男，山西忻州人，硕士研究生，主要从事港口航道、岩土工程的设计研究工作.

TV131.6

A

1008-536X(2015)09-0013-05