BEPCII储存环准直测量点位误差分析

柯志勇 何振强 董 岚 马 娜 王 铜 梁 静 罗 涛

1（中国科学院高能物理研究所 东莞分部 东莞 523803）

2（东莞中子科学中心 东莞 523803）

粒子加速器装置中，三维控制网作用十分重要。在装置建设阶段，利用控制网将各种设备精确定位安装于理论位置；在装置运行阶段，用其监测各设备的位置变化，根据偏差适时调整设备以保证加速器装置正常运行。

BEPCII的储存环是双环结构，由正电子(e+)环和负电子(e−)环组成，周长均为237.53 m，正负电子在南北两点交叉，在南交叉点进行对撞，该处安装北京谱仪(BESIII)。BEPCII储存环分4个区域，沿设备内侧隧道每隔6 m布设一组三维控制点，全环有67组共268个控制点。每组的4个控制点分别是隧道地面的A点和B点、墙上的C点和房顶的D点。储存环全环坐标系如图1所示。以S01A和S33A两个永久点的连线为X轴，正向指向S01A，两点的中点为原点，高程向上为Z轴。

图1 BEPCII储存环全环坐标系Fig.1 Coordinate system of BEPCII storage ring.

1 BEPCII储存环准直测量与数据处理方法

1.1 准直测量方法

BEPCII储存环的准直测量采用激光跟踪仪进行自由设站测量，如图2所示。储存环全环共设62站，相邻两站之间有30个左右的公共点进行搭接，保证在全环测量中每个控制点和磁铁点至少测量两遍，防止出现粗大误差，提高测量可靠性和精度[1]。

图2 BEPCII准直测量Fig.2 Alignment of BEPCII.

测量中先建立该测站的水平面坐标系，利用储存环全环理论坐标值指导测量并利用激光跟踪仪的自动定位测量功能，可大大提高测量效率。测完该站后利用实测值与全环理论值的拟合偏差作为该站测量的外符合精度检验，利用该测站的两遍 BPM (Beam Position Monitor)测量值的拟合偏差作为内符合精度检验，并用该站与上一站的公共点搭接拟合精度来检核该测量数据的偏差值，从而对测量的累积误差进行控制。在各项检核的结果符合要求后，将测站水平坐标系下的测量数据作为测后平差计算的原始数据。利用该测量方法完成全环62站的测量工作和数据检验。

1.2 测量数据平差处理方法

BEPCII储存环准直测量数据按平面和高程分别进行平差处理。数据先用高能所自主开发软件verctor计算相邻两测站和总体数据的边角差和坐标差，删除测站数据中有粗大误差的测量点[2]。再将所有测站数据拟合归化到首站的测站水平坐标系中，用SURVEY软件将总体数据在储存环全环理论值为参考下进行平差计算，基准点S01A和S33A的平面坐标为已知，设置边长和角度中误差为verctor软件计算的总体数据的测边和测角误差几何平均值，经计算可得到平面平差结果及误差。

高程平差采用清华山维软件 EpaNas将各点数据进行观测值等级为国家二等的高程平差计算，基准点为S01A，经计算可得到高程平差结果及误差。

2 点位误差计算方法

2.1 绝对点位误差计算方法

在 BEPCII储存环控制网中，往往需要关心点位最大误差和最小误差的方向及点位在储存环全环坐标系下的径向误差和切向误差，而利用误差椭圆可以精确形象地反映待定点的点位在各个方向上的误差分布情况[3]。

误差椭圆的长半轴即误差极大值 E、短半轴即误差极小值F及长半轴方位角jE称为误差椭圆的三要素。如图3所示，由椭圆圆心向y方向引一射线，垂直于y方向上作椭圆的切线，则垂足与原点的连线长度就是y方向上的位差sy，有：

图3 误差椭圆Fig.3 Error ellipse.

对于环形控制网测量数据，如果已知该待定点的误差椭圆，则根据式(1)可得径向误差sr及切向误差st为：

式中，O为环形网原点；αOP为原点O与P点连线的方位角，αOP在0°−360°之间。

BEPCII储存环坐标系中，对于方位角αOP，有：

式中，xP、yP为P点的平面坐标。

BEPCII储存环准直测量数据的平差结果中给出了各控制点的误差椭圆三要素和平面坐标，则可根据上述公式求出控制点的径向绝对点位误差和切向绝对点位误差。

2.2 相对点位误差计算方法

误差椭圆只能确定已知点与待定点之间位置的精度，在工程应用中，往往更关心两个待定点之间的相对位置精度关系[4]，特别是对于粒子加速器装置的控制网，相邻两点间的相对点位误差，是保证粒子加速器设备的安装和调整精度从而保证粒子轨道的平滑性的关键因素[5]。通常用相对误差椭圆来描述两待定点间的相对位置精度关系。同样可根据平差结果中给出的两点间相对误差椭圆三要素及点位平面坐标求出控制点的径向相对点位误差和切向相对点位误差。

3 控制网点位误差统计及分析

3.1 先验误差

先验误差是控制网测量值平差前对测量值的测量误差的估计值，其对数据平差结果和精度统计至关重要，通常用仪器的标称精度来确定先验误差，但仪器标称精度与数据实际测量精度并不相符。BEPCII储存环准直测量数据平差前的先验误差通常用仪器实际的测边精度和测角精度的几何平均值来确定，即用大量实测数据的边角差的几何平均值来确定。

据BEPCII储存环2006−2012年隔年的准直测量数据，各年的边角差并统计数据如表1所示。

表1 BEPCII储存环准直点测量数据边角误差Table 1 Distance and angle measurement error in alignment of BEPCII storage ring.

由表1的边角差数据可知，各年数据的斜距差在0.5 mm以内，对于2006年数据，因其当时储存环环境不稳定且准直测量共设39站，测距范围比其它三年要大，因而斜距差较大。其他三年的准直测量共设62站，斜距差几何平均值基本在0.10 mm以内，可反映激光跟踪仪测距比较稳定。经计算，每站测点的平均斜距为5 m左右，测距精度为0.07 mm左右，测角误差为3″左右，考虑到仪器自身精度、隧道环境、反射镜误差等因素的影响，该测距和测角精度能够真实反映激光跟踪仪的实际测量精度。各年SURVEY平面平差结果中，单位权验前验后比值m0分别为0.91、1.07、1.00和1.00，表明先验误差与验后误差很接近。

3.2 绝对点位误差

根据2006−2012年隔年的BEPCII储存环控制网平差结果，选取具有代表性的A线控制点（靠近加速器设备的一圈地面控制点），计算得出各年的绝对点位中误差如图4(a−c)和表2所示。

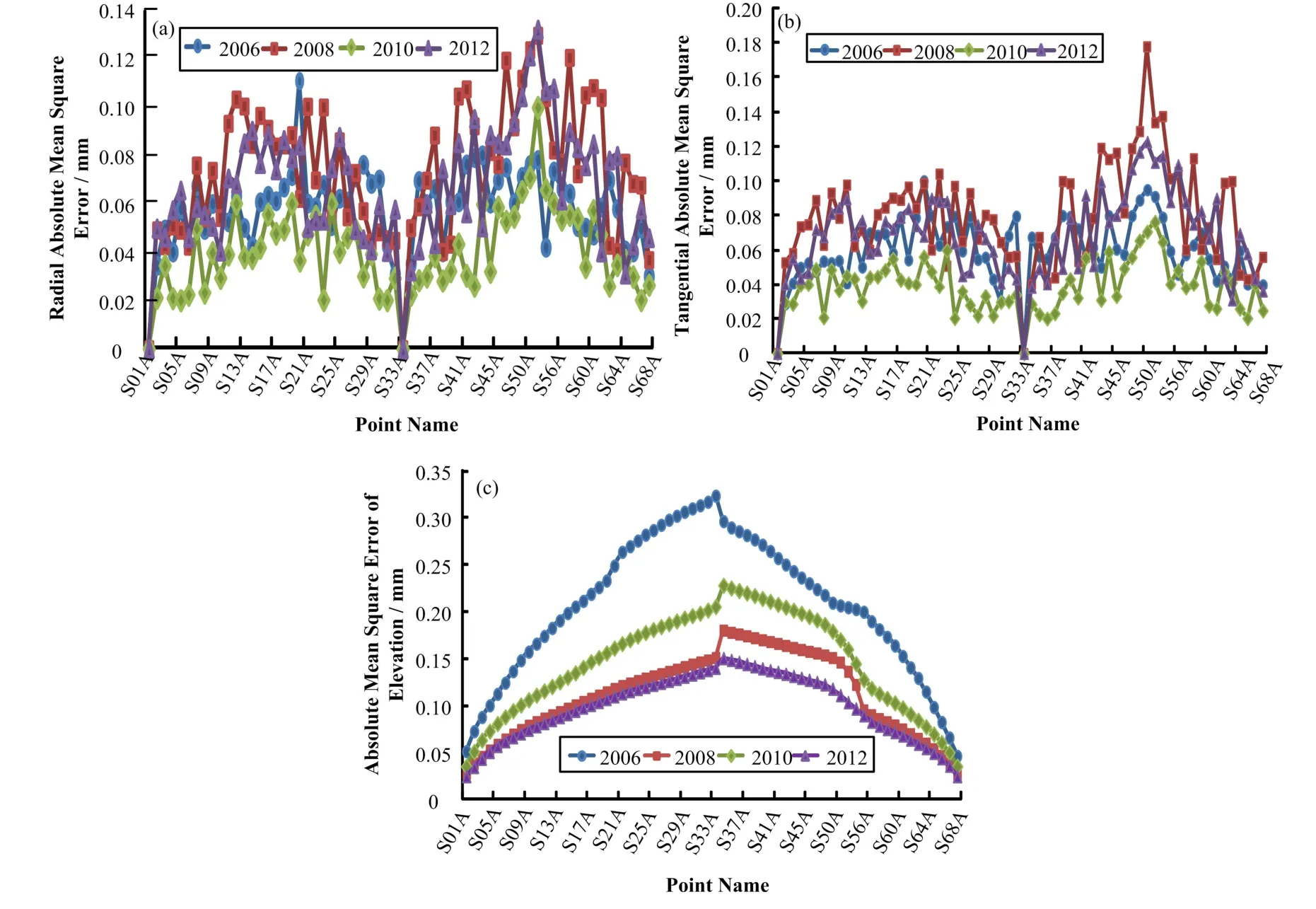
图4 BEPCII储存环A线各控制点绝对点位中误差平面径向(a)、切向(b)和高程方向(c)绝对点位中误差Fig.4 Absolute mean square error of the control points A in BEPCII storage ring. (a) Radial, (b) Tangential, (c) Elevation

表2 BEPCII储存环控制网A线控制点绝对点位中误差(mm)Table 2 Absolute mean square error of the control points A in BEPCII storage ring (mm).

由图4和表2中绝对点位误差数据可知， A线控制点的径向和切向绝对点位中误差基本相同，且它们的几何平均值均在0.07 mm左右，0.10 mm以内；高程绝对点位中误差的几何平均值在0.12 mm左右，0.25 mm以内，远优于BEPCII储存环平面控制网径向绝对点位中误差小于0.5 mm的指标。

对于平面绝对点位中误差，各点数值与几何平均值的偏差量在0.05 mm左右，因平面基准点S01A和S33A的绝对点位误差为零，绝对点位误差曲线成M形；高程平差以S01A为基准点，对于闭合控制网，高程绝对点位误差从 S01A两侧向中间点S33A累积，导致S33A的误差最大。

3.3 相对点位误差

根据2006−2012年隔年的BEPCII储存环控制网平差结果，计算得出控制点A点每年的相邻两点相对点位中误差如图5(a−c)和表3所示。

图5 BEPCII储存环A线各控制点平面径向(a)、切向(b)和高程方向(c)的相对点位中误差Fig.5 Relative mean square error of the control points A in BEPCII storage ring. (a) Radial, (b) Tangential, (c) Elevation

表3 BEPCII储存环控制网A线控制点相对点位中误差(mm)Table 3 Relative mean square error of control points of line A in BEPCII storage ring (mm).

由表3可知，控制网A点的径向、切向和高程相对点位中误差的几何平均值均在0.05 mm左右，0.06 mm以内，说明BEPCII储存环控制网网型较好，设计合理，相对点位精度比较高，且优于平面控制网径向相对点位中误差小于0.15 mm的指标。

由本文误差统计及分析，得到以下结论：

(1) 激光跟踪仪的实际测量精度为：5 m测距精度为0.07 mm左右，测角精度为3″左右；

(2) 利用测量数据统计的边角差的几何平均值能够很好反映仪器的实际测边和测角精度，可以作为数据平差时的先验误差。

(3) BEPCII储存环控制网的径向和切向绝对点位中误差的几何平均值均在0.07 mm左右，高程的在0.12 mm左右；径向、切向和高程相对点位中误差的几何平均值均在0.05 mm左右。

4 结语

介绍了 BEPCII储存环准直测量方法和数据平差处理方法，对近四年 BEPCII储存环测量数据进行平面和高程独立平差处理的结果，计算出控制网A点平面径向、切向和高程的绝对点位中误差和相邻两点相对点位中误差，并对相关误差进行了分析。数据表明，BEPCII储存环准直测量的点位精度较高，均优于BEPCII设计指标，可为ADS (Accelerator Driven System)、CEPC (Central Electric Power Cooper)等其它加速器装置的控制网的设计和测量提供参考依据。

1 于成浩, 柯明. 基于激光跟踪仪的三维控制网测量精度分析[J]. 测绘科学, 2006, 30(3): 25−27

YU Chenghao, KE Ming. The measurement accuracy analysis of three dimensional control network based on laser tracker[J]. Science of Surveying and Mapping, 2006, 30(3): 25−27

2 梁静, 董岚, 罗涛, 等. BEPCII储存环激光跟踪仪测量精度统计及先验误差的确定[J]. 测绘科学, 2013, 38(6): 182−184

LIANG Jing, DONG Lan, LUO Tao, et al. Precision statistic of laser tracker in BEPCII storage ring and calculation of mean square error of unit weight[J]. Science of Surveying and Mapping, 2013, 38(6): 182−184

3 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 第二版. 武汉: 武汉大学出版社, 2009: 185

Surveying and Adjustment Team in School of Geodesy and Geomatics of Wuhan University. Error theory and foundation of surveying adjustment[M]. 2ndEd. Wuhan: Wuhan University Press, 2009: 185

4 卞和方, 张书毕, 李益斌, 等. 误差椭圆在精密工程测量中的应用研究[J]. 海洋测绘, 2009, 29(1): 49−51

BIAN Hefang, ZHANG Shubi, LI Yibin, et al. The application research on error ellipse in precision engineering survey[J]. Hydrographic Surveying & Charting, 2009, 29(1): 49−51

5 于成浩, 柯明, 杜涵文, 等. 三维控制网技术在BEPCII储存环中的应用研究[J]. 高能物理与核物理, 2006, 30(11): 1107−1112

YU Chenghao, KE Ming, DU Hanwen, et al. Application research of 3D control network technology in BEPCII storage ring[J]. High Energy Physics & Nuclear Physics, 2006, 30(11): 1107−1112