关于亚循环2群的LA猜想
2015-03-22张慧玲
白 颉, 张慧玲
(太原学院 数学系, 太原 030001)
白 颉*, 张慧玲
(太原学院 数学系, 太原 030001)
LA猜想是有限p群中一个著名的猜想. 该文依据亚循环2群的分类,通过计算有循环极大子群、无循环极大子群的通常亚循环2群及例外亚循环2群的自同构群的阶,证明了亚循环2群满足LA猜想,并圆满地回答了亚循环p群满足LA猜想这一问题.
p群; 亚循环2群; 自同构群; 阶; LA猜想
有限群的自同构群是有限群中一类非常重要的群,许多学者致力于自同构群阶的研究,并取得了丰硕的成果. 文献[1]计算了|G′|=p的自同构群的阶;文献[2-10]给出了某些小阶群的自同构群的阶;对一般的有限p群,G.Birkhoff和P.Hall于1933年在文献[11]给出了其自同构群阶的最佳上界,但其下限至今仍未解决,即著名的LA猜想:设G是有限非循环p群,|G|=pn,n>2,则|G| |Aut(G). 早在1970年,Davitt 在文献[12]中证明了亚循环p(p≠2)群满足LA猜想,但对亚循环2群是否满足这一猜想,一直悬而未决. 文献[13]给出了亚循环2群的分类,借助于该分类,下面通过计算各类亚循环2群的自同构群的阶证明了LA猜想对该群是成立的, 从而圆满回答了亚循环p群是否满足LA猜想的问题.
本文沿用文献[13]的术语,其它符号和术语都是标准的.
1 预备知识
定义称G为亚循环群,如果G有循环正规子群N,使商群G/N也是循环群,即亚循环群为循环群被循环群的扩张.
引理1[13]设G为亚循环2群,若G无循环极大子群,则G有两种类型:
(i)通常亚循环群:G=〈a,b|a2r+s+u=1,b2r+s+t=a2r+s,ab=a1+2r〉,其中,r,s,t,u是非负整数,且r≥2,u≤r. 通常亚循环群可裂当且仅当stu=0.
(ii)例外亚循环群:G=〈a,b|a2r+s+v+t′+u=1,b2r+s+t=a2r+s+v+t′,ab=a-1+2r+v〉,其中,r,s,v,t,t′,u是非负整数,满足r≥2,t′≤r,u≤1,tt′=sv=tv=0,且若t′≥r-1,则u=0;例外亚循环群可裂当且仅当u=0.
引理2[14]设G是有限p群,G=〈a,b〉,φ∈Aut(G),其中,φ:a→bjai,b→bsar,则G=〈aφ,bφ〉⟺is-jr≡/ 0(modp).
引理3[15]设n是正整数,n≥2,令U=U(2n)是环Z/2nZ的可逆元组成的乘法群,则
U=〈-1〉×〈1+2n〉(≅G2×G2n-2)= {ε+i2m|ε=1或-1, 2≤m≤n,
1≤i<2n-m,且i是奇数},
又对m 引理4设G是群,a,b∈G,i,j,r,n为整数.若ab=ar,则 (i) (ba)n=bna1+r+…+rn-1; (ii)aibj=bjairj. 引理5设G是亚循环p群,|G′|=pn. 则 (i) 当p≠2时,G是pn交换的; (ii) 当p=2时,G是2n+1交换的,但不是2n交换的. 证明 (i) 由文献[15]中第167页的引理6.2.4可得. (ii)任取x,y∈G,则由文献[15]中命题2.1.8可得, 引理6设G为无循环极大子群的通常亚循环2群,即 G=〈x,y|x2n=1,y2m=x2k,xy=x1+2l〉,i,j为整数,若2|i或2|j,则(yjxi)2n-l=yj2n-lxi2n-l. 证明令H=〈xi,yj〉,其中,i=2si′,j=2tj′,s和t至少有一个不为0,则H′=〈[xi,yj]〉.由于(1+2l)j≡1(mod 2l+t),故可设(1+2l)j=1+k2l+t, (k,2)=1,于是[xi,yj]=xki2l+t=xki′2l+s+t,故H′=2n-l-s-t,由引理5知H至少是2n-l交换的,故(yjxi)2n-l=yj2n-lxi2n-l. 本节将依次给出有循环极大子群、无循环极大子群的通常亚循环2群及例外亚循环2群的自同构群的阶,同时证明亚循环2群满足LA猜想. 定理1设G是有循环极大子群的亚循环2群且G非循环,则 (1) 若G≅G2n-1×G2,则|Aut(G)|=2n; (2) 若G≅M2(n-1,1),n≥4,则|Aut(G)|=2n; (3) 若G≅Q2n,n≥3,则|Aut(G)|=24(n=3),|Aut(G)|=22n-3(n≠3); (4) 若G≅D2n,n≥3,则|Aut(G)|=22n-3; (5) 若G≅SD2n,n≥4,则|Aut(G)|=22n-4. 证明由文献[15]中第二章定理2.2.10可知G为下列群之一:G2n-1×G2;M2(n-1,1),n≥4;Q2n,n≥3;D2n,n≥3;SD2n,n≥4. 简单计算易知:若G≅G2n-1×G2,则|Aut(G)|=2n;若G≅M2(n-1,1),n≥4,则|Aut(G)|=2n;若G≅Q2n,n≥3,则|Aut(G)|=24(n=3),|Aut(G)|=22n-3(n≠3);若G≅D2n,n≥3,则|Aut(G)|=22n-3. 下证(5). 设G=〈a,b|a2n-1=1,b2=1,b-1ab=a-1+2n-2〉,n≥4,φ:a|→bjai,b|→bsar是G的变换,则φ∈Aut(G)⟺i,j,r,s满足关系式:j=2,s=1,(i,2)=1,r为偶数,1≤i,r≤2n-1. 事实上,若φ∈Aut(G),则〈bjai,bsar〉=G,1≤i,r≤2n-1,j,s=1或2,且bjai、bsar满足与a、b相同的定义关系.首先断言s=1,否则,由o(b)=2知:b→ar且r=2n-2.于是G=〈bjai,a2n-2〉,又由于a2n-2∈Z(G),故可得G为交换群,矛盾.再由(bar)2=barbar=ar2n-1=1得,r为偶数.由于G中元素除〈a〉外,要么为2阶元,要么为4阶元,且n≥4,故j=2,(i,2)=1.反之,若i,j,r,s满足上述关系式,由引理2知〈bjai,bsar〉=G,又bjai、bsar满足与a、b相同的定义关系,故φ∈Aut(G).于是|Aut(G)|等于满足上述关系式的i,j,r,s的各种可能的取法,即|Aut(G)|=22n-4. 定理2设G是无循环极大子群的通常亚循环2群且G非交换,即G=〈a,b|a2r+s+u=1,b2r+s+t=a2r+s,ab=a1+2r〉,其中,r≥2,u≤r. (i) 若stu=0,则|Aut(G)|=24r+2s+t-1; (ii) 若stu≠0,则|Aut(G)|=24r+2s+t. 证明设φ:a→bjai,b→bnam,对于(i)分下面(a)、(b)、(c)三种情况来论证: (a) 若u=0,此时G=〈a,b|a2r+s=1,b2r+s+t=1,ab=a1+2r〉,下证φ可以扩充为G的自同构的充要条件是i,j,m,n满足关系式:(i,2)=1,j≡0(mod 2s+t),n≡1(mod 2s), 1≤i,m≤2r+s, 1≤j,n≤2r+s+t. 事实上,若φ可以扩充为G的自同构,则〈bjai,bnam〉=G,1≤i,m≤2r+s,1≤j,n≤2r+s+t,且bjai、bnam满足与a、b相同的定义关系.由引理2知in-jm≡/ 0(mod 2).由引理4知, (bjar)bnam=bja-m(1+2r)j+i(1+2r)n+m,且(bjai)1+2r=bj(1+2r)ai[1+(1+2r)j+…+(1+2r)j2r].由引理1(i)知G可裂,于是有 故j≡0(mod 2s+t),从而(i,2)=(n,2)=1. 又由引理3 知,(1+2r)j≡1(mod 2r+s+t),故i(1+2r)n≡i(1+2r)(mod 2s+r),于是n≡1(mod 2s). 反之,若i,j,m,n满足上述关系式,易证〈bjai,bnam〉=G,且bjai、bnam满足与a、b相同的定义关系,从而φ可以扩充为G的自同构. 可见|Aut(G)|等于满足上述关系式的i,j,m,n的各种可能的取法. 因i有2r+s-1种取法,j有2r种取法,m有2r+s种取法,n有2r+t种取法,故|Aut(G)|=24r+2s+t-1. (b) 若u≠0,t=0,此时G=〈a,b|a2r+s+u=1,b2r+s=a2r+s,ab=a1+2r〉. 令ba2u-2r-1-1为新b,可将G转化为〈a,b|a2r+s+u=1,b2r+s=1,ab=a1+2r〉. 下证φ可以扩充为G的自同构的充要条件是i,j,m,n满足关系式: (i,2)=1,j≡0(mod 2s), m≡o(mod 2u),n≡1(mod 2s+u), 其中,1≤i,m≤2r+s+u,1≤j,n≤2r+s. 事实上,若φ可以扩充为G的自同构,则〈bjai,bnam〉=G,1≤i,m≤2r+s+u,1≤j,n≤2r+s,且bjai、bnam满足与a、b相同的定义关系.由引理2知,in-jm≡/ 0(mod 2).由o(bnam)=2r+s知,m必为偶数(若否,则o(bnam)=2r+s+u). 于是由引理6知,m≡0(mod 2u). 由引理4知, (bjai)bnam=bja-m(1+2r)j+i(1+2r)n+m,且(bjai)1+2r=bj(1+2r)ai[1+(1+2r)j+…+(1+2r)j2r]. 由引理1(i)知G可裂,于是有 故j≡0(mod 2s),从而(i,2)=(n,2)=1.又由引理3知,(1+2r)j≡1(mod 2r+s),故i(1+2r)n≡i(1+2r)+ik2r+s(mod 2r+s+u),其中,k∈Ζ,于是n≡1(mod 2s+u). 反之,若i,j,m,n满足上述关系式,易证〈bjai,bnam〉=G,且bjai、bnam满足与a、b相同的定义关系,从而φ可以扩充为G的自同构. 可见|Aut(G)|等于满足上述关系式的i,j,m,n的各种可能的取法. 因i有2r+s+u-1种取法,j有2r种取法,m有2r+s种取法,n有2r-u种取法,故|Aut(G)|=24r+2s-1. (c) 若u≠0,t≠0,s=0,此时G=〈a,b|a2r+u=1,b2r+t=a2r,ab=a1+2r〉. 令b为新的a,ab-2t为新b,可将G转化为〈a,b|a2r+t+u=1,b2r=1,ab=a1+2r+t〉.下证φ可以扩充为G的自同构的充要条件是i,j,m,n满足关系式: (i,2)=1,m≡0(mod 2t+u), n≡1(mod 2u), 1≤i,m≤2r+t+u, 1≤j,n≤2r. 事实上,若φ可以扩充为G的自同构,则〈bjai,bnam〉=G,1≤i,m≤2r+t+u,1≤j,n≤2r,且bjai、bnam满足与a、b相同的定义关系.由引理2,in-jm≡/ 0(mod 2).由o(bnam)=2r知,m必为偶数(若否,则o(bnam)=2r+t+u). 于是由引理6知,m≡0(mod 2t+u),进而(i,2)=(n,2)=1. 由引理4知, (bjai)bnam=bja-m(1+2r+t)j+i(1+2r+t)n+m, (bjai)1+2r=bjai(1+2r+t), 由引理1(i)知G可裂,于是有-m(1+2r+t)j+i(1+2r+t)n+m≡i(1+2r+t)(mod 2r+t+u). 由于m≡0(mod 2t+u),故i(1+2r+t)n≡i(1+2r+t)(mod 2r+t+u),解得n≡1(mod 2u). 反之,若i,j,m,n满足上述关系式,易证〈bjai,bnam〉=G,且bjai、bnam满足与a、b相同的定义关系,从而φ可以扩充为G的自同构,故|Aut(G)|等于满足上述关系式的i,j,m,n的各种可能的取法.因i有2r+s+u-1种取法,j有2r种取法,m有2r种取法,n有2r-u种取法,故|Aut(G)|=24r+t-1. 对于(ii),下证φ可以扩充为G的自同构的充要条件是i,j,m,n满足关系式: i≡j′2s-n-m2t(mod 2u),j≡0(mod 2s+t), n≡1(mod 2s+u),1≤i,m≤2r+s+u, 1≤j,n≤2r+s+t. 事实上,若φ可以扩充为G的自同构,则 〈bjai,bnam〉=G,1≤i,m≤2r+s+u, 1≤j,n≤2r+s+t, 且bjai、bnam满足与a、b相同的定义关系.由引理2知in-jm≡/0(mod 2).由引理4知, (bjai)bnam=bja-m(1+2r)j+i(1+2r)n+m,(bjai)1+2r=bj(1+2r)ai[1+(1+2r)j+…+(1+2r)j2r].由于b2r+s+t=a2s+t,令j(1+2r)=x+k2r+s+t,其中,k∈Ζ,则 于是j≡0(mod 2s+t),从而(i,2)=(n,2)=1.又由引理3知,(1+2r)j≡1(mod 2r+s+t),令(1+2r)j=1+k′2r+s+t,1+(1+2r)j+…+(1+2r)j2r=(1+2r)+l2r+s+t,其中,k′,l∈Ζ,则-mk′2r+s+t+i(1+2r)n≡k2r+s+i(1+2r)+il2r+s+t(mod 2r+s+u),于是n≡1(mod 2s+u).再由(bnam)2r+s+t=(bjai)2r+s得 i≡j′2s-n-m2t)(mod 2u),其中,j=j′2s+t. 反之,若i,j,m,n满足上述关系式,易证〈bjai,bnam〉=G,且bjai、bnam满足与a、b相同的定义关系,从而φ可以扩充为G的自同构. 可见|Aut(G)|等于满足上述关系式的i,j,m,n的各种可能的取法. 因i有2r+s种取法,j有2r种取法,m有2r+t+u种取法,n有2r+t-u种取法,故|Aut(G)|=24r+2s-u. 定理3设G为无循环极大子群的例外亚循环2群,即 G=〈a,b|a2n=1,b2m=a2k,ab=a-1+2l〉, 其中,m,n≥2,k≥n-1,2≤l≤n,m≥n-l. (1) 若k=n,m>n-l,n>l,则|Aut(G)|=2m+n+l; (2) 若k=n,m>n-l,n=l,则|Aut(G)|=2m+n+l-1; (3) 若k=n,m=n-l,则|Aut(G)|=2m+n+l-1; (4) 若k=n-1,m>n-l,n>l+1,则|Aut(G)|=2m+n+l; (5) 若k=n-1,m>n-l,n=l+1,则|Aut(G)|=2m+n+l-1; (6) 若k=n-1,m>n-l,n=l,则|Aut(G)|=2m+n+l-2; (7) 若k=n-1,m=n-l,则|Aut(G)|=2m+n+l-1. 证明 设φ:a→bjai,b→bsar是一映射,下面依次计算它们的自同构群的阶. 对于(1),(2),此时G=〈a,b|a2n=1,b2m=a2k,ab=a-1+2l〉.下证当n>l时,φ∈Aut(G)⟺i,j,r,s满足关系式:(i,2)=1,j≡0(mod 2m-1),s≡1(mod 2n-l),1≤i,r≤2n,1≤j,s≤2m.当n=l时,φ∈Aut(G)⟺i,j,r,s满足关系式:(i,2)=1,j≡0(mod 2m-1), (s,2)=1,1≤i,r≤2n,1≤j,s≤2m. 事实上,若φ∈Aut(G),则〈bjai,bsar〉=G,1≤i,r≤2n,1≤j,s≤2m,且bjai、bsar满足与a、b相同的定义关系.由引理2知is-jr≡/ 0(mod 2).由引理4知,(bjai)bsar=bja-r(-1+2l)j+i(-1+2l)s+r,且(bjai)-1+2l=bj(-1+2l)ai[1+(-1+2l)j+…+(-1+2l)j(2l-2)].由引理1(ii)知G可裂,于是有 故j≡0(mod 2m-1),从而(i,2)=(s,2)=1.又由引理3知,(-1+2l)j≡1(mod 2m+l-1),由于m>n-l,故(-1+2l)j≡1(mod 2n),进而可得i(-1+2l)s≡i(-1+2l)(mod 2n),于是当n>l时,s≡1(mod 2n-l);当n=l时,(s,2)=1. 反之,若i,j,r,s满足上述关系式,易证〈bjai,bsar〉=G,且bjai、bsar满足与a、b相同的定义关系,从而φ∈Aut(G). 可见|Aut(G)|等于满足上述关系式的i,j,r,s的各种可能的取法,即当n>l时,|Aut(G)|=2m+n+l;当n=l时,|Aut(G)|=2m+n+l-1. 对于(3),下证φ∈Aut(G)⟺i,j,r,s满足关系式:(i,2)=1,j≡0(mod 2m-1),r≡0(mod 2)s≡1(mod 2n-l), 1≤i,r≤2n,1≤j,s≤2m. 事实上,若φ∈Aut(G),则〈bjai,bsar〉=G,1≤i,r≤2n,1≤j,s≤2m,且bjai、bsar满足与a、b相同的定义关系.由引理2知is-jr≡/0(mod 2).由引理4知,(bjai)bsar=bja-r(1+2l)j+i(-1+2l)s+r,且(bjai)-1+2l=bj(-1+2l)ai[1+(-1+2l)j+…+(-1+2l)j(2l-2)].由引理1(ii)知G可裂,于是有 故j≡0(mod 2m-1),从而(i,2)=(s,2)=1.又由引理3知,(-1+2l)j≡1(mod 2m+l-1),由于m=n-l,故(-1+2l)j≡1(mod 2n-1).又由o(bsar)=2m知,r必为偶数.于是上式可转化为i(-1+2l)s≡i(-1+2l)+ik2n-1(mod 2n),解得s≡1(mod 2n-l). 反之,若i,j,r,s满足上述关系式,易证〈bjai,bsar〉=G,且bjai、bsar满足与a、b相同的定义关系,从而φ∈Aut(G). 可见|Aut(G)|等于满足上述关系式的i,j,r,s的各种可能的取法,即当m=n-l时,|Aut(G)|=2m+n+l-1. 对于(4),(5),(6),此时G=〈a,b|a2n=1,b2m=a2n-1,ab=a-1+2l〉.下证 当n-1=l时,φ∈Aut(G)⟺i,j,r,s满足关系式: (i,2)=1,j=2m,s≡1(mod 2),1≤i,r≤2n,1≤j,s≤2m. 当n=l时,φ∈Aut(G)⟺i,j,r,s满足关系式: (i,2)=1,j=2m,s≡1(mod 2),1≤i,r≤2n,1≤j,s≤2m. 当n-l>l时,φ∈Aut(G)⟺i,j,r,s满足关系式: (i,2)=1,j≡0(mod 2m-1),s≡1(mod 2n-l) 1≤i,r≤2n,1≤j,s≤2m. 事实上,若φ∈Aut(G),则〈bjai,bsar〉=G,1≤i,r≤2n,1≤j,s≤2m,且bjai、bsar满足与a、b相同的定义关系.由引理2知is-jr≡/ 0(mod 2).由引理4知,(bjai)bsar=bja-r(-1+2l)j+i(-1+2l)s+r,且(bjai)-1+2l=bj(-1+2l)ai[1+(-1+2l)j+…+(-1+2l)j(2l-2)].由于b2m=a2n-1,令j(-1+2l)=x+k2m,其中,k∈Ζ,则 于是j≡0(mod 2m-1),从而(i,2)=(s,2)=1.又(-1+2l)j≡1(mod 2m+l-1),由于m>n-l,故(-1+2l)j≡1(mod 2n),进而i(-1+2l)s≡i(-1+2l)+ik2n-1(mod 2n),于是有 又当s≡1(mod 2)时,可得k为偶数,进而j=2m. 反之,若i,j,r,s满足上述关系式,易证〈bjai,bsar〉=G,且bjai、bsar满足与a、b相同的定义关系,从而φ∈Aut(G).故 对于(7),下证φ∈Aut(G)⟺i,j,r,s满足关系式: (i,2)=1,j≡0(mod 2m-1),r≡0(mod 2),s≡1(mod 2n-l), 1≤i,r≤2n,1≤j,s≤2m. 事实上,若φ∈Aut(G),则〈bjai,bsar〉=G,1≤i,r≤2n,1≤j,s≤2m,且bjai、bsar满足与a、b相同的定义关系.由引理2知is-jr≡/ 0(mod 2). 由引理4知,(bjai)bsar=bja-r(-1+2l)j+i(-1+2l)s+r,且(bjai)-1+2l=bj(-1+2l)ai[1+(-1+2l)j+…+(-1+2l)j(2l-2)].由于b2m=a2n-1,令j(-1+2l)=x+k2m,其中,k∈Ζ,则 于是j≡0(mod 2m-1),从而(i,2)=(s,2)=1.又由 (bsar)2m=(bjai)2n-1知,r必为偶数.于是i(-1+2l)s≡k2n-1+i(-1+2l)+ik′2n-1(mod 2n),其中,k′∈Ζ,解得s≡1(mod 2n-l). 反之,若i,j,r,s满足上述关系式,易证〈bjai,bsar〉=G,且bjai、bsar满足与a、b相同的定义关系,从而φ∈Aut(G).故|Aut(G)|等于满足上述关系式的i,j,r,s的各种可能的取法,即当m=n-l时,|Aut(G)|=2m+n+l-1. 综上可知,亚循环2群的自同构群的阶已计算完毕,比较群G的阶与自同构群的Aut(G)的阶可知|G|||Aut(G)|,因此有下面的定理4. 定理4设群G是亚循环2群,则群G满足LA猜想. [1] 徐行忠. 换位子群为p阶子群的有限p-群的自同构[D].武汉:湖北大学, 2008. [2] 余曙霞. 若干非交换p-群的自同构群的阶[J].广西大学学报(自然科学版), 1982, 1:89-93. [3] 邵明文.p5阶群的自同构群的阶(Φ1-Φ5)[D].南宁:广西大学, 2002. [4] 蓝永红.p5阶群的自同构群的阶(Φ6-Φ10)[D].南宁:广西大学, 2002. [5] 班桂宁, 张 玉, 吴建平, 等. 基于p5阶Φ2族群的LA群[J].广西师范学院学报(自然科学版), 2008, 25(3):1-4. [6] 王 勇, 班桂宁. 计算有限p-群的自同构群阶的方法[J].江西师范大学学报(自然科学版), 2002, 33(1):12-16. [7] 班桂宁, 张新政, 王 勇.p-群的自同构群的阶[J].西南师范大学学报(自然科学版), 2005, 30(4):600-603. [8] 李延波.p6阶群Φ14,Φ15,Φ22的自同构群的阶[D]. 南宁:广西大学, 2004. [9] 董心灵.p6阶群的自同构群的阶[D]. 南宁:广西大学, 2004. [10] 何常香.p6阶群(Φ14,Φ15,Φ22)的自同构群的阶[D]. 南宁:广西大学, 2004. [11] BIRKOFF G, HALL P. On the order of groups of automorphisms[J]. Trans Amer Math Soc, 1936, 39: 489-499. [12] DAVITT R M. The automorphism groupsof finite matacyclic p-groups[J]. Proc Ame Math Soc, 1970, 25:876-879. [13] XU M Y, ZHANG Q H. A claaaification of matacyclic 2-groups[J]. Algebra Colloq, 2006, 13(1):25-34. [14] 陈 蓉. 亚循环的内交换p-群的自同构群[D]. 临汾:山西师范大学, 2007. [15] 徐明耀, 曲海鹏. 有限p-群[M]. 北京:北京大学出版社, 2010. The LA-conjecture of metacyclic 2-groups BAI Jie, ZHANG Huiling (Department of Mathematics, Taiyuan University, Taiyuan 030001) LA-conjecture is famous in finitep-groups. In this paper, according to the classification of metacyclic 2-groups, the orders of automorphism groups of metacyclic 2-groups are calculated including the ordinary and exceptional metacyclic 2-group of cyclic and non-cyclic maximal subgroup. Moreover, the LA-conjecture is proved to be true for metacyclic 2-groups. p-group; metacyclic 2-groups; automorphism group; order; LA-conjecture 2015-03-18. 国家自然科学青年基金项目(11101251). 1000-1190(2015)06-0822-05 O152 A *E-mail: baijiemao@163.com.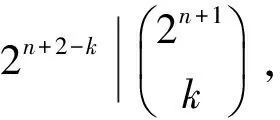

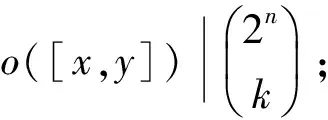
2 亚循环2群的自同构群阶
