基于粒子群优化算法的微电网微电源优化配置

2015-03-22王新永闫立东

现代建筑电气 2015年3期

关键词：储能风速粒子

王新永, 闫立东

(国家电网枣庄供电公司,山东枣庄 277000)

基于粒子群优化算法的微电网微电源优化配置

王新永, 闫立东

(国家电网枣庄供电公司,山东枣庄 277000)

提出一种基于粒子群优化算法的微电网微电源优化配置模型,并以权重系数法对其进行研究,得出在各个权重系数情况下各类微电源的最佳运行容量。以孤岛微电网系统为例,考虑了各类微电源的出力及它们之间的互补特性和微电网系统内各种负荷的不同敏感性。通过运用粒子群优化算法加以求解。仿真结果表明,优化配置方法可以满足负荷多样性需求情况下的微电网经济运行,可为微电网系统优化规划问题提供一定的参考。

微电网; 粒子群优化算法; 孤岛; 优化配置

0 引言

近年来,微电网技术作为一个较为前沿的研究学科,以其对可再生能源利用的高可靠性、多样性、交互性、独立性等特点[1-2],在欧美国家得到了大力发展,在我国也将其作为智能电网研究的重要组成部分在863、973等国家重点研究发展规划中进行了立项研究,并通过示范性工程对相关的理论及技术成果进行验证[3]。随着微电网技术的日趋成熟以及可再生能源发电成本的不断下降,对微电网的实际应用已迫在眉睫,因此对于微电网规划问题研究已尤为重要。

在微电网规划问题中,分布式电源的选型、选址定容问题是一个重要和复杂的问题[4-5]。目前,国内外学者对其进行了相关的研究,并取得了一些理论与实践方面的成果。文献[6]通过运用缺电概率技术对微电网分布式电源进行优化配置。文献[7-8]在考虑经济性、可靠性和环保性基础上,建立了将分布式发电作为备用电源的电源容量优化配置模型。文献[9]考虑风能、太阳能的随机性和波动性给分布式电源优化配置带来的影响,并采用改进细菌觅食算法对微电网电源进行优化配置。现有规划目标中从投资、损耗、可再生能源利用等这些角度出发,还没有更好地兼顾用户的利益。随着未来电力市场竞价机制的逐渐成熟,尤其需要这方面的研究成果。

本文从权衡用户侧与发电侧双边的利益角度出发,基于粒子群优化(Breeding Particle Swarm Optimization,BPSO)算法提出了微电网微电源优化目标函数,并考虑微电源的出力及波动互补性、供电可靠性等约束条件,建立了基于改进粒子群算法对该问题进行求解的优化方案,并以孤岛微电网系统为例进行了仿真。

1 微电网系统中各个组成部分的数学模型

以含有风力发电、光伏发电、储能系统的孤岛微电网的系统进行研究,并假设各电力电子装置能完全转换且能完成即插即用功能且效率为100%。微电网系统框图如图1所示。

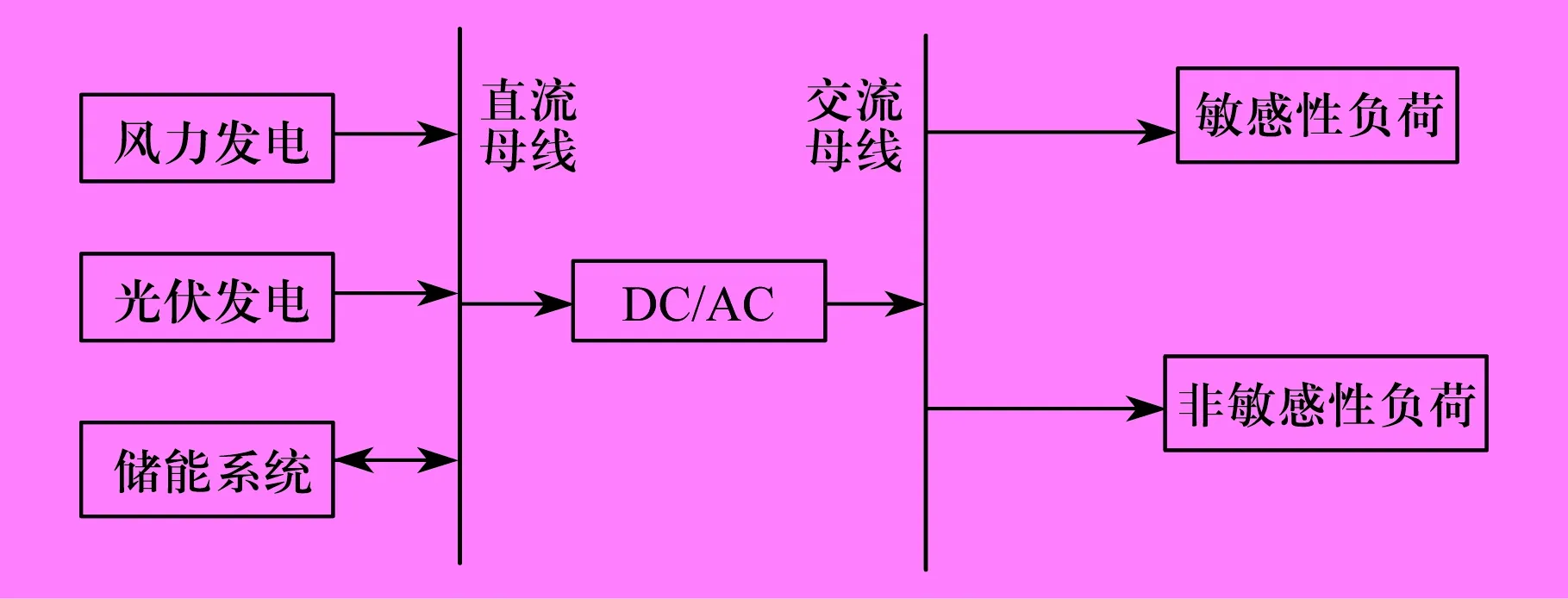
图1 微电网系统框图

1.1 光伏发电模型

光伏列阵实际输出功率[10]为

Ppv(t)=ηgNpvAmG(t)

(1)

式中:ηg——瞬时光伏阵列发电效率;

Am——光伏电池接受光照的的面积;

G(t)——地球在单位面积的关照强度;

Npv——光伏阵列含有光伏电池数目。

假设光伏发电的并网损耗、线路损耗和其他的所有损耗为0,则瞬时光伏阵列发电效率为

ηg=ηrηpt[1-βt(TC-Tr)]

(2)

式中:ηr——光伏发电参考效率;

ηpt——追踪设备的功率效率,可取1;TC——光伏电池温度;

βt——硅电池功率温度系数,取0.004～0.006 ℃;

Tr——光伏电池参考温度。

多数情况下,环境温度与光伏电池的温度是不相同的,两者的换算关系[11]为

TC=Ta+βGt

(3)

式中:Ta——环境温度;

β——系数,通常取值为0.03 km2/W。

1.2 风力发电模型

风力电机的功率输出特性可以看成中心高度。

风速的分段函数,数学模型如下[12]:

PW(t)=

(4)

式中:vct——风力机的切入风速;

v(t)——风力机的实际风速;

vr——风力机的额定风速;

vco——风力机的切出风速;

Pr——单台风力机组的额定输出功率;PW(t)——实际输出功率。

风速v可以通过参考点的风速转换出:

(5)

式中:v——中心高度H的风速;

vr——参考高度Hr的风速;

α——指数,一般取0.14。

实际风力发电系统中,可利用的输出功率为

PWG(t)=PW(t)AWηNWG

(6)

式中:AW——风流过的面积;

η——转换效率;

NWG——风力系统风力机的台数。

1.3 储能系统模型

储能系统的可用容量与上一时刻的当前功率需求关系有关,可表示[13]如下:

Ebat(t+Δt)=Ebat(t)+[PWG(t)+PPV(t)-

PL(t)/ηc]Δtηcf

(7)

式中:ηc——逆变转换效率;

ηcf——储能系统充放电效率。

在任何情况下,储能系统都要受到下列不等式的约束:

Ebatmin≤Ebat(t)≤Ebatmax

(8)

Ebatmin=(1-γ)Ebatmax

式中:Ebatmin——最小可用存储容量;

Ebatmax——最大可用存储容量;

γ——充放电深度,取0.8。

1.4 负荷模型

考虑所有因素的时序负荷模型在实际运算中难以实现,故采用短期负荷与长期最大负荷的比值来表示仿真时刻负荷的期望值,利用服从正太分布的负荷波动来模拟不确定因素对负荷的影响。年负荷的期望值为

L(t)=ηw(t)ηd(t)ηh(t)PLmax+N(0,σ2)

(9)

式中:ηd(t)——天负荷占年负荷峰值的百分比;

ηh(t)——小时负荷与年负荷峰值的百分比;

ηw(t)——周负荷峰值占年负荷峰值的百分比。

本文采用的峰值负荷为500 kW。年负荷曲线如图2所示。

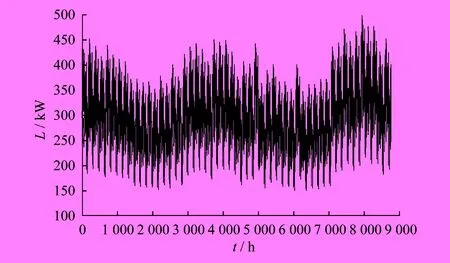
图2 年负荷曲线

2 微电网微电源优化配置数学模型

2.1 优化配置目标函数

2.1.1 发电侧目标函数

对于发电方来说,主要考虑降低投资费用,故目标函数内容为投资费用、运行费用、维护费用、燃料费用[11]。考察的重点是可再生能源,故对于燃料费用不再考虑。直接运用已有数据,故其目标函数为

(10)

式中:N——电源的类型数目;

xi——第i种电源的数目;

CCBi——第i种电源的等年值的设备购买费用;

CSCi——第i种电源安装费用;

COMi——第i种电源的年运行和维护费用。

2.1.2 负荷侧目标函数

对于负荷侧来说,用户考虑的是负荷的丢失对其经济和精神损失最小,对于有的部分很难用特定的数学进行量化,只能对实际的负荷区域进行统计,求其损失期望值。微电网负荷可以分为可间断负荷和不可间断负荷,可将其目标函数表示为

(11)

Li(t)=

(12)

式中:LElost——负荷的期望停电损失;

Li(t)——i时间段内的停电损失;

PI(t)——i时间段内可间断的负荷;

αI——可间断负荷损失系数;

αU——不可间断负荷损失系数;

PT(t)——i时间段丢失的负荷。

计算方法如下

(13)

式中:PS(t)——系统可用输出功率;

PL((t)——系统所需负荷功率。

2.1.3 整体优化目标函数

对于存在一部分互相矛盾的两个优化目标,采用常见的多目标优化处理办法,运用权重系数法建立目标函数对其行研究,得出整体目标函数为

MinF=ω1CCF(x)+ω2LElost

(14)

ω1+ω2=1

式中:ω1、ω2——相应部分的权重系数。

2.2 优化配置约束条件

2.2.1 系统能量守恒约束

系统能量守恒约束条件:

PPV+PWG+PBD+PUN=PL+PBC+PEG

(14)

式中:PBD——储能放电量;

PUN——未被释放的能量;

PBC——储能充电量;

PEG——过发的电量。

2.2.2 微电源出力约束

对于第i种电源[15],有

Pi≤pixi

(15)

式中：Pi——单机容量;

pi——单机容量。

2.2.3 储能系统约束

对于储能系统,除了要满足式(8)外还要满足[15]

(16)

式中:P+、P-——每小时内的充放电。

2.2.4 可靠性约束

缺电概率(Loss of Power Supply Probability,LPSP)为全年孤岛运行的微电网可靠性指标,不大于系统最大允许缺电概率LPSPmax。本文LPSPmax取0.4%。

3 BPSO算法

BPSO算法步骤[16-18]如下:

(1) 随机初始化种群中各粒子的位置和速度。

(2) 评价每个粒子的适应度值,并储存当前粒子的位置和适应度值到每个粒子的pbest,将所有pbest中适应度值最优个体的位置和适应度值储存于gbest中。

(3) 更新每个粒子的速度和位置。

(4) 将每个粒子适应度值与前期经历的最好位置作比较,如较好,将其作为当前位置。

(5) 比较当前所有pbest、gbest的值，更新gbest。

(6) 根据杂交概率,选取指定数量的粒子放入杂交池内,池中的粒子随机两两杂交产生同样的子代粒子。

(7) 若满足停止条件,搜索停止,输出结果,否则回到第(3)步继续搜索。

优化配置流程图如图3所示。

图3 优化配置流程图

4 算例分析

本文以孤岛微电网系统为例,微电源参数[7,9,18]如下:蓄电池效率为90%,放电率在25 ℃情况下每月为1%,额定电压为12 V,最小充电20%初始容量为1 kWh,使用寿命为4 a。光伏发电,额定电压为17.6 V,额定电流为7.1 A,开路电压为22.1 V,短路电流为7.54 A,参考温度为25 ℃,使用寿命20 a,一个光伏电池的面积为1.108 m2。风力发电切入风速为2.5 m/s,额定风速为12 m/s,切出风速为25 m/s,使用寿命为20 a。年风速曲线如图4所示。统计数据,年光照曲线如图5所示。微电源经济参数如表1所示。

图4 年风速曲线

系统仿真配置结果如表2所示。

表2中,δ为敏感性负荷所占负荷比重,ω1、

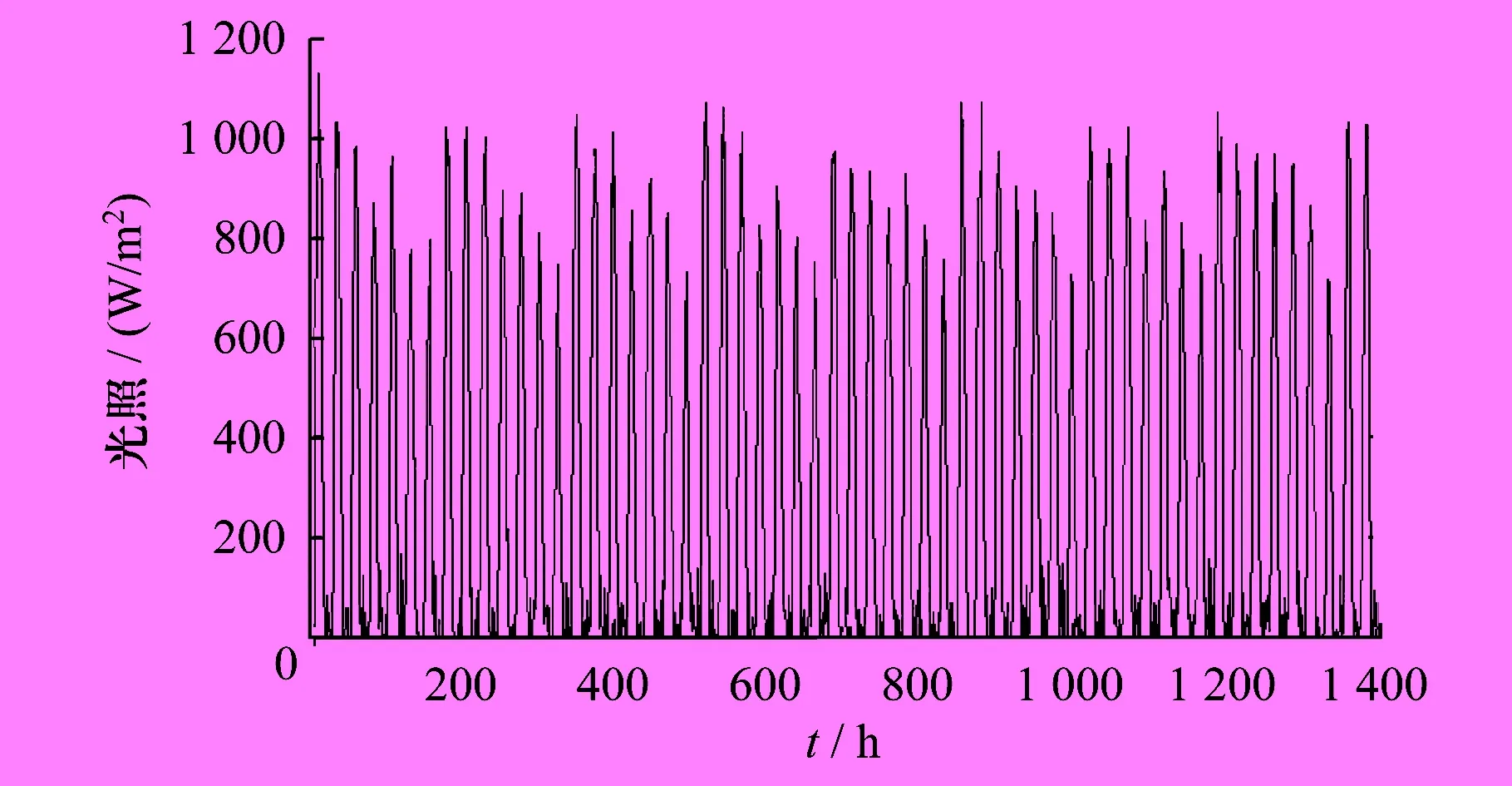
图5 年光照曲线

ω2分别为双边目标权重值,Npv、Nwg、Nbat分别为光伏电池、风力机、储能电池配置数目。

由分析结果可知,随着不可间断负荷比重的增加,负荷侧的目标函数对优化配置结果的影响甚为明显,故当可间断负荷比重较大时,对于负荷侧的考虑尤为必要,但敏感性负荷比重较小时,负荷侧对优化效果影响较小,可适当降低其权重或不考虑。

表1 微电源经济参数

表2 系统仿真配置结果

5 结语

提出更适应未来竞争性电力市场的微电网电源优化配置问题方案,即考虑发电侧和用户侧利益的优化模型。运用改进的粒子群算法,对满足一定供电可靠性的孤岛微电网系统进行了仿真研究。仿真得到相应的微电网电源装机容量最优配置方案,验证了优化算法的可行性,为双边目标函数权重的取值提供了方向性的参考。

[1] 鲁宗相,王彩霞,闵勇,等.微电网研究综述[J].电力系统自动化,2007,31(19):1002107.

[2] 肖宏飞,刘士荣,郑凌蔚,等.微型电网技术研究初探[J].电力系统保护与控制,2009,37(8):115-119.

[3] LASSETER J,ETO H,SCHENKMAN B,et al.BCERTS micro-grid laboratory test bed[J].IEEE Transactions on Power Delivery,2011,26:325.

[4] 罗运虎,王冰洁,梁昕,等.电力市场环境下微电网不可再生分布式发电容量的优化配置问题[J].电力自动化设备,2010,30(8):28-33.

[5] 张勇,吴淳.分布式发电机在配电网中的优化配置[J].电力系统保护与控制,2010,38(11):33-37.

[6] MOGHADDAS-TAFRESHI S M,ZAMANI H A,HAKIMI S M.Optimal sizing of distributed resources in a micro grid with loss of power supply probability technology by using breeding particle swarm optimization[J].Renewable Sustainable Energy,2011:043105.

[7] 王瑞琪,李珂,张承慧.基于混沌多目标遗传算法的微网系统容量优化[J].电力系统保护与控制,2011,39(22).

[8] 郑漳华,艾芊,顾承红,等.考虑环境因素的分布式发电多目标优化配置[J].中国电机工程学报,2009,29(13):23-28.

[9] 马溪原,吴耀文,方华亮,等.采用改进细菌觅食算法的风/光/储混合微电网电源优化配置[J].中国电机工程学报,2011,31(9):17-25.

[10] GAVANIDOU E,BAKIRTZIS A.Design of a stand alone system with renewable energy sources using trade off methods[J].IEEE Transaction on Energy Conversion,1992,7(1):42-48.

[11] HASSANZADEHFARD H,MOGHADDAS-TAFRE-SHI S M,HAKIMI S M.Optimal sizing of grid connected micro-grid using particle swarm optimization considering interruptible loads[J].Electrimacs,2011,4(3):1216-1221.

[12] MOGHADDAM A A,SEIFI A,NIKNAM T,et al.Multi-objective operation management of a renewable MG(micro-grid) with back-up micro-turbine/fuel cell/battery hybrid power source[J].Fuel and Energy,2011,36(11):6490-6507.

[13] HASSANZADEHFARD H,MOGHADDAS-TAFRE-SHI S M,HAKIMI S M.Effect of energy storage systems on optimal sizing of islanded micro-grid considering inter-ruptible loads,energetics(IYCE)[C].Proceedings of the 3rd International Youth Conference,2011.

[14] MORAIS H,KáDáR P,FARIA P,et al.Optimal scheduling of a renewable micro-grid in an isolated load area using mixed-integer linear programming[J].Renew Energy,2010(35):151-156.

[15] HAKIMI S M,MOGHADDAS-TAFRESHI S M.Unit sizing of a stand-alone hybrid power system using particle swarm optimization(PSO)[J].IEEE ICAL,2007(18-21):3107-3112.

[16] 龚纯,王正林.精通MATLAB优化计算[M].2版.北京:电子工业出版社,2012.

[17] 李明.详解MATLAB在最优化计算中的的应用[M].北京:电子工业出版社,2011.

[18] 杨毅,韦钢,周冰,等.含分布式电源的配电网模糊优化规划[J].电力系统自动化,2010,34(13):19-23.

【办刊理念】

以促进创新与发展为己任

以满足读者需要为追求

以创办一流期刊为目标

专业权威可靠引导趋势发行渠道优越覆盖面广

应用深入实践贴近市场服务专业细致客户至上

Optimal Allocation of Micro Power Sources in Micro Grid Based on Breeding Particle Swarm Optimization Algorithm

WANG Xinyong, YAN Lidong

(Zaozhuang Power Supply Company of State Grid, Zaozhuang 277000, China)

Based on breeding particle swarm optimization(BPSO),this paper proposed an optimal allocation model of micro power sources in micro grid,taking the benefit of both the generation side and the user side.The model was studies by the weight coefficient method.The optimal capacity of various types of micro power sources were obtained under different weight coefficient cases.As an example of the isolated island micro grid,the output characteristics and complementary characteristics of various types of micro-power and the load different sensitivity within the micro grid system were considered.This paper used BPSO algorithm for solving the minimization problem.The simulation results show that the methodology can meet economic operation of micro-power system with diversity load.This method can provide

for the planning and optimization problem of micro grid.

micro grid; breeding particle swarm optimization(BPSO) algorithm; isolated island; optimal allocation