线缆热稳定性的量化分析
2015-03-22陶卫列
陶 卫 列
(四川山鼎建筑工程设计股份有限公司, 四川 成都 610021)
线缆热稳定性的量化分析
陶 卫 列
(四川山鼎建筑工程设计股份有限公司, 四川 成都 610021)
基于JGJ 16—2008《民用建筑电气设计规范》,导出了适用范围更广的热稳定性校验公式,量化分析了线缆热稳定问题,获得了一些重要数据,在实际案例中得到了应用。指出单、双相短路时,线缆一般均能满足热稳定要求,可不做校验。
热稳定性; 量化分析; 热效应; 极限短路点
0 引 言
在配电系统的运行过程中,有时会发现某些低压电缆未用多长时间就发生了内部短路。由于准确查找内部短路点比较困难,通常会重设其他电缆而舍去此电缆,造成了原电缆的报废。其实,发生此问题的一个重要原因,也许就是线缆的热稳定性未达到要求。在某次短路时,线缆超过了极限允许温度,绝缘性能受到了一定程度的损伤,使用寿命缩短,为电缆的运行埋下了隐患。因此,线缆的热稳定性极其重要,它直接关系到系统运行的安全性和可靠性。短路点离电源越远,短路电流越小,其热效应越低。所以,必然存在极限短路点,其短路电流热效应刚好等于线缆允许的热效应。
本文对线缆热稳定性进行量化分析。
1 计算公式
计算前提条件是短路点远离发电机。
JGJ 16—2008《民用建筑电气设计规范》第7.6.3条规定,当短路持续时间不大于5 s时,绝缘导体的热稳定应按下式进行校验:
(1)
式中:S——绝缘导体的线芯截面;
I——短路电流有效值(方均根值);
t——在已达到正常运行时的最高允许温度的导体上升至极限温度的时间;
K——不同绝缘、不同线芯材料的热稳定系数。
当短路持续时间小于0.1 s时,应计入短路电流非周期分量的影响;当短路持续时间大于5 s时,应计入散热影响。
利用式(1)可进行量化分析,但它有一定的适用范围。为解决该问题,需要对式(1)进行变换和调整。
由式(1),得
S2K2≥I2t
(2)
如考虑非周期分量的影响,可用i代替I,则有
(3)
i=Imsin(ωt+α-φk)+Ae-t/Ta
A=Im1sin(α-φ)-Imsin(α-φk)
式中:i——全短路电流瞬时值;
Im——全短路电流周期分量幅值;
Im1——正常负荷电流幅值;
α——短路初相角;
φ——负荷功率因数角;
φk——短路阻抗角;
Ta——L/r时间常数;
ω——角速度。
由此,由式(3)得
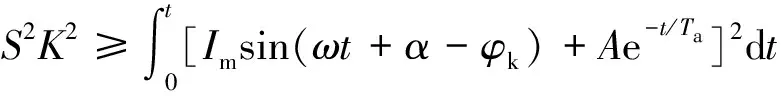
(4)
求解式(4),得
S2K2≥U(t)+V(t)+W(t)+C
(5)
其中:
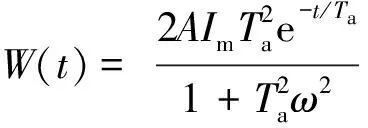
sin(α-φk)cosωt]+ω[sin(α-φk)·
sinωt-cos(α-φk)cosωt]}
积分常数C可通过边界条件t=0,热效应值为0时求得。导出全短路电流有效值为
(6)
可得
式(5)考虑了短路电流非周期分量的影响,适用于短路发生至5 s内的任何时刻。由于塑壳断路器的瞬时动作时间在0.03 s左右,短延时动作时间一般在0.1~1 s,因此短路被切断的时间不会超过5 s。在这段时间内,线缆热稳定性校验均可以通过式(5)来完成。式(5)左边为线缆允许热效应,右边为短路电流热效应。
某参数条件下,热效应、短路电流随时间变化曲线如图1、图2所示。 分析可知,当供电系统各硬件参数、线缆正常负荷、短路点及短路延续时间确定时,其短路电流、负荷电流及功率因数、短路阻抗角、时间常数等都将成为定值,热效应变为初相角α的函数。热效应随α变化的曲线如图3所示。
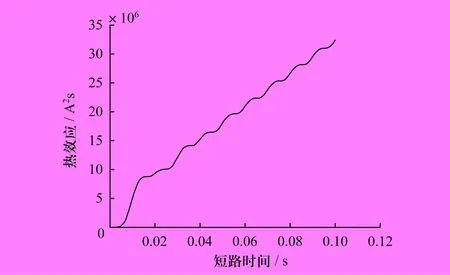
图1 热效应随时间变化曲线
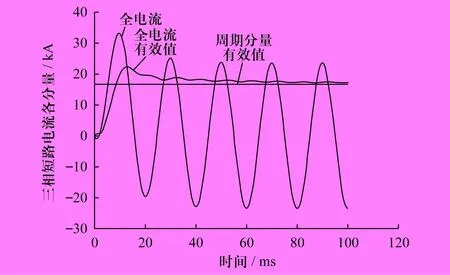
图2 短路电流随时间变化的曲线
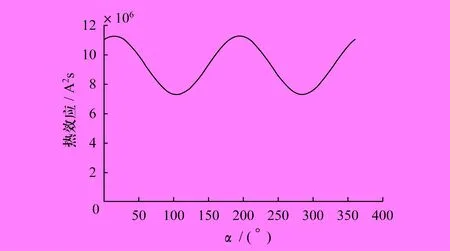
图3 热效应随α变化的曲线
对每一短路点,由于初相角的不同,都存在最大热效应值。热稳定性校验时,应求出该值。通过公式无法一步求出最大值,必须通过双重迭代运算,即从小到大,通过反复给定不同的短路点,并针对每一点给定不同的初相角来计算短路电流热效应值,其结果与线缆允许热效应值相比较,直至求出极限短路点数据。该运算量非常大,可通过计算机编程完成。
2 结果数据
参数条件:系统短路容量为300 MVA;SCB9、SCB10型变压器;TMY-T2(3+2)型母排长度为15 m,实际温度为40 ℃;YJV电缆实际运行温度为80 ℃;电缆正常运行电流以其开关整定值除以1.1确定,功率因数为0.8;迭代运算步长为1 m和1°,其极限短路点最大误差为1 m,即偏大、偏保守,因此可满足工程需要。
按上述条件,随变压器容量、电缆截面、短路持续时间的不同,三相短路时电缆极限短路点数据如表1。

表1 三相短路时电缆极限短路点数据 m
按上述条件,随变压器容量、电缆截面、短路持续时间的不同,单相短路时线缆极限短路点数据如表2所示。
3 实例分析
A点三相短路时两级配电系统图如图4所示。下面来校验电缆热稳定性是否满足要求。
由图4中参数并查表1可知,极限短路点在13 m处,而A点数值小于13 m,因此短路时热稳定性不满足要求。
其他参数不变,仅把图4中的电缆换成YJV-3×35+1×25,再校验电缆热稳定性是否满足要求。
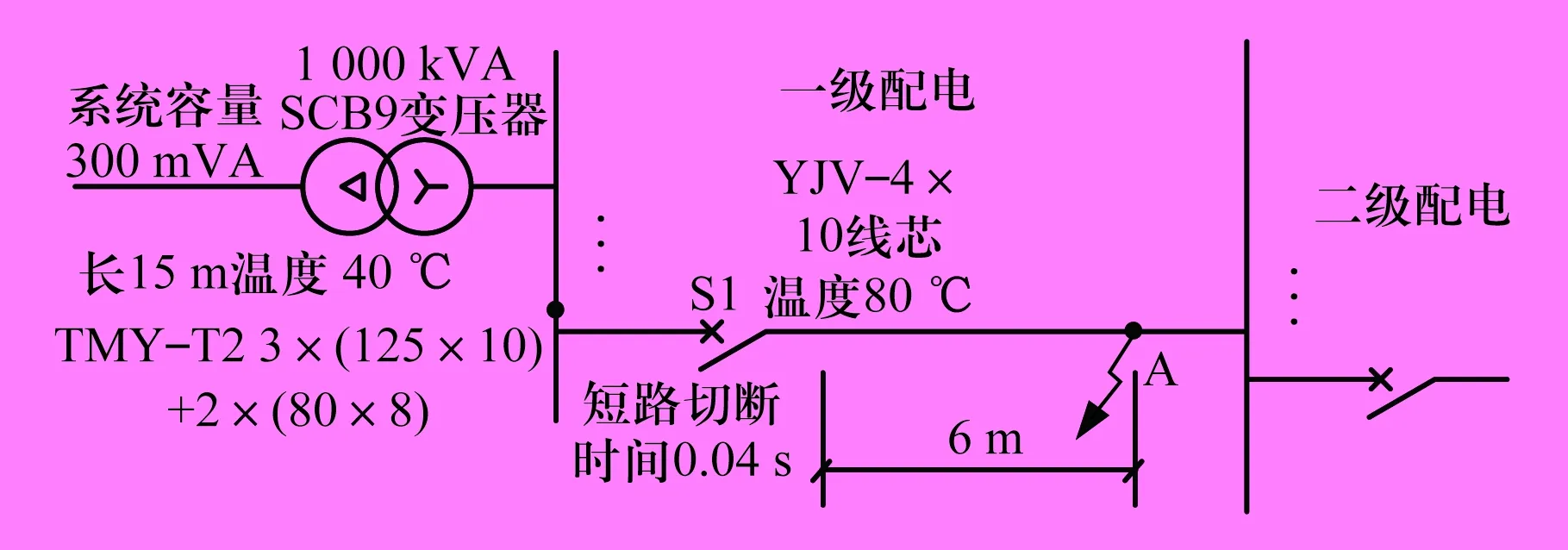
图4 A点三相短路时两级配电系统图
由图4中参数并查表1可知,极限短路点数值为0,由于任何短路点数值均大于0,因此热稳定性满足要求。
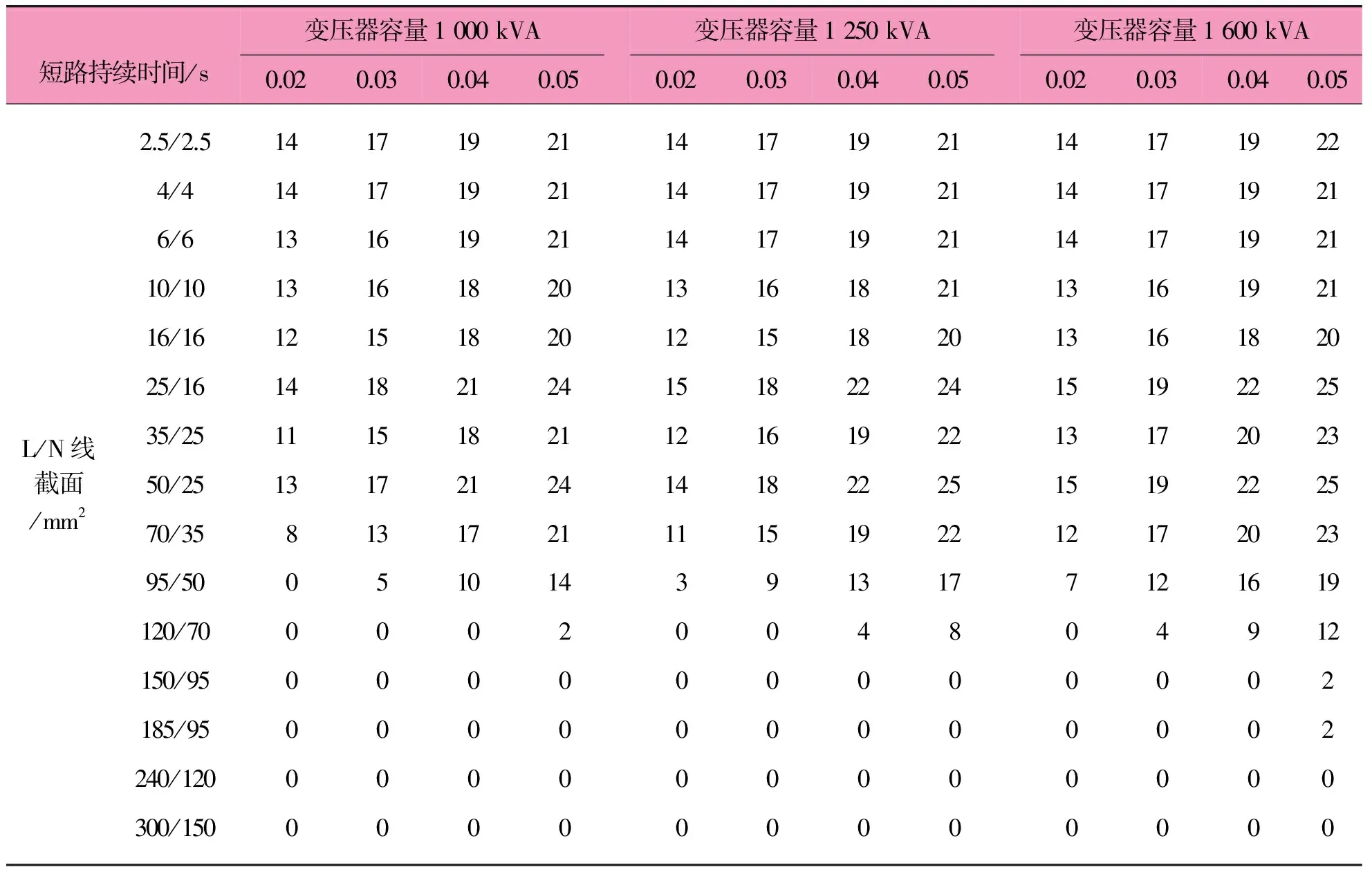
表2 单相短路时线缆极限短路点数据 m
A点单相短路时两级配电系统图如图5所示。下面来校验电缆热稳定性是否满足要求。
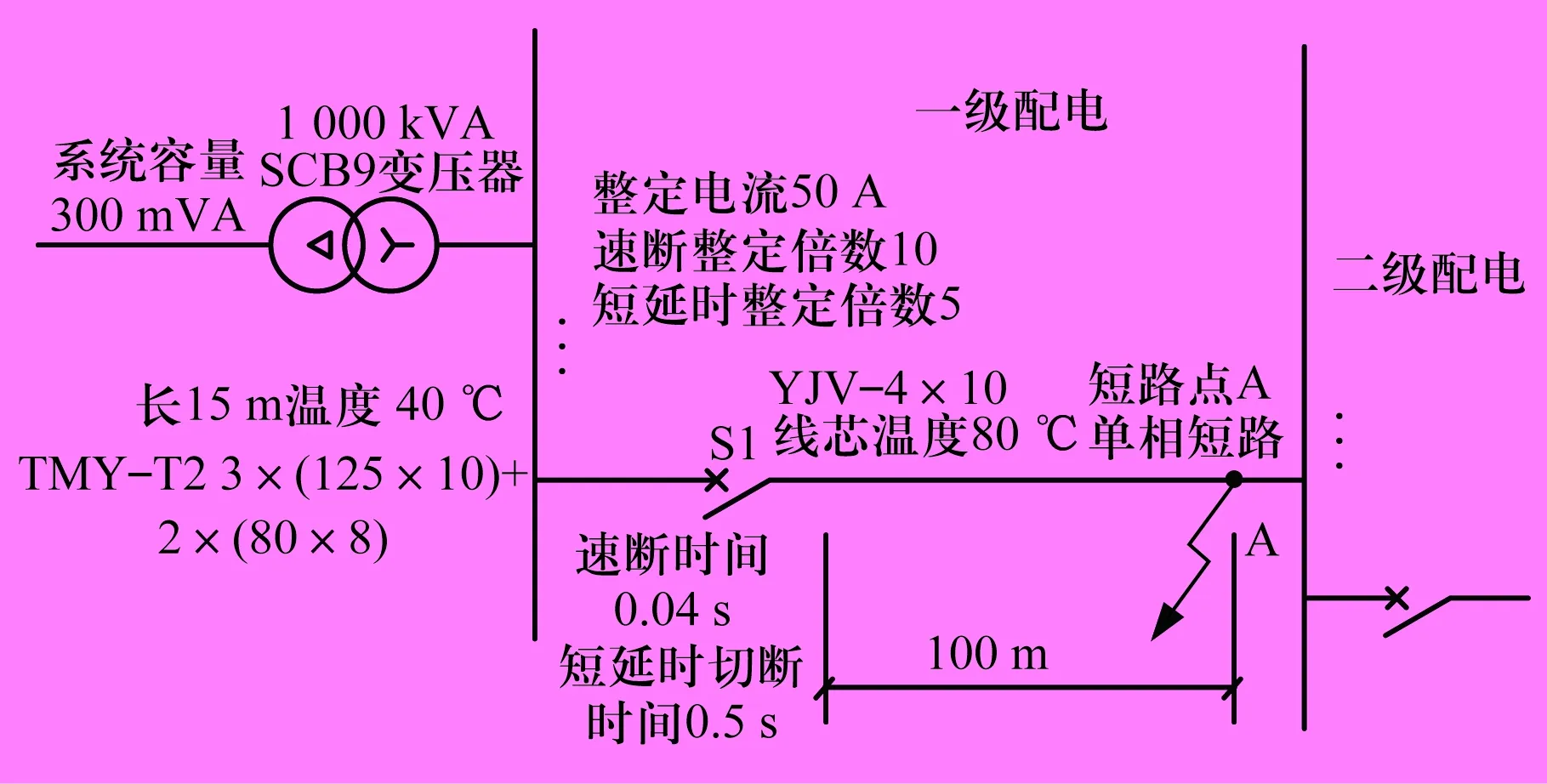
图5 A点单相短路时两级配电系统图
由图5中的参数可计算得出,影响瞬时脱扣器灵敏度的极限短路点在63.7 m,即如果短路点数值大于63.7 m,瞬时脱扣器不能可靠跳闸。因此,应按短延时脱扣时间进行热稳定性校验。
由图5中参数并查表2可知,影响热效应的极限短路点在20 m,由于A点数值为100 m,因此A点单相短路时,热稳定性可满足要求。其实,单相短路时,影响瞬时脱扣器灵敏度的极限短路点数值只要大于热效应的极限短路点数值,热稳定性均可满足要求。
4 结 语
通过以上分析可知:
(1) 短路电流越大,线缆的热稳定性越不易满足要求。一般一级线缆的短路电流远大于二、三级线缆,所以只需校验一级线缆的情况。
(2) 线缆热稳定性与开关的动作时间有很大关系,动作时间越长,越不易满足。所以,当热稳定不满足要求时,可以选用动作时间更短的熔断器来保护线缆。当选用熔断器作线缆保护元件时,一般均可满足要求,无需校验。
(3) 系统短路容量为200~400 MVA时,线缆负荷电流、功率因数的变化对电缆极限断路点的数据影响甚微,可忽略不计。
(4) 单、双相短路且短延时整定时间不超过1 s时,影响瞬时脱扣器灵敏度的极限短路点数值一般均大于热效应的极限短路点数值。所以,线缆热稳定性均能满足要求,可不做校验。但需在开关瞬时、短延时脱扣器整定值正确及可正常动作的前提条件下。
(5) 如果以线缆首端外的第一接线点为短路点,要保证线缆热稳定性满足要求,该点的位置应大于极限短路点数值。

[1] JGJ 16—2008 民用建筑电气设计规范[S].
[2] 耿毅.冶金工业供电[M].北京:冶金工业出版社,1979.
[3] 同济大学数学系.高等数学 上册[M].6版.北京:高等教育出版社,2007.
[4] 中国航空工业规划设计研究院.工业与民用配电设计手册[M].3版.北京:中国电力出版社,2005.
[5] 陶卫列.塑壳断路器整定电流的量化分析[J].现代建筑电气,2014(5):16-21.
[6] GBT 13539—2008 低压熔断器[S].
2015《现代建筑电气》杂志征订单
邮局汇款 银行汇款
邮 编:200063 收款单位:上海电器科学研究院
地 址:上海武宁路505号3号楼4楼 开户银行:招商银行上海分行曹家渡支行
单 位:《现代建筑电气》编辑部 账 号:1219 0973 3310 301
联系电话:021-62574990-272(俞小姐) 传 真:021-62576377
Quantitative Analysis of Cable Thermal Stability
TAO Weilie
(Sichuan Cendes Building Engineering Design Co., Ltd., Chengdu 610021, China)
Based on standard JGJ 16—2008,the thermal stability calibration formula which has a wider application was deduced.Using this formula,the thermal stability of the cable was quantitatively analyzed,and some important data which were used for actual cases were obtained.It is pointed out that the cable usually can meet the requirement of thermal stability at single,dual phase short circuit,so it need not to check the thermal stability.
thermal stability; quantitative analysis; thermal effect; ultimate short-circuit point

《现代建筑电气》杂志订单(回执) 120元/年

陶卫列(1963—),男,高级工程师,从事建筑电气设计。
TM 246
A
1674-8417(2015)03-0007-05
2014-10-24
