高位大跨悬挑结构的抗震分析

李嘉阳 陈世鸣

(同济大学结构工程与防灾研究所，上海200092)

1 引言

动力时程分析是目前预测结构地震响应最准确的手段，但耗费时间和资源较多，且结构在不同地震波下的响应可能差异较大;静力弹塑性分析简便易操作，相对动力时程分析来说结果稳定，且耗费资源较少，该方法已被美国的 ATC－40、FEMA273、FEM274正式采用。某在建艺术文化中心是国内罕见的大跨度高位悬挑混凝土结构，悬挑跨度达15 m，悬挑底层距地面39 m，属于抗震超限结构。本文以其为原型，提取并建立了高位大悬挑结构的力学模型，分析了其抗震性能，研究并讨论了采用静力弹塑性分析方法计算该类大悬挑结构结构响应的准确性。

2 静力弹塑性抗震分析手段

静力弹塑性分析主要基于力的推覆分析、基于位移的推覆分析和MPA法。传统的基于力控制的Pushover分析是采用逐渐增大的呈一定分布规律的侧向荷载来模拟在结构地震作用下各层惯性力的分布［1］，常见的侧向荷载分布模式有以下几种。

1)考虑多个振型的加载模式

首先对结构进行反应谱分析，根据振型分析反应谱平方和开平方(SRSS法)的方法计算结构各层层剪力，再反算各层的水平荷载。其数学表达式为式中，αj表示第j阶振型的质量参与系数;γj表示第j阶振型组合系数;Xij为j振型i质点的水平相对位移;Qij表示第i阶振型第j层的水平力;Qi为第i层振型组合后的水平力;Pi为第i层的层剪力;n为结构总层数;Wi为结构中第i层的重力荷载代表值。

2)倒三角分布模式

侧向荷载沿结构高度的分布与楼层质量和高度成正比的分布模式称为倒三角分布模式。这种加载模式被广泛应用于各国规范，其侧向荷载的数学表达式为

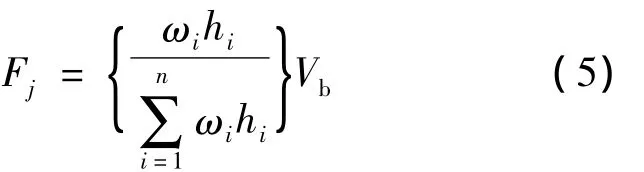
式中，hi表示第i层结构高度;Fj表示第j层的荷载;ωi表示第i层的质量;n为结构层数;Vb为基底水平剪力总和。

基于位移的推覆是直接将目标位移作为设计值，这样在设计初期就明确了设计结构的性能水平［2－3］。研究表明:结构的性能状态和损伤程度主要取决于结构位移［4］，位移加载模式包括在结构顶层施加位移和在结构各层均施加位移［5］。

MPA法是由 Chopra［6］提出的一种全新的Pushover方法，即多模态 Pushover方法(简称MPA)。该方法是根据结构各阶振型的侧向荷载模式对结构进行多次推覆分析，忽略结构屈服后各阶振型之间的耦合，按照一定的法则得到结构考虑多阶振型影响下的弹塑性地震响应。由于该方法考虑了结构高阶振型的影响，计算精度提高。

3 大跨悬挑结构的计算模型

提取的悬挑结构简化模型主楼高35 m，层高均为5 m，共7层，其中 5－7层为带有大跨度悬挑层，悬挑跨度12 m。建筑设防烈度为7度，设计地震分组为I组，抗震设防类别为甲类，为框架剪力墙结构。每层楼板开有12 m×18 m的大洞，楼板开洞四周布置有K形中心支撑。梁、柱和剪力墙的混凝土等级为C50，钢筋采用HRB400。主梁截面为400 mm×800 mm，柱截面为800 mm×800 mm。悬挑层两侧布置有单杆偏心支撑，耗能梁长取为0．5 m。悬挑梁截面为1 200 mm×600 mm，悬挑柱截面为800 mm×800 mm，边环梁和偏心支撑选用Q235B，截面为工字形。剪力墙墙厚为300 mm。悬挑层楼板的板厚取150 mm，标准层楼板板厚均取100 mm，标准层楼板钢筋间距为150 mm，悬挑层楼板钢筋间距为100 mm。

采用通用有限元软件ABAQUS对简化悬挑结构进行了时程分析和静力弹塑性分析，梁柱采用二次梁单元B32模拟，楼板和剪力墙采用S4R单元模拟，结构施加恒载为5 kN/m2，活荷载为2 kN/m2。混凝土本构关系模型采用分段直线描述［7］，钢筋本构关系采用理想弹塑性的二折线模型，钢筋在进入强化段卸载后考虑包兴格效应，本构模型见图1。

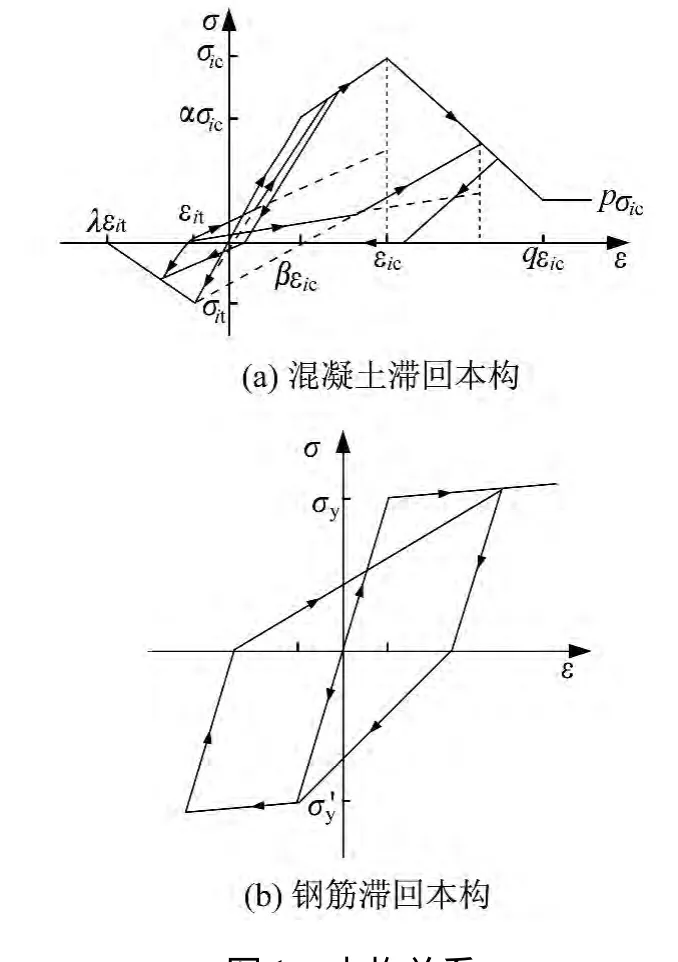
图1 本构关系Fig．1 Constitutive relationships

悬挑层平面、标准层平面、结构立面分别见图2—图4，构件截面见图5，图6为简化悬挑结构的有限元模型。经计算结构前4阶周期分别为0．52 s、0．34 s、0．33 s和 0．13 s，前两阶振型为横向平动和纵向平动，第三阶为结构整体的水平扭转，第四阶振型为悬挑部分集中的竖向变形，前五阶振型图见图7。

4 Pushover分析和时程分析对比

罕遇地震时程分析选取El Centro波和Taft波，按7度抗震设防，加速度时程最大值为2 200 mm/s2，分析采用经典 Rayleigh阻尼，阻尼比取5%，质量比例阻尼因数α=0．152 1，刚度比例阻尼因数β=0．005 4。在基于力控制的静力推覆过程中，各层竖向地震力按各层重力荷载代表值的15%考虑，且在推覆中与侧向力等比例增大;基于位移控制推覆时，按结构在多遇地震下顶点位移达到最大时的侧向水平位移模式进行推覆;MPA法中分别按结构的前三阶振型模式进行推覆，并按照SRSS进行组合。

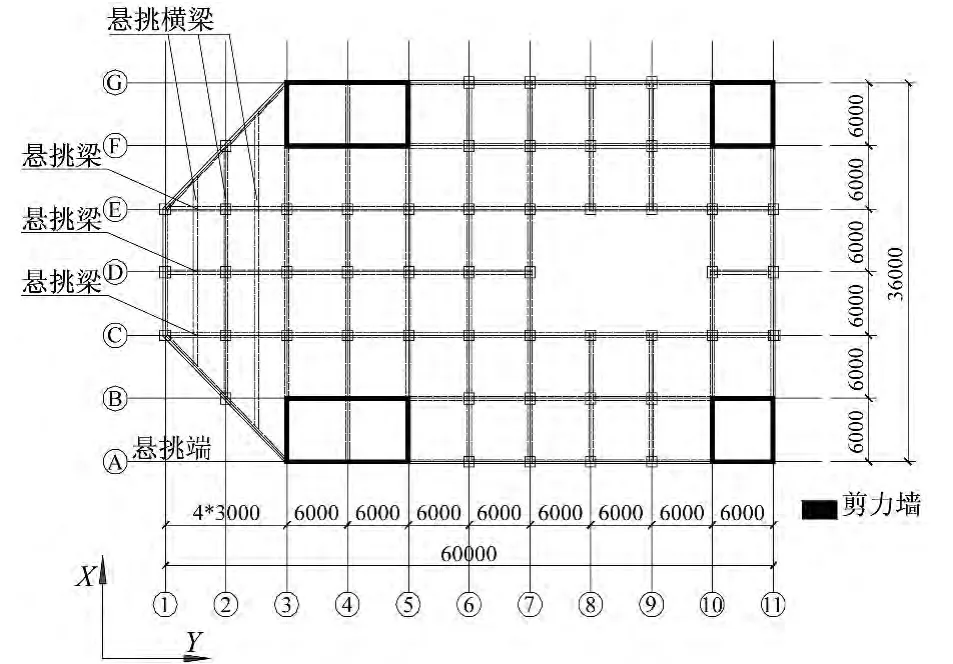
图2 悬挑层平面图(+30．0 m)(单位:mm)Fig．2 Plan of cantilever floor(+30．0 m)(Unit:mm)

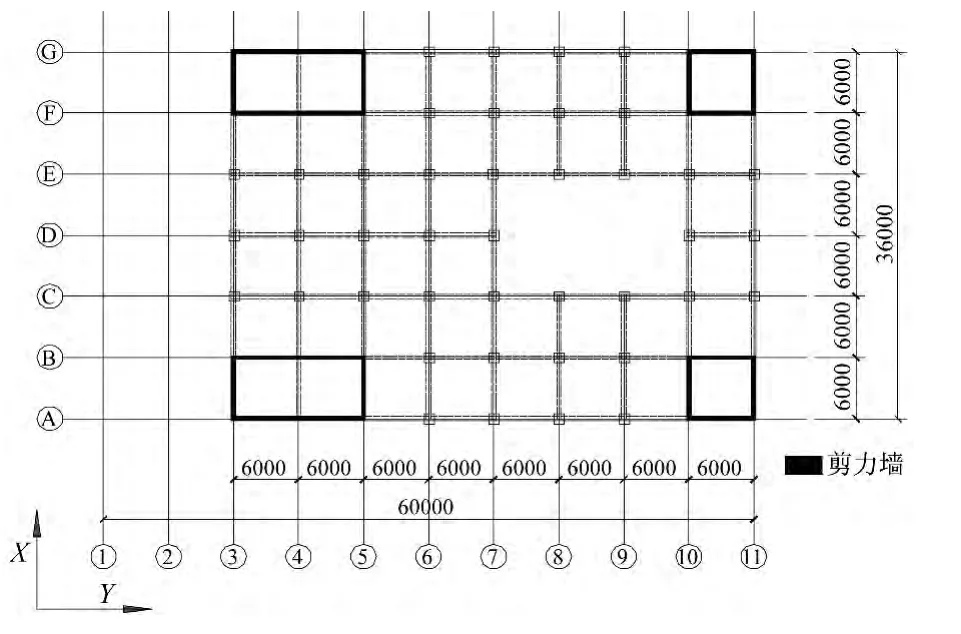
图3 标准层平面图(+15．0 m)(单位:mm)Fig．3 Plan of standard floor(+15．0 m)(Unit:mm)

图4 楼板开洞处X向中心支撑布置示意图(单位:mm)Fig．4 Arrangement of concentrical braces around the openings of floor in the X direction(Unit:mm)

图5 构件截面(单位:mm)Fig．5 Cross sections of members(Unit:mm)

图6 框剪悬挑结构有限元模型Fig．6 Finite element model of cantilever frame-shear wall structure

4．1 最大层侧移沿楼层分布

图8 为不同模式下顶层A点的侧移图。从图中可看到，在结构X向，力加载下的楼层侧移大于时程分析结果，位移加载下楼层位移最大，MPA法下楼层侧移较时程分析结果小。在结构Y向，振型组合侧力模式和MPA法下楼层侧移较时程分析结果大，倒三角侧力模式下结果较小。总体来看，悬挑层在力加载模式和MPA法下的变形误差较小，标准层在位移加载模式下的变形误差较小。

图7 框剪悬挑结构前五阶振型Fig．7 Top five modes of cantilever frame-shear wall structure

图8 楼层位移Fig．8 Storey displacement of structure

4．2 最大层间位移角沿楼层分布

图9 为结构在各种静力推覆和时程分析下结构的层间位移角分布。由图可见，结构在不同地震波下的层间变形差异较大。在结构X向，悬挑层在力加载下较时程结果小，在位移加载下较时程结果大。在结构Y向，层间变形规律与X向较相似，标准层在振型组合侧力模式下层间变形较时程结果大，MPA法下各层层间变形均较时程结果大，比较来看，位移加载下误差最小。

图9 层间位移角分布Fig．9 Distribution of inter-storey drift

总的来说，结构对称向，悬挑层在振型组合分布力加载模式和倒三角分布力模式下误差最小，标准层采用力控制和位移控制结果较安全;结构非对称向采用位移控制准确性较高。

4．3 最大层间剪力沿楼层分布

按各层水平力占基地总剪力的比例得到相对值，见图10。在结构X向，悬挑层在力加载和MPA下的楼层力分布与时程结果较一致，位移加载下的楼层力较大;标准层在力加载下楼层力较时程结果大，MPA与Taft波结果较一致，位移加载结果较时程结果小，总体看来，位移加载结果与时程结果有较大差别，力加载和MPA与时程结果较一致。结构Y向与X向相似，总的看来，悬挑层在振型组合分布力模式下误差最小，在位移加载下误差最大，标准层在力加载下误差结果较准确，MPA法与倒三角分布力模式的结果基本一致。

4．4 悬挑部分受力性能

在对悬挑结构进行罕遇地震时程分析和双向静力推覆分析时，发现悬挑部分的偏心支撑受力远大于悬挑柱的受力，说明悬挑部分的偏心支撑是联系悬挑层的主要竖向构件;悬挑梁在与主体结构相交处受力远小于偏心支撑的受力，可见在地震作用下悬挑部分两侧的偏心支撑可以起到第一道抗震防线的作用，只要偏心支撑在大震作用下不过早屈服，并在屈服后保持良好的延性，就能保证悬挑主梁这一核心构件的安全。

图10 楼层力分布Fig．10 Distribution of floor force

5 结论

通过对大跨悬挑结构进行静力推覆分析和地震时程分析，分析了大跨悬挑结构的抗震性能，并讨论了不同的静力推覆分析对大跨悬挑结构的准确性。

(1)在地震作用下，大跨悬挑结构的底层容易形成薄弱层，需要加强配筋来提高变形耗能能力。

(2)在预测结果变形时，悬挑层采用力控制和MPA误差较小，标准层采用位移控制误差较小。在预测结构层间变形时，结构对称向采用力控制较准确，非对称向采用位移控制较准确。预测层间剪力时采用力加载和MPA较为准确。

(3)悬挑部分两侧设置偏心支撑可提高悬挑部分的冗余度，提高悬挑主梁的安全度。

［1］ 朱慈勉，应丹君．竖向不规则结构Pushover分析的侧向荷载分布模式研究［J］．结构工程师，2009，25(3):29-34．Zhu Cimian，Ying Danjun．Research on Lateral patterns in pushover andlysis of vertically irregular structrues［J］．Structural Engjineers，2009，25(2):29-34．(in Chinese)

［2］ 汪梦甫，王锐．基于位移的结构静力弹塑性分析方法的研究［J］．地震工程与工程振动，2006，26(5):73-80．Wang Mengfu，Wang Rui．Study on displacementbased pushover procedure［J］．Earthquake Engineering and Engineering Vibration，2006，26(5):73 －80．(in Chinese)

［3］ 蒋建．基于性能抗震设计方法与基于承载力抗震设计方法比较研究［J］．结构工程师，2008，24(4):52-57．Jiang jian．Comparitsve Study on Performance-based seismic design method and bearing capacity-based clesign method［J］．Structural Engineers，2008，24(4):52-57．(in Chinese)

［4］ Priestley M J，Kowalsky M J．Direct displacement based seismic design of concrete buildings［J］．Bulletin of the New Zealand Society for Earthquake Engineering，2000，33(4):421-44

［5］ 李琪，顾荣蓉，缪志伟，等．基于位移模式静力弹塑性分析方法的研究［J］．河海大学学报(自然科学版)，2005，33(6):86-89．Li Qi，Gu Rongrong，Miao Zhiwei，et al．Displacementpattern-based static elasto-plastic andlysis method［J］．Journal of Hohai University(Natural Sciences)，2005，33(6):86-89．(in Chinese)

［6］ Chopra A K，Goel R K．A modal pushover analysis procedure to estimate seismic demands for buildings theory and preliminary evaluation［R］．Berkeley，CA:Report No．PEER 2001/03，Pacific Earthquake Engineering Research Center， University of California，2001．

［7］ Li K N．Three dimensional nonlinear dynamic structural analysis computer program package［M］．User Manual，Canny Consultants PTE ltd，Oct，1996．