对柳比莫夫摆运动规律的探讨*
2015-03-21张邦健苗峰张传武
张邦健,苗峰**,张传武
(西南民族大学电信学院,四川成都610000)
对柳比莫夫摆运动规律的探讨*
张邦健,苗峰**,张传武
(西南民族大学电信学院,四川成都610000)
推出了柳比莫夫摆的动力学特征方程,通过对动力学方程的分析证明了柳比莫夫摆并非摆动而是做圆周运动,得出了小球运动的特征椭圆,并利用特征椭圆分析小球运动的规律并给出了周期公式。
柳比莫夫摆;特征方程;特征椭圆;周期
1 问题的提出
柳比莫夫摆是研究热对流问题的一个简化模型[1-3]。图1所示为柳比莫夫摆模型图,框架上悬挂小球,小球质量为m,框架质量为M。将小球移开平衡位置并给其一切向速度,同时释放框架。当时,小球会绕框做匀速圆周运动[4]。如果m与 M可比拟时,小球又将做怎样的运动呢?文献[5]已对这个问题有了一定的探讨,本文将进一步分析小球的运动规律。
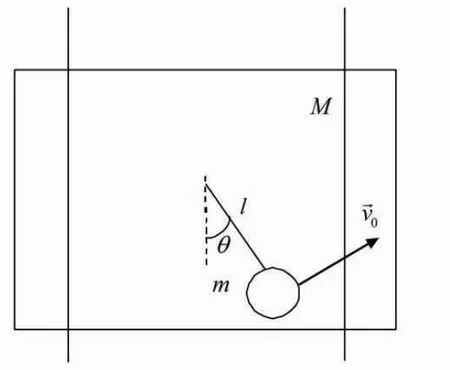
图1 柳比莫夫摆装置图
2 小球运动规律的特征方程
关于θ的大小,作如下规定:从y轴负半轴开始逆时针旋转一定的角度与摆线重合,这个角度就称为θ。笔者采用隔离法来建立方程,首先以框为研究对象,该物体受到三个力的作用,即重力,绳对框的拉力,杆对框的作用力,如图2所示
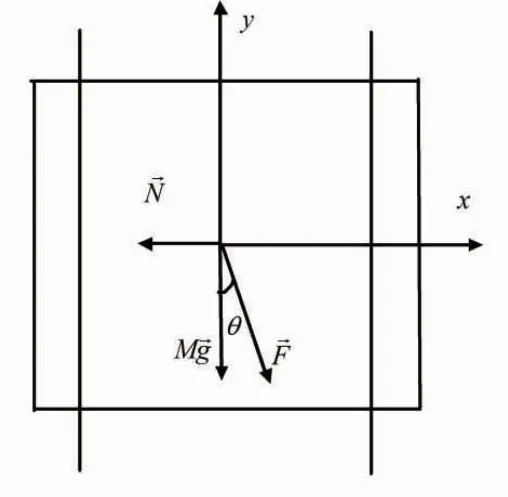
图2 框的受力示意图


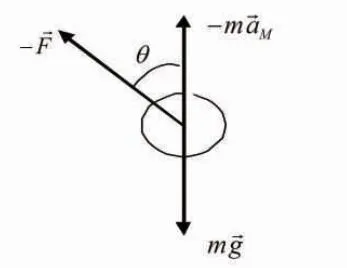
图3 小球的受力示意图

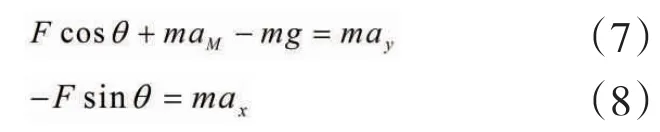
利用x、y方向的分速度与夹角的关系可知

3 证明小球做圆周运动
3.1 细绳始终是绷直的

图4 绳弯曲时球的运动情况
3.2 小球的运动永不反向
从(14)可以看出:小球相对于框的速度永不为零也不趋近于零,否则,与(14)矛盾。由于小球的速度不能突变,所以小球的运动将不会反向。
3.3 小球的位移没有极限
现假设A点是小球的极限位置,可以分两种情况:①小球相对于框静止在A点;②小球相对于框无限逼近A点。对于①,显然有小球相对于框的速度为零。对于②,前面已经论述了小球的运动永不反向,而小球又无限逼近A点,故必然有小球相对于框的极限速度也为零,同样与(14)矛盾。可见小球的位移没有极限。
综上所述,由于绳在任意时刻都是绷直的,且小球的运动永不反向,小球的位移又没有极限,则相对于框,小球必然做圆周运动。
4 小球运动的特征椭圆
4.1关系

其图像如图5所示

图5 特征椭圆1(关系)
下面再进一步地讨论这个椭圆与小球运动规律之间更深层次的联系。从图5中可以得出


4.2关系
若将图5中的椭圆做这样的变换:保持各点的纵坐标不变,横坐标变为原来的倍,则将原来的椭圆拉成了一个半径为的圆,如图6(a)所示。
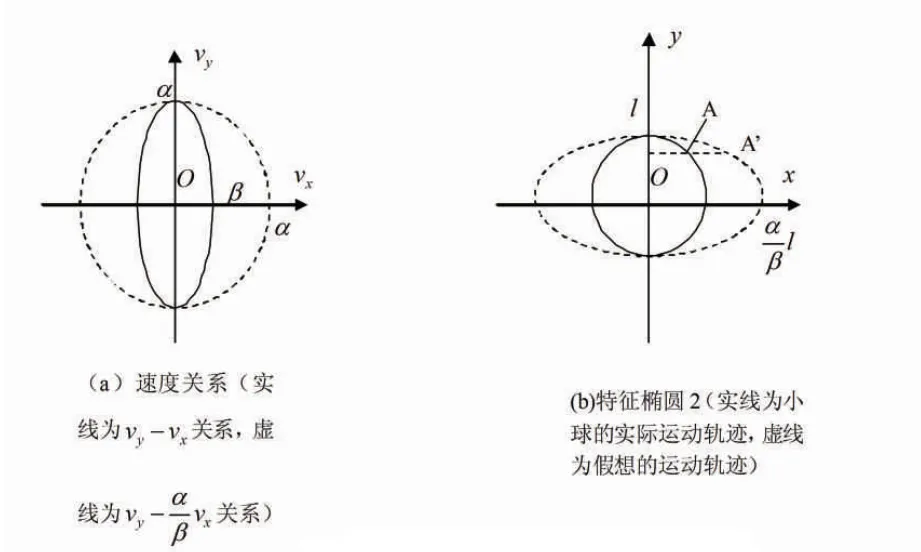
图6 位速变换图
5 柳比莫夫摆的性质
根据特征椭圆,可以发现一些柳比莫夫摆的性质:
5.1 小球速度的变化规律
根据特征椭圆1,有小球与悬点相平时速度最大,在最高和最低位置时速度最小。从水平位置经过最低(高)点到水平位置时,水平分速度从零到最大再变为零,而竖直分速度从最大变为零再变到最大。
5.2 小球运动的周期
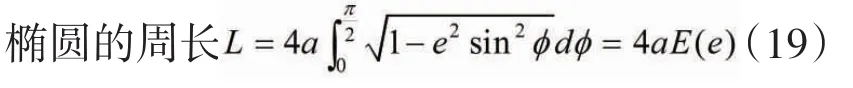
5.3 小球的运动学方程

5.4时小球的周期及周期公式的检验

下面由以上所求周期公式计算该情形下的周期:

即小球质量远远小于框的质量时的周期公式可作为柳比莫夫摆周期公式的特例给出,同时也说明了柳比莫夫摆周期公式的正确性。
6 结论
本文利用经典力学理论推出了柳比莫夫摆的动力学特征方程及特征椭圆,并通过特征椭圆进行分析得出了及之间的关系。证明了柳比莫夫摆做非匀速圆周运动,并得到了柳比莫夫摆运动的周期公式。本文结果研究表明,时的柳比莫夫摆周期公式可作为柳比莫夫摆运动周期公式的特例给出。
注释及参考文献:
[1]Pavan K.Shukla,R.Narayanan.The effect of time-dependent gravity with multiple frequencies on the thermal convective stability of a fluid layer[J].International Journal of Heat and Mass Transfer,2002(45):4011-4020.
[2]D.Lyubimov,A.Cherepanov,T.Lyubimova.Behavior of a drop(bubble)in a non-uniform pulsating flow[J].Advances in Space Research,2002,4(29):667-672.
[3]Mark I.Shliomis.Nonlinear Dynamics of a Ferrofluid pendulum[J].Physical Review Letters,2004,7(23).
[4]漆安慎,杜婵英.普通物理教程-力学[M].北京:高等教育出版社,2005:112,477.
[5]张邦健,黎昌金,陈永强,等.对柳比莫夫摆运动规律的研究[J].西部教育研究,2010,4:108-110..
[6]《现代数学手册》编纂委员会.现代数学手册-经典数学卷[M].武汉:华中科技大学出版社,1999:372-377.
The Discussion of the Lyubimov Pendulum’s Law of Movement
ZHANG Bang-jian,MIAO Feng,ZHANG Chuan-wu
(School of Electronic and Information Engineering,Southwest University for Nationalities,Chengdu,Sichuan 610000)
In this paper,we have derived the kinetic characteristic equation of the Lyubimov Pendulum’s and have proved that it will circle.It is concluded eigenellipse of the small ball movement.Making use of the eigenellipse,it has also solved the Period’s analytical expressions of the Pendulum’s movement and provided its cycle formula.
Lyubimov Pendulum’s;characteristic equation;eigenellipse;period
O314
A
1673-1891(2015)03-0017-03
2015-03-27
西南民族大学2014年教育教学改革青年项目(项目编号:2014QN05)。
张邦健(1990-),男,四川成都人,硕士,研究方向:材料物理。**为通信作者苗峰博士。
