压缩感知及其在超声成像中的应用
2015-03-21张琼李斌李德来
张琼 李斌 李德来
1 广东省汕头大学工学院 ( 汕头 515063)
2 汕头市超声仪器研究所有限公司 ( 汕头 515041)
0.引言
由于超声成像具有实时、无创、成本低等优点,已经成为主流的医疗成像检测手段之一[1]。随着对超声图像后期调节、参数优化和远程会诊等需求的增加,就要求所存储的数据保留尽可能多的原始信息。最理想的情况是可以直接实时的保存原始图像的射频线数据,这样后期参数调节的空间和自由度就非常大,能够满足更多的实际应用需求。但是奈奎斯特(Nyquist-Shannon)采样定理指出:为了保证能够完全的恢复原信号,信号的采样速率必须要大于或等于两倍的信号带宽,否则信号频谱会出现混叠,不能准确的恢复出原信号[2]。一般来说超声成像所用频率的范围为1~20MHz,根据奈奎斯特采样定理,最低采样率应该为40MHz,考虑到实际工程应用,一般会选择60MHz 或更高。这样在一个探测深度为200mm 的超声成像系统中1 秒钟产生的超声射频回波线数据量约为1G 字节。如此大的数据量对数据的实时存储、传输和保存等都是很大的挑战。
使用传统的数据压缩算法可以一定程度上减少数据量的大小,但是数据压缩的过程中会产生很多无用的运算,降低了压缩的效率;而且要想得到高精度的重建原始数据时压缩效率急剧下降[3~4]。随着图像和信号处理的发展,Candès, Donoho, Tao 和Romberg 等人在2004 年提出了压缩传感(compressive sensing,CS)的概念,随后他们构造了压缩传感的实现算法并通过实验证明该理论的正确性及其巨大的应用前景[5~6],并被美国科技评论评为2007 年度十大科技进展。该理论表明,在一定条件下,以低于奈奎斯特采样频率对稀疏信号或图像进行压缩后,仍然能够很好的重建原信号或原图像。
本文将压缩传感技术应用到超声成像的射频回波线数据存储中,提出基于压缩感知的超声射频回波线数据压缩算法。该算法能大大降低数据的大小,相比于其他算法,不需要通过计算所有分量后再对计算出来的信号进行排序和编码,提高了压缩效率,在压缩数据的同时可以高精度的重建原始信号。
1.压缩传感理论
1.1 传统的信号压缩方法
传统的信号压缩是将信号由时域或空间域投影到另一个更加逼近原信号特征的域,使其可以用尽量少的系数逼近原信号。例如,一个由少数几个频率构成的信号,在时域上需要用很多个点来表示,但是如果将其变换到频域中就只需要用几个频点来表示。在数据压缩存储时只需存储对应的几个频域点的数据,在重建时进行相应的反变换就可以恢复原来的信号。这样大大降低了所需存储的数据大小。一般情况,设一维有限信号,ψ 是RN空间中的一组完备正交基,则信号x 可表示为:
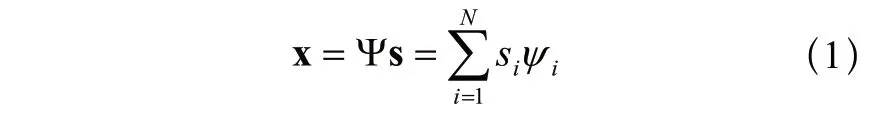
其中s = [s1,s2,...,sN],Ψ = [Ψ1|Ψ2|Ψ3|...|ΨN],s 为x 在超完备正交Ψ 上的投影,即s = (x,Ψi)。
若s 中非零系数或数值较大的si的数目为K,系数为零或数值很小的si的数目为N–K 。当K < 与上述方式不同,压缩传感技术直接利用测量矩阵直接获取稀疏信号或者可压缩信号的特征信息[7~8]。设一维实信号x 是 K 稀疏,利用 M×N (K 将 (1) 式代入 (2) 式得: 令Θ = ФΨ,则(3)式可表示为 其中s 为K 稀疏的。 对于(4)式,一般来说,要想从M×1 维的信号y 中直接恢复N×1 维信号x 是不可能的,因为在数据压缩时M< 对于合成后的超声回波射频数据,考虑同一帧图像中相邻线之间的相关性比较大,我们将一帧图像分为若干个子区域,每个子区域的线数均相等。在数据存储时对于一个子区域中的超声射频回波线数据,直接计算其在随机采样矩阵上的投影,得到压缩后的数据。在数据还原时对压缩后的数据求解式(5)、(6)就能得到原信号的逼近。 图1-a 为5MHz 发射的线阵探头采集到的超声原始线数据的一个子区域,为了保留线之间的相关性,我们选择子区域的大小为32 条线。每线640 点,每点用3 字节表示,如果直接将这些原始的RF 线数据进行存储需要的数据大小为:32x640x3=61440 字节。图1-b 为本文当使用的随机采样矩阵。图1-c 为由式(2)得到的压缩后的32 线回波信号,压缩后子区域中的每线只需用70个点就可以很好地恢复原始线数据,压缩后的数据大小为32x70x3=6720Byte,约为原数据的11%,大大减少了存储的数据量。图1-d 为使用式(5)、(6)重建得到的原始32 线回波数据。图2 为重建前后各线的误差情况,从图中可以看出重建后的射频线回波信号相对于原始信号误差小于总能量的0.2%,表明压缩过程丢失的信息很少。 图1. 32 线射频回波数据的压缩和解压图 图2. 32 线射频数据重建前后的误差图 如何实时、高效地存储超声成像射频回波线数据是实现超声成像后期调节、参数优化和会诊的关键。本文利用目前信号采样和压缩领域全新的压缩感知理论,结合超声射频回波线数据的相关性和稀疏性,提出基于压缩感知的超声射频回波线数据压缩算法。该算法能大大降低数据的大小,相比于其他压缩算法,该算法相比于其他算法,不需要通过计算所有分量后再对计算出来的信号进行排序和编码,只需直接计算原始线数据在少数几个随机采样矩阵上的投影。实验结果表明,本文算法可以实现实时、高效地对超声回波中的射频线数据进行压缩。 [1] A. Webb, Introduction to Biomedical Imaging. John Wiley & Sons, Hoboken, 2003. [2] 郑君里,杨为理,应启珩.信号与系统-上下册(第二版).北京:高等教育出版社,2000 年. [3] 孙家宝,郭峰林,薛伟,等. 基于小波变换的时空数据压缩方法.武汉工业学院学报.32(3):74-78, 2013. [4] 万建伟,粘永健,苏令华,等. 高光谱图像压缩技术研究进展.信号处理, 26(9):1397-1407,2010. [5] Candès E, Tao T. Decoding by linear programming, IEEE Trans. on Information Theory, 51(12):4203-4215, 2005. [6] Justin Romberg, Imaging via compressive sampling. IEEE Trans. on Signal Processing, 25(2):14 - 20, 2008. [7] Marco F. Duarte, Mark A. Davenport, Dharmpal Takhar, Jason N. Laska. Ting Sun, Kevin F. Kelly, Single-Pixel Imaging via Compressive Sampling, I IEEE Trans. on Signal Processing,83-91 , 2008. [8] Richard Baraniuk, Compressive sensing. IEEE Trans. on Signal Processing, 24(4):118-121, 2007. [9] Joel Tropp and Anna Gilbert, Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. on Information Theory, 53(12): 4655-4666, 2007. [10] David Donoho and Yaakov Tsaig, Fast solution of ell-1-norm minimization problems when the solution may be sparse. Stanford University Department of Statistics Technical Report 2006-18, 2006.1.2 压缩感知

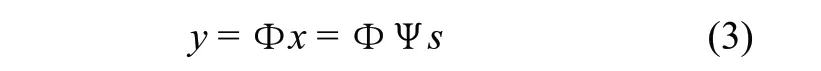


2.压缩感知在超声射频线数据存储中的应用


3.结论
