2缸发动机平衡机理研究及悬置系统优化设计
2015-03-21余良渭上官文斌唐颖李锦庭
余良渭, 上官文斌, 唐颖, 李锦庭
(1. 华南理工大学机械与汽车工程学院, 广东 广州 510641; 2. 上汽通用五菱汽车股份有限公司, 广西 柳州 545007)
·设计计算·
2缸发动机平衡机理研究及悬置系统优化设计
余良渭1, 上官文斌1, 唐颖2, 李锦庭2
(1. 华南理工大学机械与汽车工程学院, 广东 广州 510641; 2. 上汽通用五菱汽车股份有限公司, 广西 柳州 545007)
以2缸发动机为研究对象,分析发动机曲柄活塞机构的运动规律,推导发动机在实际工作时产生的不平衡激励力和力矩,研究2缸发动机的旋转惯性力和往复惯性力的平衡方法,对一台2缸发动机在不同平衡条件下产生的激励进行数值模拟。在此基础上,建立2缸发动机悬置系统优化模型,以悬置系统的固有频率、能量解耦率和悬置动反力为优化目标,用序列二次规划法进行多目标的优化,对一台2缸柴油机进行了悬置系统优化设计。分析结果表明该优化方法可以有效减少发动机传递给车身的激励。
2缸发动机; 平衡机理; 悬置系统; 多目标优化
目前轿车向着轻量化和燃油经济化的方向发展,2缸发动机在轿车、微型车上的应用将越来越普及。但2缸发动机的平衡性较差,发动机本身的激振力较大,对整车的平顺性不利。
要减小2缸发动机的激振力,需要减小发动机自身不平衡激励。发动机的曲柄活塞机构工作时产生的旋转惯性力可以通过在曲轴上相应位置加装平衡重来平衡,而活塞运动的往复惯性力无法通过曲轴上的平衡重完全平衡,需要通过外加平衡轴来平衡[1]。 Karabulut[2]用一个3自由度的动态模型对一台2缸四冲程发动机进行数值模拟,总结了曲轴上平衡质量的确定方法;Kim[3]提出平衡轴上平衡质量的大小、安装位置的优化策略。另一方面,悬置系统的设计会很大程度地影响发动机传递给车身的振动大小。通过优化悬置的刚度、安装位置和角度,可以使2缸机自身激励传递给车身的力最小。上官文斌等从系统的固有频率和能量解耦率出发,深入研究了动力总成悬置系统的设计及优化方法[4-7]。Akei等的研究表明,发动机悬置的刚度及安装布置对悬置系统的整体减振性能有明显影响[8],而使用序列二次规划法(SQP)进行悬置系统的优化设计可以有效减弱发动机经悬置传递给车身的力[9-10]。
本研究分析了2缸发动机缸体所受的不平衡激励力(矩),研究曲轴上加平衡重及平衡轴的平衡机理,分析2缸发动机悬置系统在不同平衡条件下产生的自身激励;针对某2缸柴油机,以其悬置系统固有频率、能量解耦率、悬置动反力为优化目标,以悬置的三向刚度和安装位置为控制变量,建立2缸机悬置系统的多目标优化模型,得到悬置刚度及安装位置的优化结果。
1 2缸发动机平衡性分析
每个缸内曲柄连杆机构的运动可以分为曲柄绕曲轴的旋转运动和活塞、连杆沿气缸内壁的往复运动。发动机缸体受到曲柄旋转运动产生的旋转惯性力、活塞组件往复运动产生的往复惯性力、缸内气体燃烧的气体力三者的共同作用。
单个曲柄连杆机构的旋转惯性力Fr、往复惯性力Fj(见图1)为
Fr=mrrω2,Fj=mjrω2(cosα+λcos2α)。
(1)
式中:ω为曲轴转动的圆频率;r为曲柄半径;mr为每缸位于曲柄销中心并绕曲轴轴线的旋转运动质量;mj为每缸位于活塞销中心沿气缸中心线的往复运动质量;α为曲拐转角;λ=r/l为连杆比,l为连杆大小头的中心距。往复惯性力包括一阶往复惯性力Fj1和二阶往复惯性力Fj2两部分:
Fj1=mjrω2cosα,Fj2=mjrω2λcos2α。
(2)
对于常见的2缸发动机,其曲柄分布见图2,发动机坐标系的X轴沿曲轴中心线,指向发动机前端,Z轴平行于气缸轴线,指向缸盖,Y轴根据右手定则确定。
两个缸的旋转惯性力分别为Fr,1,Fr,2,大小相等,方向沿各自的曲柄,其合力Fr∑的大小为
Fr∑=|Fr,1+Fr,2│=2mrω2。
(3)
两个缸的一阶往复惯性力为Fj1,1,Fj1,2,二阶往复惯性力为Fj2,1,Fj2,2,其大小分别为
Fj1,1=mjrω2cosα,Fj1,2=mjrω2cos(α-360°),
(4)
Fj2,1=mjrω2λcos2α,
Fj2,2=mjrω2λcos(2α-720°)。
(5)
两个缸的一阶往复惯性力合力Fj1∑、二阶往复惯性力合力Fj2∑的大小为
Fj1∑=|Fj1,1+Fj1,2│=2mjrω2·cosα,
(6)
Fj2∑=|Fj2,1+Fj2,2│=2mjrω2λcos2α。
(7)
将合力Fr∑,Fj1∑,Fj2∑分别沿发动机坐标系各轴分解,则缸体在发动机坐标系下受到的作用力为
Fy=-Fr∑·sinα=-2mrrω2·sinα,
(8)
Fz=Fj1∑+Fj2∑+Fr∑cosα=2mjrω2·
cosα+2mjrω2λcos2α+2mrrω2·cosα。
(9)
以两个缸的中心点为参考点,则两个缸的旋转惯性力、一阶往复惯性力、二阶往复惯性力产生的力矩矢量和为0。缸体在发动机坐标系下受到的作用力矩见图3,其中Mx为发动机的输出力矩。以两个缸中心点为参考点时,My,Mz为0。
工程中发动机激励一般以动力总成质心坐标系为参考,一般情况下2缸发动机的两个缸的中心点与动力总成质心不重合,设2缸机的两个缸中心点在整车坐标系下的坐标为 (XE,YE,ZE),动力总成质心在整车坐标系下的坐标为(XCG,YCG,ZCG),以动力总成质心为参考点,则2缸发动机缸体受到的不平衡力Fy,Fz产生的力矩为
My=Fz×(XCG-XE),
(10)
Mz=Fy×(XCG-XE),
(11)
Mx=-Fy×(ZCG-ZE)-Fz×(YCG-YE)。
(12)
2 2缸发动机的平衡方法
2缸发动机产生的旋转惯性力Fr∑和一阶往复惯性力Fj1∑数值上比较大,对发动机平衡性影响明显,一般采用曲轴加平衡重和外加平衡轴的方式进行平衡。
2.1 曲轴平衡重平衡分析

(13)
(14)
(15)
曲轴加平衡重后2缸发动机受到的不平衡力和力矩见表1。

表1 曲轴加平衡重后2缸机受到的不平衡力(矩)
2.2 一阶平衡轴平衡分析

(16)
(17)
(18)
由于平衡轴与曲轴之间有偏心距离,平衡轴上平衡重产生的旋转惯性力合力会产生绕X轴方向的附加力矩(见图8)。
(19)
曲轴加平衡重且加一阶平衡轴后2缸发动机受到的不平衡力见表2,受到的不平衡力矩见表3。
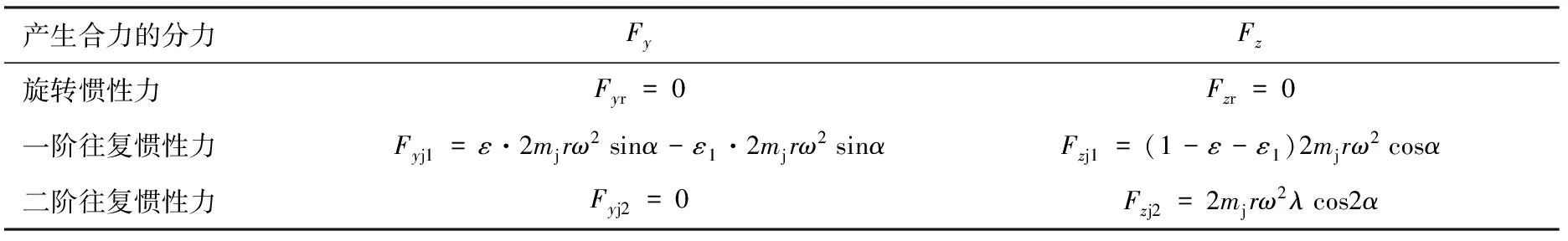
表2 曲轴加平衡重且加一阶平衡轴后2缸机受到的不平衡力

表3 曲轴加平衡重且加一阶平衡轴后2缸机受到的不平衡力矩
3 2缸发动机悬置系统优化设计
下面以一款2缸柴油机为例,分析该发动机在不同平衡条件下悬置系统的受力情况,使用序列二次规划法进行悬置系统的多目标协同优化,并对比分析优化前后的悬置受力的情况。
3.1 2缸发动机悬置系统参数
图9示出一发动机纵置的后驱轿车上的动力总成悬置系统。该动力总成使用三点悬置支撑,O—X0Y0Z0为整车坐标系,CG为动力总成质心,动力总成质心坐标系如图中CG—XYA所示,OE—XEYEZE为以发动机两个缸的中心点为原点建立的发动机坐标系。
该2缸发动机的质量及惯性参数见表4,发动机曲柄连杆机构参数见表5,各悬置在局部坐标系下的初始静刚度及悬置在汽车坐标系中的安装位置见表6,实测该2缸发动机的缸压曲线见图10。

表4 动力总成的质量及惯性参数

表5 曲柄连杆机构参数

表6 悬置的初始刚度及在汽车坐标系中的安装位置
该2缸机动力总成的质心在整车坐标系下的坐标为(208,-13,7),发动机采用三点悬置支撑的形式,两个前悬置V型布置,主要起支撑和防扭作用,后悬置辅助支撑。该悬置系统在动力总成重力作用下的静态位移见表7。一般动力总成悬置系统要求预载位移小于5mm,从表7可以看出,该悬置系统满足静态平衡要求。

表7 悬置静态预载位移
3.2 不同平衡条件下的发动机激励分析
在不采取任何平衡措施的情况下,发动机的曲柄活塞机构的旋转惯性力、一阶往复惯性力、二阶往复惯性力都处于不平衡的情况,此时2缸发动机由于曲柄连杆机构运动的惯性力产生Fy,Fz两个方向的不平衡力激励(见图11),同时还有Mx,My,Mz3个方向的不平衡力矩激励(见图12)。
曲轴上加平衡重可以实现100%平衡旋转惯性力和按一定比例平衡一阶往复惯性力。用于平衡一阶往复惯性力的平衡重会产生水平方向的附加力,故一般用曲轴加平衡重的方式平衡50%的一阶往复惯性力。这种平衡情况下发动机整体结构简单,产生的不平衡激励见图13和图14。
在加装平衡轴的情况下,2缸发动机的不平衡力激励Fz(见图15)只剩下二阶往复惯性力,且二阶往复惯性力较小。此时发动机产生的不平衡力矩激励见图16。
3.3 悬置系统优化设计
在设计发动机悬置系统时,一般将动力总成简化为空间中的六自由度刚体模型,主要考虑其六阶固有频率和六个自由度的解耦率。悬置固有频率和解耦率计算方法详见文献[11],考虑固有频率和解耦率的优化目标函数形式见文献[7]。对于2缸发动机,在不同平衡条件下自身激励不同,从而悬置受力也不同。本研究在设计2缸发动机的悬置系统时,同时考虑固有频率、能量解构率及悬置动反力3个方面的要求,建立目标函数的表达式为
式中:ω1,ω2,ω3分别为总的固有频率权系数、总的解耦率权系数和总的动反力权系数;αi为第i个自由度固有频率的权系数,βi为第i个自由度的解耦率的权系数,γi为第i个悬置的动反力的权系数。
Si为各阶固有频率与目标频率的差值,具体定义式如下:

理想情况下悬置系统各自由度的解耦率最大为100%,由于布局的限制,实际中难以达到100%,一般设定解耦率下限值decli为75%,从而定义各自由度的解耦率在优化目标函数中的表达式Ti为
本研究取2缸机在完全平衡状态(旋转惯性力,一阶、二阶往复惯性力完全平衡)下悬置的动反力作为“动反力目标值”,试图通过对悬置的优化,使得2缸机在不平衡或者部分平衡状态下,悬置点的动反力等于或者小于发动机完全平衡时悬置点的动反力。
悬置系统的固有特性取决于悬置的刚度、安装位置和角度等。本算例中的2缸柴油机的悬置安装角度已经固定,故取3个悬置的三向刚度和安装位置为优化变量,设为
{X}={ku1,kv1,kw1,x1,y1,z1,…
kui,kvi,kwi,xi,yi,zi,…}。
式中:kui,kvi,kwi为第i个悬置的三向静刚度值;xi,yi,zi为第i个悬置的安装位置。
考虑悬置的可制造性,悬置的静刚度有上下限的约束,不同方向之间的刚度值有一定的比例关系约束。2缸机的悬置刚度比例约束见表8。悬置安装位置限制为初始位置坐标±5mm的范围。

表8 悬置的刚度比例约束
本研究使用序列二次规划法(SQP),将此问题转化为简单的二次规划问题进行迭代求解。优化后的悬置刚度和安装位置信息见表9。

表9 优化后悬置的刚度及安装位置
本研究中的2缸发动机实际采用了曲轴加平衡重且外加一阶平衡轴的方式进行平衡,在此基础上进行了悬置系统的优化设计,优化后的悬置动力情况见图17和图18。
在不采取任何平衡措施的情况下,2缸发动机会产生较大的不平衡激励,导致3个悬置的受力都较大。在曲轴上加平衡重,平衡了100%的旋转惯性力和50%的一阶往复惯性力,悬置的受力情况明显变好。在此基础上外加一根平衡轴,用于平衡50%的一阶往复惯性力,悬置受力情况进一步改善。在发动机的机械结构确定之后,发动机自身的不平衡激励已经无法改变,此时从悬置系统的角度出发,对悬置的刚度和安装位置进行优化,可以在不需改变发动机机械结构的情况下减少发动机传递给车身的不平衡激励。从图17和图18可以看出,悬置刚度和安装位置的优化对悬置在低转速下的受力情况有较为明显的改善。
4 结论
a) 在曲轴上加平衡重可以平衡曲柄活塞机构的旋转惯性力和部分一阶往复惯性力;在发动机上加平衡轴可以平衡部分一阶往复惯性力,平衡轴与曲轴上的平衡重配合使用,产生的附加力互相抵消,可实现完全平衡一阶往复运动惯性力;
b) 通过合理地布置悬置安装位置,调整悬置三向刚度,可以在不改变发动机机械结构的情况下,进一步优化悬置在发动机不平衡激励下的受力情况,减少发动机传递给车身的振动。
[1]SuhKH,LeeYK,YoonHS.Astudyonthebalancingofthethree-cylinderenginewithbalanceshaft[C].SAEPaper2000-01-0601.
[2]KarabulutH.Dynamicmodelofatwo-cylinderfour-strokeinternalcombustionengineandvibrationtreatment[J].InternationalJournalofEngineResearch,2012,13(6):616-627.
[3]KimC,KangYJ,LeeB,etal.Determinationofoptimalpositionforbothsupportbearingandunbalancemassofbalanceshaft[J].MechanismandMachineTheory,2012,50:150-158.
[4]ShangguanWen-Bin.Enginemountsandpowertrainmountingsystems:areview[J].InternationalJournalofVehicleDesign,2009,49(4):237-258.
[5] 上官文斌,黄天平,徐驰,等.汽车动力总成悬置系统振动控制设计计算方法研究[J].振动工程学报,2008,20(6):577-583.
[6]ShangguanWB,ZhaoY.Dynamicanalysisanddesigncalculationmethodsforpowertrainmountingsystems[J].InternationalJournalofAutomotiveTechnology,2007,(6):731-744.
[7] 陈大明.动力总成悬置系统刚体模态优化设计及位移计算方法[D].广州:华南理工大学, 2012.
[8]AkeiM,KouzatoK,UyamaT.StudyofEngineMountLayoutforIndustrialDiesel[C].SAEPaper2012-32-0108.
[9]TaoJS.DesignOptimizationofMarineEngine-mountsystem[J].JournalofSoundandVibration,2000,235 (3):477-494.
[10]AmbardekarMN,LogeshkumarN,GangurdePR,etal.VibrationIsolationofaPick-upVehiclewitha2-CylinderDieselEngine[C].SAEPaper2007-26-035.
[11] 徐石安.汽车发动机弹性支承隔振的解耦方法[J].汽车工程,1995,17(4):198-204.
[编辑: 李建新]
Balance Mechanism and Optimization of Mounting System of 2-Cylinder Engine
YU Liangwei1, SHANGGUAN Wenbin1, TANG Ying2, LI Jinting2
(1. School of Mechanical and Vehicle Engineering, South China University of Technology, Guangzhou 510641, China;2. SAIC-GM-Wuling Automobile Co., Ltd., Liuzhou 545007, China)
Taking a 2-cylinder engine as an object, the motion law of piston-crank mechanism was analyzed and the unbalanced forces and moments under actual operating condition were deduced. Then the balance method of rotating and reciprocating inertia forces for the 2-cylinder engine was researched and the impacts under different balance conditions were simulated. Moreover, the optimized model of mounting system for the 2-cyliner engine was built and the optimization of natural frequency, energy decoupling rate and mount dynamic reaction force were carried out with the sequence quadratic programming (SQP) method. The optimization of mounting system for the 2-cylinder engine shows that the method can reduce the engine excitation transferred to vehicle body effectively.
2-cylinder engine; balance mechanism; mounting system; multi-objective optimization
2015-03-17;
2015-05-25
余良渭(1991—),男,硕士,研究方向为汽车系统动力学;349733684@qq.com。
10.3969/j.issn.1001-2222.2015.06.001
TK421.5
B
1001-2222(2015)06-0001-07
