基于BSP－HAR－RV模型的最优抽样频率研究

李旭姣，张克勇

（中北大学，山西太原030051）

一、引 言

随着金融大数据时代的到来，我国金融市场也日益发展和完善，如何准确地测量和估计金融市场风险显得非常重要。近年，由于数据存储与处理技术的进步，获取高频数据更加容易。与传统的以日、月为频度记录的低频数据相比，高频数据中包含更全面的市场信息，有利于更加准确地估计波动率。由于从统计学的角度出发，处理高频数据非常困难，这方面的研究一直未能很好地进行。直到Anderson和Bollerslev（2011）［1］提出了已实现波动率（Realized Volatility，RV）这种能够较好度量高频数据波动变化的方法，掀起了学者们对高频数据研究的热潮。

Anderson等人在研究中不断对已实现波动率进行改进与完善，在对西方国家发达的金融市场高频数据研究过程中，发现已实现波动率具有显著的长记忆性和非对称性［2］，并将已实现波动率与条件协方差矩阵结合起来进行实证分析［3］，证明了已实现波动率的长记忆高峰VaR模型在波动率的预测上优于GARCH模型。基于Müller的异质市场假说理论，Corsi（2009）［4］提出了HAR－RV模型，通过日、月、周的已实现波动率的自回归过程，刻画市场交易者的异质性行为。后来，多位学者对该模型进行了多方面的扩展。在国内，徐正国和张世英（2004）［5］从调整的（已实现波动率）的长记忆性与杠杆效应的角度，建立了ARFIMAX模型，还将一维的高频数据RV模型扩展到多维的高频数据中。魏宇（2010）［6］利用沪深300股指期货的仿真交易数据，通过对股市波动预测模型的对比分析，得到ARFIMA－lnRV与SV－RV模型的预测能力都优于GARCH模型。张波等（2009）［7］用已实现波动率对沪指波动的相关特性进行实证研究，发现 HAR－RV模型比ARFIMA模型能更有效地刻画沪指波动的长记忆性，且其样本外预测能力也更强。陈浪南、杨科（2013）［8］构建了不对称性HAR－CJ－DFIGARCH模型，并对中国股市高频波动率进行了预测。

国内外对最优抽样频率的研究不多，一般都是基于“已实现”波动估计量的具体形式来进行的。最优抽样频率的选择方法大致可分为三种，波动率特征图法、利用日内收益序列相关性确定f和基于最小化MSE准则确定f［9］。Torben等学者（1999）［10］使用波动率特征图的方法，以平均已实现波动率和对应的频率描点，对最优频率进行选择。Bandi和Russell［11］在文中指出，应当首先建立已实现方差估计量的条件均方误差（MSE）表达式，作为采样频率的函数，再对采样频率选择的最低条件MSE进行优化。Christensen等人（2014）［12］在研究中指出，近年来，高频数据多使用五分钟作为采样频率，然而，在五分钟频率下，脉冲波动很容易被误认为是跳跃，使得人们对跳的普遍性存在产生误解。国外对高频数据抽样频率择优方面的研究越来越深入，方法也越来越精确，而国内对这方面的研究还停留在列举几个常见频率再进行对比选择的阶段，如李胜歌、张世英（2008）［13］采用列举法，以已实现波动率的均方误差作为标准对最优抽样频率的选择进行研究。这无形中就损失了很多有效信息，造成对波动率的估计不准确，进而无法更好地测量金融风险。本文首先以1到240分钟作横轴、以含跳的已实现平均波动率［14］作为纵轴描散点图，画出波动率特征图（BSP），结合均方误差MSE最小化，求出最优抽样频率（分钟）；再构建BSPHAR－RV模型，在最优频率下对高频数据时间序列波动率进行估计，并与常用的5min、10min抽样频率下的估计结果进行对比，验证结论。

二、BSP－HAR－RV模型

（一）HAR－RV模型

1．异质市场假说理论

异质市场假说理论（Muller，1993）指出，市场中存在不同类型的交易者，他们在风险偏好、信息获取、理性程度等各个方面存在着差异，这些差异的存在最终导致交易行为的差异。与传统的时间序列处理方法基于有效市场假说理论相比，已实现波动率模型基于异质市场假说，即不再把市场的参与者看成是同质的和理性的，而认为市场交易者存在差异，如小企业效应、季节效应等。

2．已实现波动率 （Realized Volatility，RV）

定义P（t）是金融资产在t时刻的价格，则在Δ时段上，金融资产的对数收益率可定义为：r（t，Δ）＝lnP（t，Δ）－lnP（t）。其中，Δ＞0表示时间间隔。例如，当Δ＝1时，r（t，1）＝lnP（t，1）－lnP（t）表示日间对数收益率。

在收益率均值为零的条件下，第t天的已实现波动率RV定义为：

其中，Δ是两次采样的时间间隔，1／Δ是采样频率。当Δ无限小趋于零时，即意味着取样是连续的，此时的已实现波动率收敛于积分波动率（Integrated

3．HAR－RV模型 （Heterogeneous Autoregressive model for Realized volatility，HAR－RV）

在异质市场假说框架下，HAR－RV模型将市场交易者分为短期交易者、中期交易者和长期交易者，短期交易不仅会受滞后期的影响，还会受同期中期交易的影响，中期交易也是如此。为了简便，分别把这三类交易者定义为日交易者、周交易者和月交易者。它们的已实现波动率定义如下（一周交易日为5天，一个月交易日为22天）：

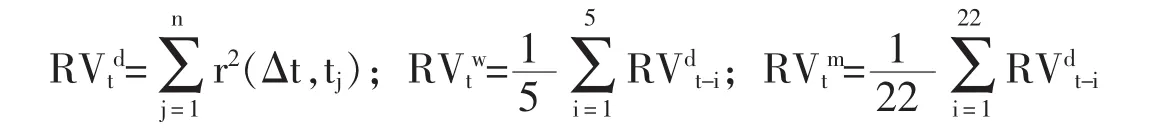
短期、中期和长期交易的已实现波动率如下：

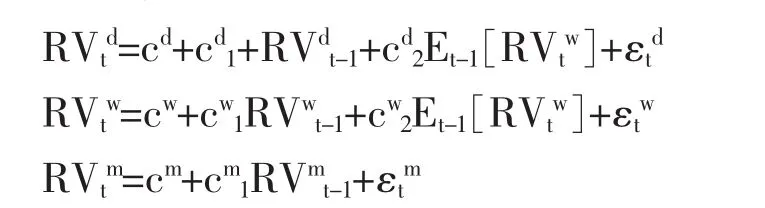
整理得到HAR－RV模型：

（二）BSP－HAR－RV模型

金融高频时间序列的精确性受到两种误差的干扰：测量误差和微观结构误差。因此，最优频率的选择至关重要，抽样频率越高，测量误差越小，微观结构误差越大。一方面，选择过高的抽样频率，可减小测量误差，却会导致市场微观结构误差的影响增大；别一方面，降低抽样频率，有效降低了微观结构误差的影响，却使测量误差成为主要干扰因素。最优频率的选择必须使得以上两类误差的总和取得平衡。另外，我国股市市场一天的交易时长为240分钟，于国外市场一天390分钟交易时长相比较短，所以我国的金融高频数据抽样频率取值范围要小，如果抽样频率取1分钟间隔以下的数值，对实际应用的价值不大，因此，取最短抽样间隔为1分钟，最大抽样频率为240分钟。选取收益率序列的双幂变差已实现波动率（BiPowe realized volatility）作为指标：

以抽样频率f（分钟）为横轴，以平均双幂变差已实现波动率为纵轴，作出平均双幂变差已实现波动率散点图（BiPowe realized volatility Signature Plot，BSP），并选取使得平均双幂变差已实现波动率序列的均方误差值（MSE）最小的频率作为最优抽样频率。

三、实证分析

（一）数据选取与整理

本文选择TCL集团2013年5月2日至2014年6月20日的每分钟股票价格作为样本，共有67035条记录，去除空值，得到TCL集团股票价格序列。

（二）数据基本统计特征分析

将TCL集团股票的价格序列进行对数化处理，得到对数收益率序列。从表1中可以看出，价格、成交量和收益率序列的偏度系数均不为0，峰度系数都大于3，这说明时间序列存在尖峰厚尾的现象。

表1 TCL集团股票价格、成交量、收益率的基本统计特征

（三）BSP－HAR－RV模型构建

1．最优频率的选择

为了得到更准确的波动率估计值，获得最优抽样频率是前提。作出TCL集团股票价格的平均含跳已实现波动率散点图 （BiPowe realized volatility Signature Plot，BSP）（如图1），通过R软件，得到不同频率下的平均含跳已实现波动率序列的均方误差值（MSE）序列的基本统计特征如图2。选取使得平均含跳已实现波动率序列的均方误差值 （MSE）最小的频率作为最优抽样频率，模型返回最优抽样频率为11分钟。

图1 TCL集团股票价格的波动率特征图

图2 均方误差值（MSE）序列的基本统计特征

2．BSP－HAR－RV模型预测分析和参数估计

用R软件的highfrequency软件包，对11分钟抽样频率下的对数收益率序列进行建模分析。在HAR－RV模型中，我们得到如下模型的参数估计结果：

RV1＝beta0＋beta1＊RV1＋beta2＊RV5＋beta3＊RV22

表2 BSP－HAR－RV模型预测分析和参数估计结果分析

模型预测拟合图如下：

图3 HAR－RV模型预测分析图

从图中可以直观地看出，在最优抽样频率下，BSP－HAR－RV模型能够较好地预测波动率趋势。其中，残差标准误差为0．0004895处于较低水平，每一个参数估计值都达到了99%以上的显著性水平。

3．BSP－HAR－RV模型比较分析

以往学者广泛采用5min和10min作为抽样时间间隔来获取高频数据，本文对选取了这两种频率下的时间序列进行模型估计，结果如下：

表3 5min抽样频率的模型参数估计结果

注：其中，残差标准误差为0．0005147；“＊＊＊”和“＊＊”分别代表显著性水平为0和0．001。

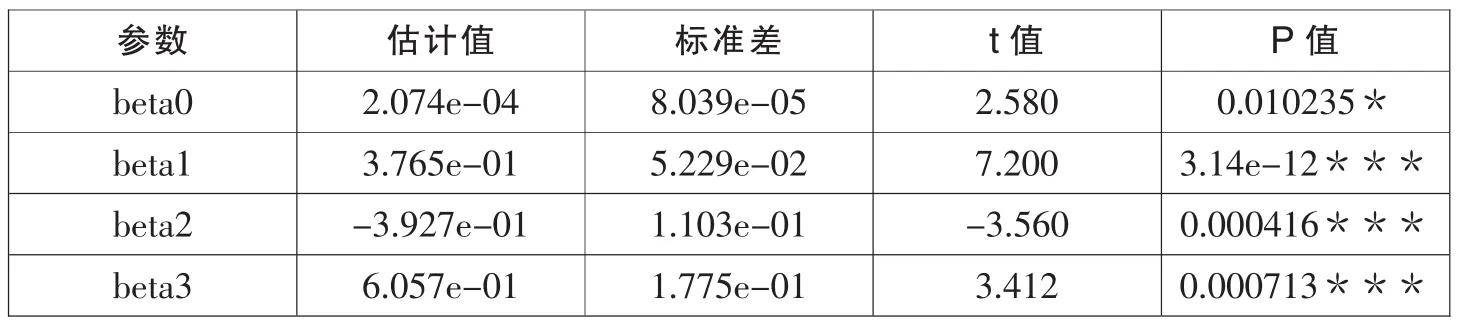
表4 10min抽样频率的模型参数估计结果

通过对比分析可得，5min抽样频率下，有参数beta2的P值为0．10043，大于 0．5，同时该抽样频率下的残差标准误差也高于最优频率11分钟下的残差标准误差；10min抽样频率下，虽然各个参数的显著性均符合要求，且相对来说比最优频率11分钟下的结果更好，但是其残差标准误差为0．0005662，更大。显然，BSP－HAR－RV模型在对抽样频率进行优化后得出了更精确的模型总体估计结果，具有可行性。

四、结束语

本文基于已实现波动率，充分考虑时间序列的长记忆性和市场交易的异质性，通过选择最优抽样频率，对HAR－RV模型进行优化。选取TCL集团个股进行实证分析，验证了模型的可行性。然而本文在选取样本的过程中，并未对不同特征（如流动性）的高频金融时间序列进行对比研究，无法确定BSP模型的适用条件，需要今后进一步研究。

［1］Andersen T G，Bollerslev T，Diebold F X，et al．The distribution of realized exchange rate volatility［J］．Journal of the American Statistical Association，2001，96：42－55．

［2］Andersen T G，Bollerslev T，et al．Exchange rate returns standardized by realized volatility are（nearly）gaussian［J］．Multinational Finance Journal，2000，（4）：159－179．

［3］ Andersen T G， Bollerslev T， Diebold F X， et al．Modeling and forecasting realized volatility［J］．Econometrica，2003，71（2）：579－625．

［4］Corsi F．A Simple Long Memory Model of Realized Volatility［R］．Journal of Financial Econometrics，2009，（7）：174－196．

［5］徐正国，张世英．调整“已实现波动率”与GARCH及SV模型对波动的预测能力的比较研究［J］．系统工程，2004，22（8）：60－63．

［6］魏宇．沪深300股指期货的波动率预测模型研究［J］．管理科学学报．2010，13（2）：66－76．

［7］张波，钟玉洁，田金方．基于高频数据的沪指波动的长记忆性驱动因素分析［J］．统计与信息论坛，2009，24（6）：21－26．

［8］陈浪南，杨科．中国股市高频波动率的特征、预测模型以及预测精度比较［J］．系统工程理论与实践，2013，33（2）：296－307．

［9］闵素芹，柳会珍．已实现波动率中最优抽样频率的选择［J］．理论新探，2009，（13）：13－15．

［10］Andersena T G，Bollerslevb T，Dieboldc F X，et al．Realized Volatility and Correlation［J］．1999．

［11］Bandi F M，Russell J R．Microstructure Noise，Realized Variance，and Optimal Sampling［J］．Review of Economic Studies，2008，（75）：339－369．

［12］Christensen K，Oomen R，Podolskij M．Fact or friction：Jumps at ultra high frequency［J］．Journal of Financial Economics，2014，114（3）：576－599．

［13］李胜歌，张世英．金融高频数据的最优抽样频率研究［J］．管理学报，2008，5（6）：801－840．

［14］Andersen T G，Dobrev D，Schaumburg E．Jump－robust volatility estimation using nearest neighbor truncation［J］．Journal of Econometrics，2012，169（1）：75－93．