各向异性半空间中浅埋孔洞对地表反平面运动的影响

陈志刚

1） 中国广州510632暨南大学力学与土木工程系 2） 中国广州510632暨南大学重大工程灾害与控制教育部重点实验室



各向异性半空间中浅埋孔洞对地表反平面运动的影响

1） 中国广州510632暨南大学力学与土木工程系 2） 中国广州510632暨南大学重大工程灾害与控制教育部重点实验室

本文采用复变函数方法研究了稳态水平剪切波（SH波）在各向异性弹性半空间中任意形状孔洞上的散射及其对地面运动的影响． 在变换空间中构造出自动满足各向异性半空间水平表面上应力为零的散射波函数， 并根据孔洞表面应力为零的边界条件， 采用最小二乘法求解散射波函数的系数． 用介质的各向异性性质来模拟地质条件， 给出了SH波作用下含圆孔、 椭圆孔和方孔的各向异性半空间表面位移幅值的数值结果， 并分析了介质特性、 孔洞的形状、 埋深、 入射波波数及入射角度等因素对地面运动的影响规律． 数值结果表明： 介质的各向异性对含有孔洞的半空间表面的地表位移具有显著的影响； 沿一定角度的入射波在某一频段内所引起的地表位移幅值比各向同性介质的可能要大, 且随着孔洞埋深的增加， 地表位移的幅值逐渐减小.

各向异性半空间 SH波散射 孔洞 地面运动 复变函数

Ji’nanUniversity,Guangzhou510632,China

引言

震害的调查和研究结果表明， 局部场地条件对地面运动有显著的影响（薄景山等, 2003； 景立平等， 2005）． 目前城市中修建了大量的地下结构物（如地铁、 隧道和管线等）， 当地震波与其发生相互作用时， 会导致地面运动局部的放大和空间变化的复杂性， 而这一现象的实质就是波的散射问题． 了解孔洞和隧道等地下结构物对弹性波的散射作用， 对进行建筑结构抗震设计和震害分析在工程上和理论上都具有重要意义．

求解弹性波在地下孔洞上的散射问题可采用解析方法和数值方法． 由于半空间中孔洞对弹性波散射的解析解答能够合理地解释地下结构对地面运动的影响， 因此这一问题的解析研究一直受到众多研究者的关注（田林等， 2012； 张家明等， 2012）． 在半空间中孔洞对弹性波散射的解析求解方面， 国内外研究者针对半空间介质为各向同性的情况作了大量的研究工作． 例如： Lee和Trifunac（1979）研究了各向同性半空间中圆形隧道对SH波的散射问题； 刘殿魁和林宏（2003）、 Wang和Liu（2002）采用复变函数和多极坐标法分别求解了半空间中圆孔和多圆孔对SH波的散射与地震动问题； Lee和Karl（1992）、 Davis等（2001）采用以大圆弧代替直边界的办法用傅里叶-贝塞尔级数展开法给出了半空间中圆形孔洞对SV波散射问题的解答； Liang等（2003）和梁建文等（2004）分别给出了SV波和P波作用下地下洞室群对地面运动影响问题的级数解．

在地震工程中常用的数值方法有: 有限差分法、 有限元法和边界元法. 由于边界元法可以方便地处理半无限介质中波的传播问题， 因此对弹性波在地下孔洞或隧道等结构物上散射问题的数值求解多采用这一方法． Manolis和Beskos（1988）用边界元法求解了半平面圆形洞室受SV波作用的动力响应； Luco和De Barros（1994）采用间接边界积分方程求解了SH波、 P波、 SV波和瑞雷波作用下含圆孔的黏弹性半空间表面的位移； 梁建文和巴振宁（2012）利用间接边界元法求解了层状半空间中洞室对平面SH波的放大作用； 梁建文等（2012， 2013）运用间接边界元法研究了弹性层状半空间中洞室对斜入射平面SH波的三维散射问题．

大部分岩土介质的物理力学性能均呈现出各向异性特征， 采用各向异性弹性半空间中孔洞模型能够更合理地描述实际地下结构物对地震波的传播和散射特性的影响， 获得更为可靠的地面运动影响的评价数据． 各向异性与各向同性介质中波的传播特性有着显著的不同， 这将会对地下孔洞或隧道等结构物引起的散射波产生影响. 各向异性介质中孔洞对地面运动产生的影响， 目前还缺乏足够的认识． 由于各向异性介质中波动方程的复杂性， 已有的关于弹性波在半空间中孔洞上的散射对地震动影响的解析研究大都针对各向同性介质的情况， 陈志刚（2012）研究了各向异性半空间中圆孔对SH波的散射所引起的圆孔附近的动应力集中问题． 本文将进一步研究各向异性半空间中非圆形柱状孔洞对平面SH波的散射问题， 主要考察介质的各向异性特性和孔洞的形状对地面运动的影响．

1 数学模型

本文所研究问题的数学模型如图1所示． 在各向异性弹性半空间中含有一个截面是任意形状的柱状孔洞， 其边界用S表示． 设该孔洞中心的轴线平行于弹性主方向z轴， 直角坐标系xoy位于柱状孔洞的横截面内， 与z轴垂直， 坐标原点o在孔洞横截面的中心上． 以水平表面为x1轴方向， 建立直角坐标系x1o1y1， 坐标原点o1位于孔洞中心点o的正上方， 两直角坐标系统的坐标原点之间的距离为h， 即孔洞的埋深．

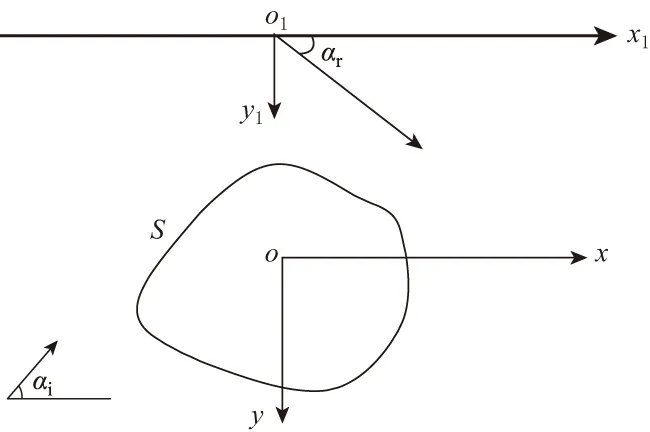
图1 SH波入射各向异性半空间中孔洞示意图

各向异性弹性介质中沿xoy平面入射和传播的平面SH波的控制方程在复平面z上可表示为（刘殿魁， 1988）

（1）

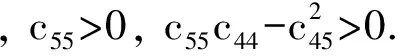
对于图1所示的SH波散射问题， 引入映射函数z=ω（ζ）， 再引入坐标变换

（2）

（3）

考虑稳态的平面SH波，w（i）在xoy平面内， 与x轴成αi角度入射, 其在水平表面o1x1时将产生反射的SH波w（r）． 在省略时间因子e-iωt的情况下（以下散射波也相同）， 入射波w（i）和反射波w（r）在映射平面ζ上可以分别表示为

（4）

（5）

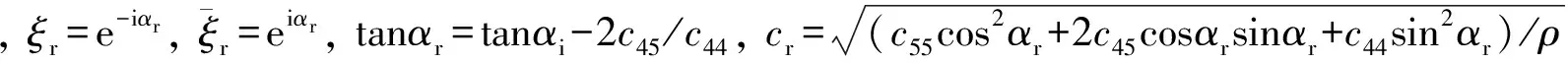
引入映射函数z=ω（ζ）和变换式（2）后， 在极坐标系中应力和位移关系的表达式分别为

{[（c55-c44+i2c45）（1-iγ）+（c44+c55）

（6）

（7）

2 分析求解

对于各向异性弹性半空间中孔洞在SH波作用下引起的散射波， 在复平面z上为

（8）

将散射波函数式（8）代入式（7）求解散射波引起的应力. 当θ=0或π时， 该应力为零， 说明孔洞引起的散射波在半空间表面上产生的应力为零， 可根据孔洞的边界条件直接求得式（8）所表示的散射波函数的系数An．

在含有孔洞的各向异性弹性半空间中， 由SH波产生的总波场w（t）可表示为

w（t）=w（i）+w（r）+w（s）,

（9）

式中，w（s）为入射波w（i）和反射波w（r）在半空间中孔洞上所产生的散射波， 其形式如式（8）所示， 能够自动满足边界x1轴上应力为零的条件．

各向异性半空间中孔洞表面上满足应力为零的边界条件， 在复平面z上表示为

（10）

将式（4）、 （5）和（8）分别代入式（6）， 求得相应的应力， 则边界条件式（10）可表示为

（11）

其中，

用最小二乘法求解式（8）中的散射波系数An：

（12）

对散射波函数取有限项， 根据边界条件式（11）可得到一组超定线性方程组， 由式（12）可求解该方程组， 求得未知系数An， 项数n的选取受求解精度的控制．

3 计算结果

本文的计算结果给出了各向异性半空间中圆孔、 椭圆孔和方孔在SH波作用下的地表位移． 在式（9）的计算中， 需代入映射函数ω（ζ）的具体形式（陈志刚， 2007）． 为了综合考虑地表位移与孔洞的几何特征和入射波频率的关系， 采用无量纲化的地表位移幅值和入射波频率． 水平地表面上的无量纲位移幅值wd为

（13）

无量纲频率η定义为

（14）

式中： a为孔洞的几何特征尺寸， 在本文中分别表示圆孔的半径、 椭圆孔的长半轴和正方形孔边长的一半； λ为入射波波长．

图2给出了各向同性、 正交各向异性和各向异性半空间中浅埋圆孔在不同频率的SH波作用下， 圆孔上方的地表位移幅值wd的变化曲线． 图中， β1=c45/c55， β2=c44/c55, α0为

图2 介质参数变化对浅埋圆孔附近地表位移幅值的影响

入射角． 在埋深h与圆孔半径a比值为1.5的情况下， 由于孔洞的存在， 半空间地表位移会发生很大的变化， 且当入射波频率较高时， 这种影响会更加显著． 在SH波垂直入射时， 各向同性介质与正交各向异性介质的地表位移是对称的， 而各向异性介质（c45≠0）的地表位移则不再对称． 同时， 介质的各向异性性质对地表位移会产生明显的影响. 当β2=0.5时, 其水平方向的剪切模量与竖向的剪切模量相差一倍， 当SH波垂直入射， 且频率较低时（η=0.1）（图2a）， 圆孔正上方的地表位移比无孔时要大， 与各向同性介质情况相比， 各向异性介质中在孔洞正上方点的地表位移要低些； 当β2=1.5时， 各向异性半空间中圆孔上方地表位移比各向同性介质中的要高些． 当频率较低（η=0.1）的SH波沿水平方向入射， β2=0.5时, 圆孔上方地表位移比各向同性介质的要大； 当β2=1.5时， 圆孔上方地表位移比各向同性介质的要小． 这说明各向异性介质的特性对地表位移的影响与入射波方向密切相关． 但随着入射波频率的增加， 当SH波垂直入射时， 无论介质性质如何， 圆孔正上方地表位移的幅值都明显降低， 而圆孔两侧地表位移则发生剧烈变化． 与无孔半空间相比， 此时地表位移幅值明显增大． 介质的各向异性对地表位移幅值的影响与入射波的频率相关． 从图2c可以看出， 当SH波垂直入射时， 各向异性介质中圆孔两侧上方的地表位移幅值与各向同性介质相比有明显提高， 地表位移最大的幅值wd=2.93， 是各向同性介质的1.12倍． 当频率η=2.0时， 介质的各向异性对地表位移的影响不明显．

当SH波沿水平或倾斜方向入射时， 从图2的地表位移的幅值曲线可以看出： 在迎波面一侧位移的幅值曲线波动很大， 而且随着入射波频率的增加， 地表位移的这种波动变化更加显著； 而在圆孔的背波面一侧地表位移的幅值则明显低于迎波面一侧， 且圆孔后面各点地表位移幅值变化的震荡性显著降低. 说明孔洞的存在对这一区域起到了屏蔽作用， 但这种屏蔽作用随着入射波频率的增加会有所减弱． 介质的各向异性对地表位移会产生较大的影响， 当SH波沿水平方向入射， β2=0.5时， 在低频段（η=0.1）的地表位移wd=3.06， 与各向同性介质相比， 地表位移的幅值提高了12%； 当η=1.0时， 地表位移wd=4.54， 与各向同性介质相比， 地表位移的幅值提高了17%； 当η=2.0时， 介质的各向异性对地表位移的影响不显著（图2d）．

图3给出了入射SH波频率在η=0.1-2.0之间、 埋深h与圆孔半径a之比为1.5、 波垂直或水平入射时， 含圆孔的正交各向异性（β1=0, β2=0.5）半空间地表位移的幅值曲线． 可以看出， 地表位移幅值的大小与入射波频率密切相关， 在一定频段内孔洞对地表位移的影响比较明显， 而在另一频段则对地表位移的影响会减弱． 应充分考虑各种因素的影响．

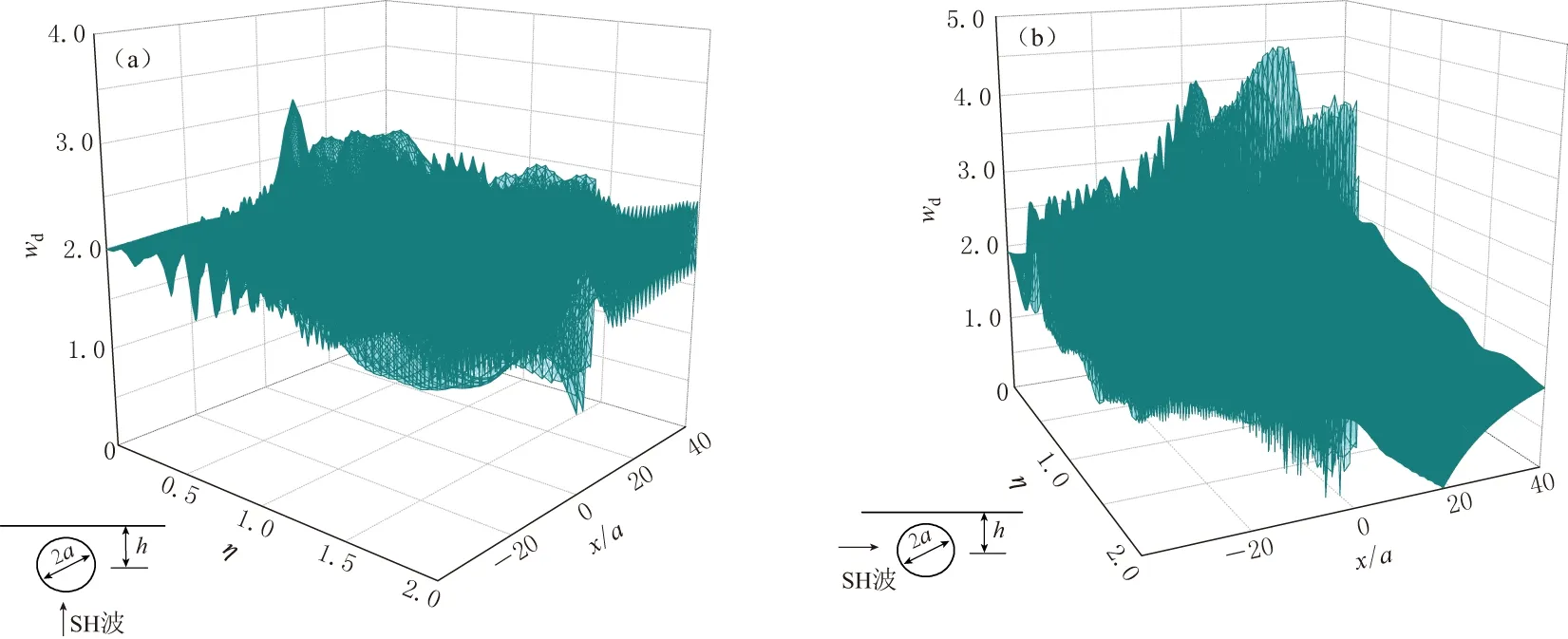
图3 含圆孔正交各向异性半空间表面位移随频率的变化

图4给出了SH波入射不同埋深圆孔时， 正交各向异性（β1=0, β2=0.5）半空间表面上的位移幅值曲线． 可以看出， 无论SH波是水平入射还是垂直入射， 地表位移的幅值随孔洞埋深的增加总体上是减弱的， 但究竟孔洞埋深多少时可以不考虑其作用， 还需考虑多种因素来确定． 比较不同频率与埋深下地表位移幅值的变化曲线可以看出， 当波高频入射时， 地表位移幅值衰减得慢． 由图4a可以看出， 在不同埋深情况下， 当SH波以不同波数沿水平方向入射时， 地表位移幅值均表现出在迎波面的一侧变化剧烈， 而在孔后面地表位移变化则比较平缓． 在相同波数和埋深情况下， 与各向同性介质半空间中的圆孔情况相比（刘殿魁, 林宏, 2003）， 地表位移幅值有了显著的提高（图4a）． 在SH波垂直入射下， 当h/a>12时， 随着孔洞埋深的增加， 地表位移幅值已变化不大（图4b）. 但当入射波频率较高时， 随着孔洞埋深的增加， 孔洞的影响则消除得很慢． 而当波沿水平方向入射时， 孔洞对地表位移幅值影响的消除要比垂直入射时的还要更慢些．

图4 正交各向异性半空间圆孔埋深对地表位移幅值的影响

图5给出了当半空间中埋深与椭圆长轴之比为1.5时， 不同频率SH波作用下， 浅埋椭圆孔上方地表位移幅值的变化曲线． 图中将各向同性（β1=0, β2=1.0）、 正交各向异性（β1=0, β2≠1.0）和各向异性（β1≠0, β2≠1.0）的情况作了对比． 与图2中相同埋深和介质参数下浅埋圆孔情况相比， 当SH波的入射方向垂直于椭圆的长轴时， 波的散射作用所引起椭圆孔上方地表位移的变化更为剧烈； 而当SH波水平入射时， 这时入射波沿x轴方向传播， 与椭圆长轴方向一致， 浅埋椭圆孔所引起的地表位移要比圆孔时的小一些． 数值结果表明， 地表位移幅值大小与孔洞形状、 入射波方向、 入射波频率和介质各向异性等因素密切相关． 与浅埋圆孔情况类似， 在某一参数组合下， 各向异性半空间中的椭圆孔能够在地表面局部引起较高的位移． 在介质参数β1=0.2、 β2=0.5情况下， 当SH波以频率η=0.5倾斜入射时， 椭圆孔上方的地表位移wd=3.02， 与相同情况下各向同性介质中椭圆孔相比， 其地表位移的幅值提高了29%．

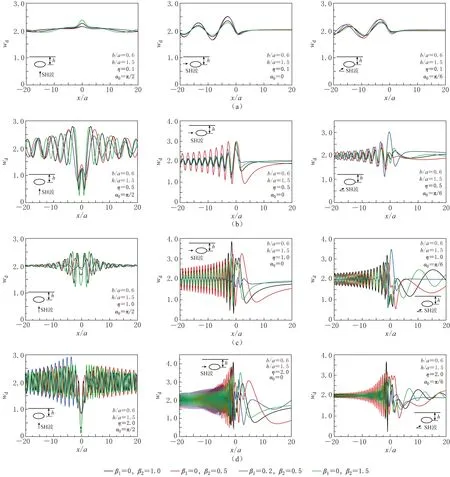
图5 介质参数变化对浅埋椭圆孔附近地表位移幅值的影响

图6给出了当埋深与方孔边长一半之比为1.5时， 在不同频率SH波作用下， 浅埋方孔上方地表位移幅值的变化曲线． 可以看出， 地表位移随介质参数、 入射波频率和入射方向的变化规律与浅埋圆孔和浅埋椭圆孔的情况相似， 但由于孔洞形状引起的散射效应不同， 各向异性半空间中浅埋方孔能引起更大的地表位移． 在介质参数为β1=0.2、 β2=0.5情况下， 当SH波以频率η=0.5倾斜入射时， 方孔上方的地表位移wd=3.67， 与相同情况下各向同性介质中方孔相比， 其地表位移幅值提高了36%．

图6 介质参数变化对浅埋方孔附近地表位移幅值的影响

4 讨论与结论

本文采用复变函数方法构造了SH波作用下各向异性弹性半空间中孔洞的散射波函数， 该散射波在各向异性半空间表面上引起的应力为零， 得到了含有孔洞的各向异性半空间表面位移的解析解， 并分析了半空间中存在孔洞时， 介质特性、 埋深和入射波数等因素对地表位移幅值的影响， 得到如下结论：

1） 在含有孔洞的各向异性半空间中， 沿某一方向的入射波有可能引起地表位移幅值显著增大的现象， 而地表位移变化的幅度与介质的各向异性强度和方向有很大关系， 同时还受到入射波方向、 频率和孔洞形状的影响．

2） 半空间中孔洞对地表位移有显著影响， 在各向异性介质中这种影响有时比各向同性介质要大得多. 随着孔洞埋深的增加， 孔洞的影响逐渐减弱， 但在较高频率的SH波作用下， 地表位移的幅值随孔洞埋深的增大而缓慢地减小．

3） 当孔洞埋深较浅时， 孔洞引起的散射波对地表位移影响很大， 在孔洞上面一定范围内地表位移会出现急剧增加的现象， 因此在地下结构物或有埋藏物的上方修建建筑物时， 要充分考虑其对场地地面运动的影响．

研究各向异性介质中波在地下结构上的散射问题在地震工程中具有重要意义. 本文研究的是这一问题中最简单的模型， 给出了介质的各向异性对地面运动影响的初步解释. 进一步的研究有待于各向异性半空间中孔洞对P波和SV波散射的求解， 以及各向异性介质中的弹性波在地下孔洞上三维散射问题的解答．

薄景山, 李秀领, 李山有. 2003. 场地条件对地震动影响研究的若干进展[J]. 世界地震工程, 19（2）: 11--15.

BoJS,LiXL,LiSY. 2003.Someprogressofstudyontheeffectofsiteconditionsongroundmotion[J]. World Earthquake Engineering, 19（2）: 11--15 （inChinese）.

陈志刚. 2007. 浅埋孔洞对地表反平面运动的影响[J]. 岩土力学, 28（8）: 1655--1660.

ChenZG. 2007.Effectsofshallowburiedcavityonanti-planegroundmotion[J]. Rock and Soil Mechanics, 28（8）: 1655--1660 （inChinese）.

陈志刚. 2012.SH波作用下各向异性弹性半空间中浅埋圆孔附近的动应力集中研究[J]. 岩土力学, 33（3）: 899--905.

ChenZG. 2012.DynamicstressconcentrationaroundshallowcylindricalcavitybySHwaveinanisotropicallyelastichalf-space[J]. Rock and Soil Mechanics, 33（3）: 899--905 （inChinese）.

景立平, 卓旭炀, 王祥建. 2005. 复杂场地对地震波传播的影响[J]. 地震工程与工程振动, 25（6）: 16--23.

JingLP,ZhuoXY,WangXJ. 2005.Effectofcomplexsiteonseismicwavepropagation[J]. Journal of Earthquake Engineering and Engineering Vibration, 25（6）: 16--23 （inChinese）.

梁建文, 张浩,LeeVW. 2004. 地下洞室群对地面运动影响问题的级数解答：P波入射[J]. 地震学报, 26（3）: 269--280.

LiangJW,ZhangH,LeeVW. 2004.Aseriessolutionforsurfacemotionamplificationduetoundergroundgroupcavities:IncidentPwaves[J]. Acta Seismologica Sinica, 26（3）: 269--280 （inChinese）.

梁建文, 巴振宁. 2012. 层状半空间中洞室对平面SH波的放大作用[J]. 地震工程与工程振动, 32（2）: 14--24.

LiangJW,BaZN. 2012.AmplificationofplaneSHwavesbyacavityinlayeredhalf-space[J]. Journal of Earthquake Engineering and Engineering Vibration, 32（2）: 14--24 （inChinese）.

梁建文, 陈健琦, 巴振宁. 2012. 弹性层状半空间中无限长洞室对斜入射平面SH波的三维散射（Ⅰ）： 方法及验证[J]. 地震学报, 34（6）: 785--792.

LiangJW,ChenJQ,BaZN. 2012. 3DscatteringofobliquelyincidentSHwavebyacylindricalcavityinlayeredelastichalf-space（Ⅰ）:Methodologyandverification[J]. Acta Seismologica Sinica, 34（6）: 785--792 （inChinese）.

梁建文, 陈健琦, 巴振宁. 2013. 弹性层状半空间中无限长洞室对斜入射平面SH波的三维散射（Ⅱ）： 数值结果与分析[J]. 地震学报, 35（2）: 173--183.

LiangJW,ChenJQ,BaZN. 2013. 3DscatteringofobliquelyincidentSHwavebyacylindricalcavityinlayeredelastichalf-space（Ⅱ）:Numericalresultsandanalysis[J]. Acta Seismologica Sinica, 35（2）: 173--183 （inChinese）.

刘殿魁. 1988. 各向异性介质中SH波引起的圆孔附近的动应力集中[J]. 力学学报, 20（5）: 443--452.

LiuDK. 1988.DynamicstressconcentrationaroundacircularcavitybySHwaveinananisotropicmedia[J]. Acta Mechanica Sinica, 20（5）: 443--452 （inChinese）.

刘殿魁, 林宏. 2003. 浅埋的圆柱形孔洞对SH波的散射与地震动[J]. 爆炸与冲击, 23（1）: 6--12.

LiuDK,LinH. 2003.ScatteringofSHwavesbyashallowburiedcylindricalcavityandthegroundmotion[J]. Explosion and Shock Waves, 23（1）: 6--12 （inChinese）.

田林, 徐则民, 张家明. 2012. 局部地形下入射波散射效应对场地地震响应的影响[J]. 地球物理学进展, 27（1）: 122--130.

TianL,XuZM,ZhangJM. 2012.Seismicresponseforlocallandformsubjectedtoscatteringofincidentwave[J]. Progress in Geophysics, 27（1）: 122--130 （inChinese）.

张家明, 徐则民, 田林, 裴银鸽. 2012. 局部地形下入射波散射效应对地震动影响解析解研究进展[J]. 中国地震, 28（3）: 231--244.

ZhangJM,XuZM,TianL,PeiYG. 2012.Areviewofanalyticalsolutionofscatteringeffectofincidentwavebylocaltopographyongroundmotion[J]. Earthquake Research in China, 28（3）: 231--244 （inChinese）.

DavisCA,LeeVW,BardetJP. 2001.TransverseresponseofundergroundcavitiesandpipestoincidentSVwaves[J]. Eng Struct Dyn, 30（3）: 383--410.

LeeVW,TrifunacMD. 1979.ResponseoftunnelstoincidentSH-waves[J]. Eng Mech Div ASCE, 105（4）: 643--659.

LeeVW,KarlJ. 1992.DiffractionofSVwavesbyundergroundcircularcylindricalcavities[J]. Soil Dyn Earthq Eng, 11（8）: 445--456.

LiangJW,ZhangH,LeeVW. 2003.Aseriessolutionforsurfacemotionamplificationduetoundergroundtwintunnels:IncidentSVwaves[J]. Earthquake Engineering and Engineering Vibration, 2（2）: 289--298.

LucoJE,DeBarrosFCP. 1994.Dynamicdisplacementsandstressesinthevicinityofacylindricalcavityembeddedinahalf-space[J]. Earthq Eng Struct Dyn, 23（3）: 321--340.

ManolisGD,BeskosDE. 1988. Boundary Element Methods in Elastodynamics[M].London:Unwin-Hyman： 83--115.

WangGQ,LiuDK. 2002.ScatteringofSHwavebymultiplecircularcavitiesinhalfspace[J]. Earthquake Engineering and Engineering Vibration, 1（1）: 36--44.

Effect of shallow buried cavity on anti-plane motion of ground surface in anisotropic half-space

1）DepartmentofMechanicsandCivilEngineering,Ji’nanUniversity,Guangzhou510632,China

2）KeyLaboratoryofDisasterForecastandControlinEngineering,MinistryofEducation,

The scattering of steady-state horizontal shear wave （SH-wave） by arbitrary cavity in anisotropic half-space is investigated together with its effect on ground motion by using the complex variable function method. The scattered wave function stratifying the condition of the stress free on the horizontal surface of anisotropic-half space automatically is constructed in the transformed space. Based on the zero-stress boundary condition of the cavity surface, the coefficient of scattered wave function is solved by means of the least squares method. By simulating the geological condition of the media anisotropy, the ground surface displacement amplitudes of anisotropic half-space with circular cavity, elliptical cavity and quadrate cavity are illustrated numerically. The effect of ground motion on the media property, the cavity shape, buried depth, the wave number and incident angle of incident wave are analyzed. Numerical result shows the media anisotropy has great effects on the ground surface displacement of half-space with a cavity. The ground surface displacement amplitude caused by incident wave with a certain angle may be much greater than that of the isotropic media in a certain frequency range, and decreases with the increase of the cavity depth.

anisotropic half-space; scattering of SH wave; cavity; ground motion; complex variable function

10.11939/jass.2015.04.008.

教育部重点实验室项目“重大工程灾害与控制”和广东省高等学校科研型重点实验室项目“工程结构故障诊断”共同资助.

2014-08-11收到初稿， 2015-01-24决定采用修改稿.

e-mail: czgjnu@163.com

4.008

P315.9

A

陈志刚. 2015. 各向异性半空间中浅埋孔洞对地表反平面运动的影响. 地震学报, 37（4）: 617--628.

Chen Z G. 2015. Effect of shallow buried cavity on anti-plane motion of ground surface in anisotropic half-space.ActaSeismologicaSinica, 37（4）: 617--628.

doi:10.11939/jass.2015.04.008.