川滇菱形地块的应变能积累释放周期和强震预测

许昭永 文丽敏 石宝文 许 峻樊俊屹 李正媛 苏有锦

1） 中国昆明650091昆明南方地球物理技术开发有限公司2） 中国昆明650091云南大学资源环境与地球科学学院 3） 中国北京100045中国地震台网中心 4） 中国昆明650224云南省地震局



川滇菱形地块的应变能积累释放周期和强震预测

1） 中国昆明650091昆明南方地球物理技术开发有限公司2） 中国昆明650091云南大学资源环境与地球科学学院 3） 中国北京100045中国地震台网中心 4） 中国昆明650224云南省地震局

将川滇菱形地块分为两个地块， 分别以形变确定应变速率、 深部速度构造确定弹性模量、 联合地块体积确定地块应变能积累与时间的关系， 结合历史强震研究应变能积累释放周期以及该周期内的强震活动， 进而研究应变能积累释放与强震活动的关系． 结果表明， 地块应变能积累释放存在周期性并可预测强震震级． 在应变能积累前期， 没有强震（M≥7.0）发生； 随着时间增加， 应变能继续增加， 地块上先后发生几次强震， 但每次强震震级均小于预测震级， 即一次强震只释放了一部分能量； 而后应变能积累继续增加， 直到一、 二次特大强震（M≥7.5）发生， 将绝大部分应变能释放. 至此， 老的周期结束， 新的周期开始． 应变能积累从小到大直到最后完全释放的周期性导致了地震的平静活跃周期， 地震活跃期比平静期长得多． 本文认为， 大区域地理范围因其含有多个地块， 不宜讨论其地震平静活跃周期， 而对于小范围单次强震也不宜讨论其复发周期． 虽然活跃期中的强震从时间上看并无任何规律， 但利用活动地块应变能的积累释放曲线所预测的震级与实际震级很接近． 本文结果对于地震安全性评价工作可能有重要意义．

活动地块 应变能 积累释放周期 强震活动 地震预测

引言

地震学家早已注意到地震轮回（旋回）现象， 并且研究这种轮回是否存在周期性（许绍燮， 1982； 张国民等， 1993）． 诸多研究人员对同一地区原地重复发生强震的周期性以及一些典型的强震前后地壳变形轮回的周期性进行了研究（Shimazaki， 1976； Thatcher， 1983； 蔡静观, 刘正荣, 1990; Scholz， 1996; 皇甫岗等, 2010）． 另外， 对地震危险性进行分析时通常针对一个很大（但确定）的地理范围， 讨论地震的平静期和活跃期等． 这两者虽然差异明显， 一个范围很小， 一个范围很大， 但都存在明显不足： 强震原地重复发生只考虑单一孕震区状态可能漏掉其它信息， 大范围地震危险性分析包含多个地块可能使多种信息互相抵消； 两者均未将一个完整地质单元体（如活动地块）作为研究对象， 研究其构造特征、 应力、 变形历史及现状等， 因此并未充分涉及其内在的物理意义． Wang 等（2006）用岩石试验研究地震复发周期， 但并未研究地块应变能积累释放周期对地震活动规律的影响； 陈祖安等（2009）研究了中国西南地区应变能密度分布特征及汶川MS8.0地震孕震机理， 但并未研究地块总应变能积累对强震震级的影响； 许昭永等（2010）初步研究利用地块应变能预测潜在地震危险区及其最大震级， 但有许多问题还需进一步研究． 本文将依据张培震等（2003）提出的活动地块或新构造划分的地质地块、 大地测量资料、 深部速度结构等计算地块应变能积累， 并依据历史强震资料分析整个地块应变能积累释放周期与地震活动性特征的关系， 包括平静活跃循环周期和震级预测等， 同时对相邻地块的相互影响作出讨论．

1 地块应变能积累

地块应变能（积累）计算式（尹祥础， 2011）为

W=∬w（x,y,z;t）dvdt,

（1）

式中，w（x,y,z;t）为应变能密度， 其与所在位置及时间有关． 应变能W的大小还与地块积聚体积及时间长短有关．

1.1 完整地块应变能密度

对于线弹性体， 其应变能密度为

（2）

广义胡克定律为

σij=2μεij+λϑδij,

（3）

式中:λ为拉梅常数；μ为剪切模量； ϑ为应变；σij和εij分别为应力分量和应变分量； 当i=j时，δij=1； 当i≠j时，δij=0．

当测得3个方向的主应变， 其它6个（3对）剪应变都取最大值时， 可导出下式：

）.

（4）

1.2 应变能积累零点（基值）或起始时间的确定

要确定积累了多少应变能或应变能零点甚难． 经过对比研究， 本文建议取某次特大地震（M≥7.5）的发生时间为后续应变能积累的起始时间． 若这一时期连续发生两次M≥7.5强震， 则取后一次强震为后续应变能积累周期的起始时间， 以确保新的周期开始后其前一周期的应变能绝大部分（或完全）已释放， 并假定起始时的应力、 应变或应变能基点（基值）为零． 当然， 这并非真正零点， 还包含有一定程度的应力、 应变（或应变能）， 其大体为常数． 基点的物理意义为， 当应力、 应变或应变能低于这个基值时， 不会有强震发生， 只有高出这个基值很多才可能引发强震．

1.3 年平均应变率的测定

用应力、 应变测量结果估算应变能密度比较直接， 但现今应力测量依然较难． 而以GPS实测地形变（应变）则很容易进行， 所以常用应变及弹性常数确定应力． 然而对大多数地块而言， 形变观测历史甚短， 只能对应力和应变分别取平均（或应力速率和应变速率）， 并且假定应力速率与应变速率为线性关系， 即

（5）

由于假设基值应力和应变均为零， 故在时间T后， 应力与应变关系为

ϑδij.

（6）

从式（2）、 （3）及（6）导出下式：

j.

（7）

张培震等（2008）和许昭永等（2010）的研究结果表明， 由地震地质方法所得结果与GPS实测结果非常接近． 因此， 地块应变速率一般应由GPS测定， 在资料缺乏时， 也可由地质资料推测．

1.4 弹性常数的确定

岩体弹性模量在地表由静载荷试验直接测定， 但在地壳深部则无法进行． 高温高压岩样试验结果有限， 很难区分地区差异． 故取地壳的纵、 横波速度和密度估测弹性常数， 进而估算应变能密度的平均值． 由下式计算λ和μ， 进而可得出泊松比ν和弹性模量E等其它弹性常数：

（8）

式中ρ为密度． 随着深度增加， （围）压力升高、 温度增加． 前者使岩体强度增加， 后者使岩体强度降低． 参照周永胜和何昌荣（2009）的研究结果， 大约在25 km深度附近， 岩体强度最高． 对巨大压力能起决定作用的正是该层， 故本文取25 km深度附近的波速来确定其弹性常数．

1.5 地块体积及应变能的确定

对于大的地块， 本文采用张培震等（2003）关于活动地块的定义和方法进行划分； 对于相对小一些的地块， 采用地震安全性评价中的Ⅱ和Ⅲ级构造划分地块． 这种地块不宜太小， 其边界应有明确的界限特征， 地块内部可能还存在并未贯穿整个地块的断层． 地块底面以地壳底面为界， 由此估测地块积累应变能的体积．

对于地块应变能的计算， 本文以一整个地块估算其应变能． 由式（1）导出下式：

（9）

对于地块应变能的计算， 可将其分成许多小地块（有限单元体）， 并假定应变能密度均匀分布， 而后将所有小地块叠加得出地块总应变能． 也可以将各个小地块应变能密度按体积比加权平均， 当各个小地块体积相等时， 则所有小地块的应变能密度平均值即为地块平均应变能密度． 由于观测点有限且偏少， 所以我们取地块应变能密度平均值和体积计算其总应变能． 对于含有断层或由几部分组成的地块， 可先将其划分为几个地块分别进行计算， 而后叠加， 求出总应变能．

2 强震震级预测

研究结果表明（Kanamori， 2001）， 地震效率（一次地震释放的应变能占积累的总应变能的百分比）大约为百分之几到百分之十几， 其上限为18%． 本文取地震效率为15%， 依据震级-能量关系（Gutenberg， Richter， 1942）估算震级：

（10）

由于到某次强震发生时， 块体应变能并非单调增长， 而是此前发生的强震已释放了部分应变能． 其实际应变能积累为

（11）

式中：Wts为到t时刻的地块应变能积累， 可由式（2）， （3）， （7）， （9）计算出；Wti为t时刻之前各次强震所释放的应变能， 由式（10）计算． 此时可由式（11）所得到的能量通过式（10）预测未来发生最大强震的震级．

3 资料处理及实例分析

强震前会出现一系列地形变方面的特征变化， 一般发生在应变集中区或高应变梯度区． 利用形变场的空间特征判定强震发生位置是可行的． 此外， 利用地震活动性方法和地震地质方法确定地震危险区也是可行的, 这里不再赘述． 本文以川滇菱形地块为例， 说明如何利用应变能积累释放周期预测强震活动．

3.1 川滇菱形地块的体积

川滇菱形地块被羌塘、 巴颜喀拉、 华南、 滇南和滇西地块所包围， 如图1所示（张培震等， 2003； 皇甫岗等， 2010）. 其面积约为26万 km2． 皇甫岗等（2010）以丽江—小金河断裂带为界， 参照地壳厚度将川滇菱形地块再划分为两块： 西北地块和东南地块． 如图2所示， 川滇地区地壳厚度北厚南薄， 在丽江—小金河断裂带附近厚度梯度变化较大． 该断裂带的西北地块地壳厚度较大， 为48—64 km， 平均为56 km； 东南地块厚度较小， 为38—48 km， 平均为43 km． 西北地块面积约为1.51×1011m2， 体积约为8.46×1015m3； 东南地块面积约为1.16×1011m2， 体积约为4.99 ×1015m3．

3.2 川滇菱形地块的弹性常数

根据王椿槦等（2003）关于30°N线地壳上地幔P波速度结构剖面， 在深度25—30 km处， 龙门山断裂带东侧纵波速度vP=6.35 km/s， 西侧及鲜水河断裂带以西vP=6.25 km/s， 密度均为ρ=2.70×103kg/m3． 根据刘启元等（2009）关于31°N线地壳上地幔S波速度结构剖面， 在深度25—30 km处， 龙门山断裂带东侧和鲜水河断裂带西侧横波速度均为vS=3.85 km/s， 两断裂带之间vS=3.60 km/s． 龙门山断裂带东侧（成都地块）剪切模量μ=4.002×1010Pa， 泊松比ν=0.209； 两断裂带之间（巴颜喀拉地块）μ=3.499×1010Pa，ν=0.252． 川滇西北地块的弹性参数与鲜水河断裂带西侧相同， 即μ=4.002×1010Pa，ν=0.194，λ=2.537×1010Pa．

黄永祥等（2002）利用滇中地壳的速度结构， 计算出川滇东南地块中小江断裂带区域、红河断裂带区域及两断裂带中间区域的弹性模量分别为6.98×1010Pa， 2.80×1010Pa和7.74×1010Pa． 其中弹性模量较低区域位于断裂带附近， 而地块内部弹性模量则较高． 本文取川滇东南地块的弹性模量E=7.74×1010Pa， 剪切模量μ=3.173×1010Pa， 泊松比ν=0.220， 拉梅常数λ=2.493×1010Pa．

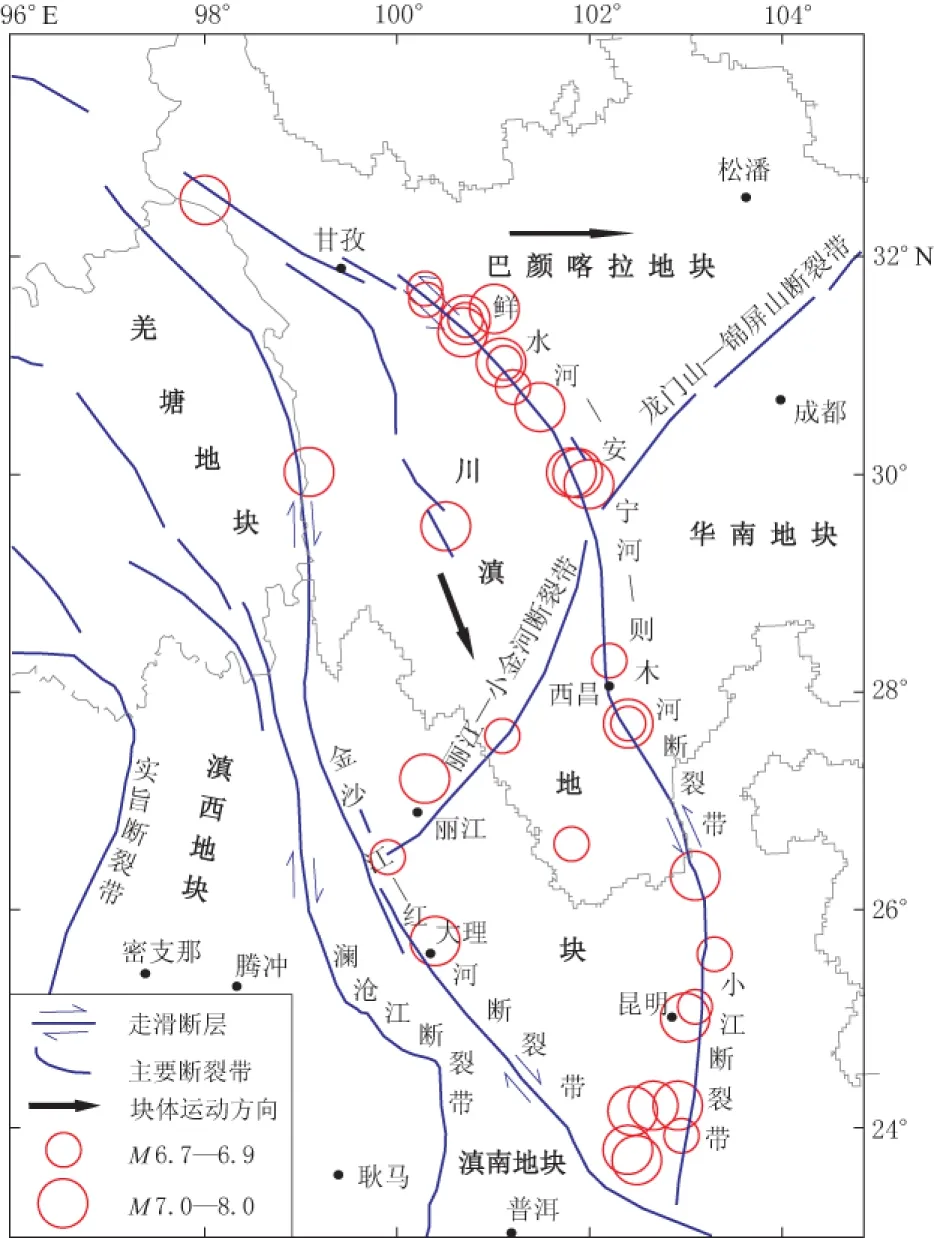
图1 川滇菱形地块地质构造图及1700年以来M≥6.7强震分布图（引自皇甫岗等， 2010）

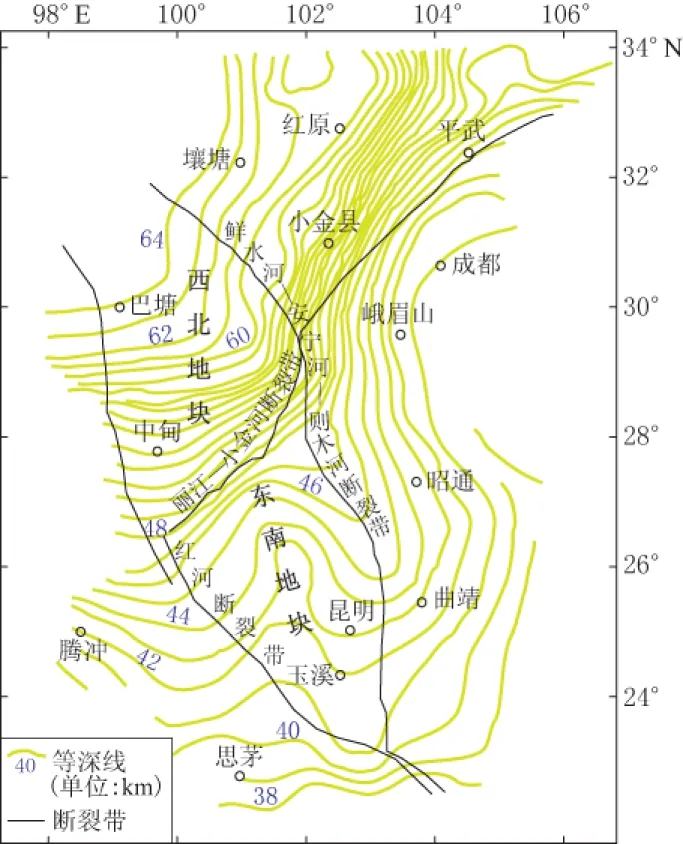
图2 川滇地区莫霍面等深线分布图

3.3 川滇菱形地块的应变速率

由于1970年通海MS7.8地震和1973年炉霍MS7.6地震前并无与本地块相关的形变数据， 故取近年来川滇菱形地块及其邻近地块的主张应变、 主压应变和剪应变的年平均应变速率进行研究． 对西北地块， 根据李延兴等（2009）应变场的测试结果， 巴颜喀拉地块区域（30.0°N—35.0°N、 98.0°E—101.5°E）1999—2007年平均主压应变、 主张应变及最大剪应变速率分别为2.08×10-8/a， 2.55×10-8/a和6.5×10-8/a． 依据李延兴和郭良迁（2002）测得的昆明及其邻区主压应变、 面应变和最大剪应变等值线图， 得到丽江—渡口地区（26.0°N—28.0°N、 99.0°E—102.0°E）1999—2001年平均面应变速率为0.7×10-7/a、 平均主压应变速率为0.8×10-7/a和平均剪应变速率为1.4×10-7/a． 从青藏高原相对于华南地块运动的速度场来看（李延兴等， 2009）， 川滇菱形地块西北地块剪应变速率取二者均值为10.25×10-8/a， 其与（28.0°N、 100.5°E）地区剪应变速率相等； 而主压应变速率均值为5.04×10-8/a； 按其剪应变、 主压应变的增加比例， 主张应变速率取值为5.44×10-8/a．

依据李延兴和郭良迁（2002）测得的昆明及其邻区主压应变、 面应变和最大剪应变等值线图， 将昆明南部1999—2001年平均主压应变速率1.1×10-7/a、 主张应变速率1.0×10-7/a（取值与面应变速率相同）和剪应变速率1.5×10-7/a分别作为川滇菱形地块东南地块的主压、 主张和剪应变速率．

3.4 川滇菱形地块的应变能积累

现有测量只给出两个方向的主应变（最小和最大主应变）， 中间主应变ε22靠推算得出．

若ε22=（ε11+ε33）/2， 则2（w23+w12）=w13； 若ε22趋近于ε11或ε33， 则2（w23+w12）=2w13． 由于实测结果ε22一般总偏离（ε11+ε33）/2， 但也不会等于ε11或ε33， 故取其平均得

2（w23+w12）=1.5w13.

（12）

由式（4）、 （7）和（12）可得

（13）

根据式（13）和式（9）可粗略地得到川滇菱形地块的总应变能． 其东南地块的应变能积累为

1010×10-14（Δt）2=1.977（Δt）2×1013；

（14）

西北地块的应变能积累为

1010×10-16（Δt）2=1.612（Δt）2×1013.

（15）

3.5 川滇菱形地块自1700年以来应变能积累的变化

自1700年以来， 川滇菱形地块周边50km范围内共发生M≥6.7地震33次， 其震中分布如图1所示． 其中在东南地块有14次， 包括M<7.0地震5次，M7.0—7.4地震5次，M7.5—7.9地震3次，M8.0地震1次； 西北地块有16次， 包括M<7.0地震6次，M7.0—7.4地震6次，M7.5—7.9地震4次； 两地块交界处有3次， 分别为云南剑川M6、 丽江M7.0和四川盐源M6.7地震．

3.5.1 川滇菱形地块东南地块应变能积累和释放（强震）随时间的变化特征

东南地块M≥7.5地震有4次， 分别为1733年云南东川紫牛坡M7、 1833年云南嵩明M8、 1850年四川西昌—普格M7和1970年云南通海MS7.8地震． 从资料分析看， 该地块的应变能积累释放周期比较完整的有两个， 大约均为120年（图3）． 1733年紫牛坡强震之前为一个不完整周期． 按上述原则， 第一周期从1733年起始． 第二周期从相邻两次强震的后一次强震， 即从四川西昌—普格M7地震的发震时间1850年开始． 这样， 第一周期从1733年起始， 至1850年结束， 紧接着第二周期开始． 1970年云南通海MS7.8地震发生， 第二周期结束， 第三周期开始． 由式（14）得到东南地块全部应变能积累随时间增长的平滑曲线（图3a）， 以及由式（11）得到包含每次强地震能量释放及其后应变能重新积累的锯齿状增长曲线（图3a）可以看出： ① 从一个新周期开始， 大约有20年左右或更长时间不会发生M≥6.7强震， 30年左右不会发生M≥7.0强震； ② 120年积累的应变能为1017.454J， 预测的强震震级约为M7.89， 然而这些应变能并非仅由一次、 而是由几次强震所释放， 其中M≥7.0的地震就有4次； ③ 每个周期中M≥7.0强震发生之后至下一次强震发生时， 地块所积累的应变能均不足以形成后一次强震， 然而从周期开始到每次强震发生， 地块积累的应变能包括扣除已发生强震所消耗的能量， 均足以形成本次强震； ④ 第二周期应变能积累释放曲线显示， 每次强震所积累的应变能在扣除已发生强震所消耗的能量后所预测的强震震级均高于实际发生的强震震级， 只有1970年的强震预测震级与实际震级相同（表1）， 而对于第一周期， 前两次的预测震级均高于实际震级， 只有1833年嵩明M8强震预测震级为M7.7； ⑤ 这些强震的发生在时间上没有规律， 只是随着时间积累， 应变能迅速增加， 可能发生的最大地震震级会增大．

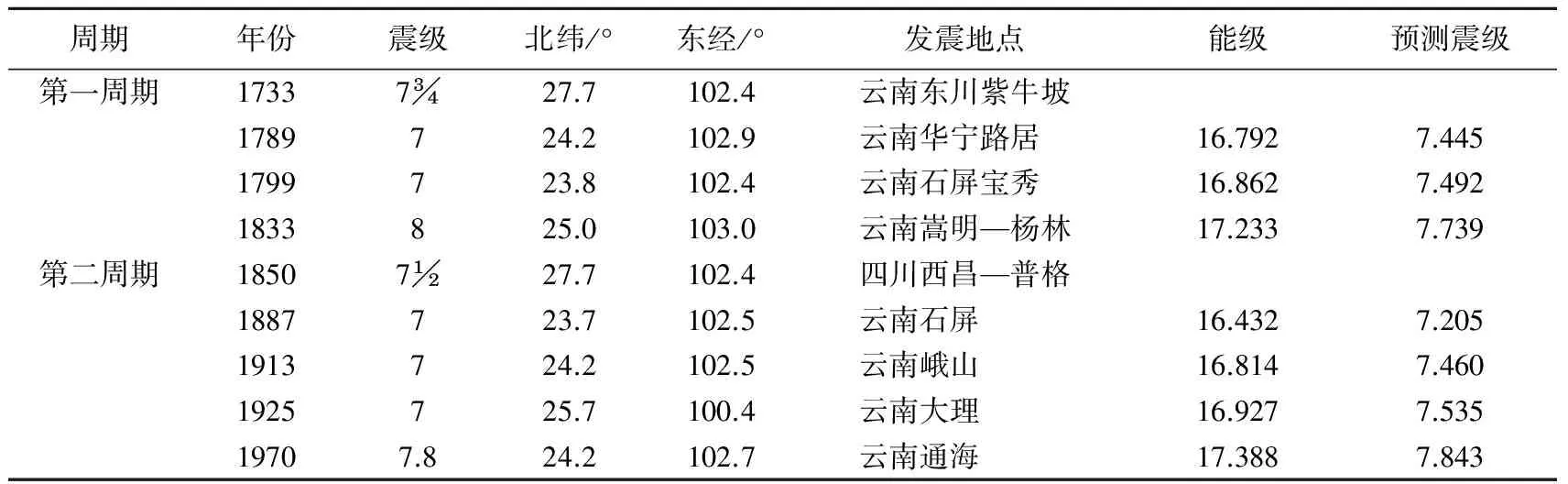
表1 川滇菱形地块东南地块强震震级（M≥7.0）与用应变能积累释放曲线所预测震级的比较Table 1 Comparison of the magnitudes of strong earthquakes （M≥7.0） with those predicted by strain energy accumulating-releasing curve in southeastern Sichuan-Yunnan rhombic block

3.5.2 川滇菱形地块西北地块应变能积累和释放（强震）随时间的变化特征

西北地块M≥7.5的地震有4次， 分别为1786年四川康定南M7、 1816年四川炉霍M7、 1955年四川康定折多塘一带M7.5和1973年四川炉霍MS7.6地震． 与上述原则相同， 该地块比较完整的应变能积累释放周期起始时间取为1816年， 结束时间为1973年， 时间间隔大约为160年． 1973年开始进入下一个周期（图3b）． 与图3a相同， 平滑曲线为西北地块全部应变能积累曲线， 而锯齿状曲线为包含每次强震能量释放及其后应变能重新积累的曲线． 可以看出： ① 从一个新积累周期开始， 大约有20年或更长时间内不会发生M≥6.7强震， 35年左右不会发生M≥7.0强震； ② 周期157年所积累的应变能为1017.60J， 预测强震震级约为M7.98， 同样这些应变能并非仅由一次、 而是由几次强震所释放， 其中M≥7.0的地震就有8次； ③ 该周期内M≥7.0强震之后到下一次强震发生时地块所积累的应变能， 不足以形成后一次M≥7.0强震， 然而从本周期开始到每次强震发生， 其间地块积累的应变能， 包括扣除已发生强震所消耗的能量， 均可以形成本次强震； ④ 对该周期内每次预测的强震震级均高于或略高于实际震级（表2）； ⑤ 这些强震的发生在时间上没有任何规律， 但随着时间增长， 可能发生的最大地震的震级会增大．

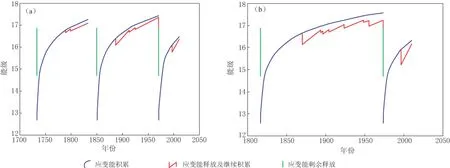
图3 川滇菱形地块东南地块（a）和西北地块（b）应变能积累释放周期及强震活动曲线，图中纵坐标为对实际积累的应变能取对数的结果

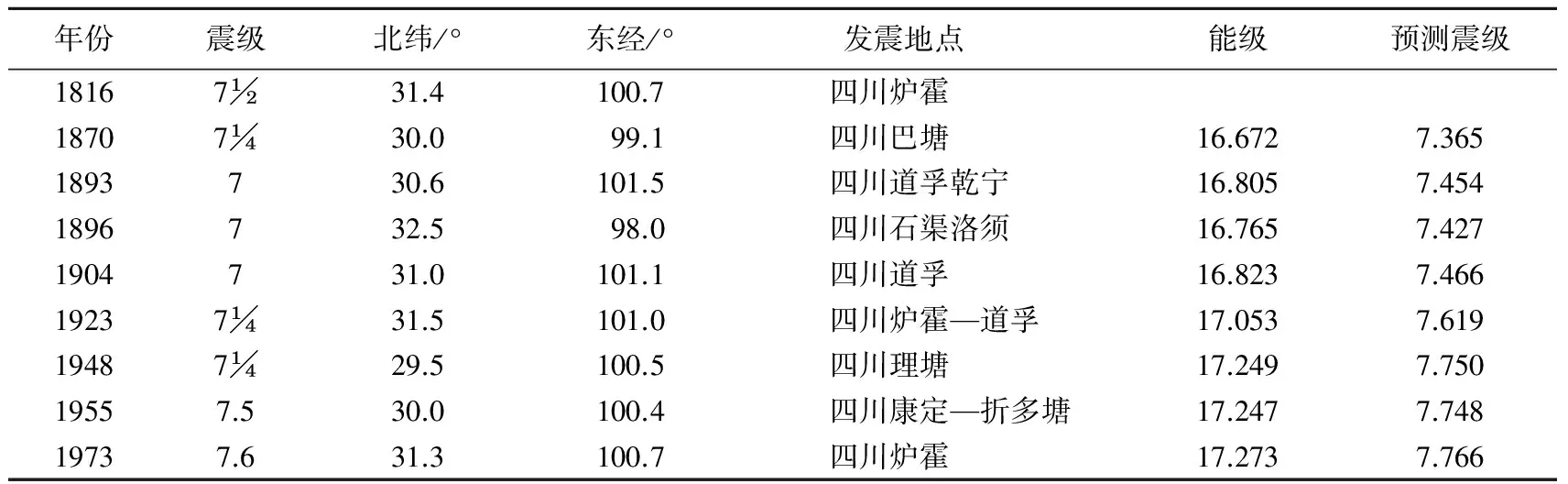
注： 1816年四川炉霍M7地震至1973年四川炉霍MS7.6地震为应变能积累释放的一个周期.

3.5.3 两地块应变能积累和释放（强震）随时间变化的共同特点

从图3可以看出， 两地块的应变能积累和释放随时间的变化具有以下共同特点：

1） 周期性． 东南地块一个周期大约为120年， 西北地块大约为160年． 由地块一个周期所积累的最大应变能推算出强震的最大震级： 东南地块为M7.89， 西北地块为M7.98．

2） 地震的平静期． 在一个周期的初期， 东南地块地震平静期约为30年， 西北地块约为35年， 在此期间不会发生M≥7.0强震． 而要形成M≥7.5强震， 东南地块约需70年， 西北地块约需80年．

3） 地震的活跃期． 每个地块一个周期所积累的应变能不是由一次强震一次释放完， 而是由几次M≥7.0强震逐步释放．

4） 根据应变能积累释放周期及强震活动曲线只能预测强震最大震级， 而无法预测强震发生时间． 而且， 强震只在地块边缘或内部发生， 一般不会在同一地点重复发生．

5） 目前两个地块均已具备发生M7.0地震的条件， 但近年内不会有M≥7.5强震发生． 对发震时间和地点的预测需根据其它前兆特征来确定．

4 地块边界强震最大震级的测算

1996年2月3日丽江MS7.0地震发生在两个地块的交界处． 到1996年， 西北地块已积累应变能1015.930J（图3b）， 东南地块已积累应变能1016.126J（图3a）， 仅一个地块积累的应变能很难达到发生M7.0地震的能量， 但两者相加其应变能积累可达1016.340J， 足以形成M7.0地震． 此外， 从1816—1973年西北地块所发生的强震震级与预测震级相近， 即使预测震级偏小， 其原因也是未将相邻地块积累的应变能予以累加所致． 至于1833年云南嵩明M8地震， 其预测震级仅为M7.7， 两者相差更多． 引起这种差别的原因很多， 其中一个原因是未将相邻地块积累的应变能进行累加所致； 另外主要影响因素可能是当年的应变速率比现在大． 因此在预测地块交界处的强震震级时， 一定要将相邻地块积累的应变能进行累加． 此外， 相邻地块发生强震后将引起本地块的应力调整， 可能会使本地块积累的应变能减少或改变积累速率， 推迟或加速本地块强震的发生． 综上， 在预测某一地块强震活动时除本地块应变能积累释放特征外， 还必须注意相邻地块的影响．

5 讨论与结论

1） 讨论了将地块应变能的积累释放周期与强震活动联合研究的意义． 如前文所述， 图3完全不同于传统的地震应变释放曲线， 它既包含了强震应变能释放， 也包含了地块总应变能的增加． 此外， 图3还显示了应变能积累从小到大直到最后完全释放的周期性特征． 时至今日， 在论及地震活动周期时， 均指的是对某一区域的强震在时间域上所重复出现的间隔． 而本文研究结果表明， 对一个固定活动地块， 地震活动周期类似于完整岩石破坏试验和黏滑试验中应变能随时间的变化． 强破裂对应于强震， 最终破坏对应于最后的特大强震（许昭永等， 2009）． 在加载前期， 应力、 应变随时间增加， 应变能也随时间增加． 但由于这一时期， 地块内总应变能还较低， 虽然在地块边缘或内部断层端部也有一些应力集中， 但由于积存能量较少， 因此没有强震（M≥7.0）发生， 这一时期为平静期． 随着时间的增加， 应变能持续增加． 在地块的多个应力集中部位， 先后达到强震条件（如应变能密度因子达到或超过临界值）， 并且已积累了发生强震足够的能量． 但此地震是在应变能的上升积累期发生的， 一次强震只是释放了一小部分能量. 随着时间推移， 应变能继续增加， 于是形成了锯齿状起伏增长的曲线． 直到周期末尾， 以一、 二次特大强震形式将绝大部分应变能释放而结束． 发生强震的这一时期为活跃期， 合起来为一个平静活跃周期． 由于活跃期的第一次强震发生时， 其应力强度还未达到破坏强度的一半， 而是由于在特殊部位的应力集中而导致地震的发生， 这就使得在应力速率均匀时， 地震活跃期比平静期要长， 甚至长很多． 这也解释了图3显示的地震活跃期比平静期长很多的原因． 显然， 应变能积累从小到大直到最后完全释放的周期性导致了地震的平静活跃周期． 然而， 地震活跃期的这些强震从时间上并无任何规律． 因此以应变能的积累释放周期来研究强震活动特征， 其物理意义将更明确， 该周期即为地块能量积累到能够发生极大强震（M8.0左右）所需的时间． 由于各个地块的应力和应变速率不尽相同， 材料性质如弹性模量、 断裂韧性等也不尽相同， 因此对于不同地块其最大能量积累释放周期也可能不同（图3）； 而对于同一地块， 其在不同时期的应力和应变速率不尽相同， 能量积累释放周期也会不同（图3）． 综上， 本文以地块最大能量积累释放周期讨论地震平静活跃循环周期完全不同于前人的研究． 尽管川滇地块能量积累释放周期明显， 但对其它地块还需作深入研究．

由图1和图3还可以看出， 应以适当的活动地块为单位进行应变能积累释放和强震活动综合研究． 若将图3a， b两个地块合并为一个川滇地块进行分析， 其周期性反而看不清． 因为在太大的地理范围内包含多个地块， 而各个地块在不同时期所积累的应变能大小不同， 发震条件或孕震时间长短也不同． 若将大范围多个地块的信息混合在一起， 会相互制约甚至造成混乱， 无法显示有效物理量的规律性． 因此对大地域范围讨论地震平静活跃周期是不合适的． 同时， 图1和图3也明确显示， 地震活跃期的强震并不一定在同一地点上发生， 只是在同一地块上能够引起强震的地方发生． 这就是我们主张的以活动地块为单位进行地震平静活跃周期研究的依据． 若仅以原地重复发生地震进行研究， 则川滇菱形地块的很多强震都难以找出规律． 同样， 也不会得出在汶川会发生MS8.0地震的结论．

综上所述： 对于单个地块， 可以讨论地震平静活跃循环周期， 但不宜讨论单次强震的复发周期； 大区域地理范围因其含有多个地块， 也不宜讨论其地震平静活跃周期．

2） 讨论了以地块应变能积累释放预测强震活动特征的可行性． 本文并非对特定地点， 而是对整个活动地块上可能发生强震的最大震级进行预测． 与其它定量地学问题一样， 在估算地块应变能积累总量时， 本文也作了诸多简化假设， 这可能使结果具有很大的不确定性．

首先， 对利用式（1）精确计算地块应变能可能产生的的误差进行了讨论． 从式（2）、 （3）可知， 应变能密度测量误差主要由弹性常数和应变测量所引起． 依据李延兴等（2009）对应变测量误差的分析， 该误差一般为3%—10%， 多数约为5%． 而弹性常数测量误差则主要由密度和波速所引起． 根据王椿槦等（2003）对波速测量的分析， 该误差一般为2%—5%． 二者相加， 应变能密度测量误差最小很难小于10%， 最大也不超过30%． 依据式（10）， 前者对震级的影响仅为0.003， 后者为0.08． 即对于精确测量（有限元法计算）， 该误差对震级大小预测几乎没有影响．

其次， 对用多个小地块平均应变或平均应变能密度计算地块应变能所产生的误差进行了讨论． 李延兴等（2009）对巴颜喀拉地块分为几个测区， 本文分别以平均应变或平均应变能密度计算了各地块应变能． 结果显示， 平均应变能密度法误差最大可达85%， 平均应变法最大为98%． 依据式（10）， 即使对能量高估一倍， 或低估50%， 震级偏差也只有0.2级． 更极端些， 能量偏差10倍（即10W或W/10）， 震级也只偏差0.7级． 另外， 从本文震例来看， 以地块应变能预测的强震震级与实际震级相当吻合（表1， 2）， 预测结果与实际偏差均小于0.5级． 因此， 本文结果虽然有一定的不确定性， 但完全满足地震安全性评价对潜在地震最大震级预测的精度要求， 而其相应的计算却简化了很多． 当然， 在资料足够和条件许可时， 也可尽量将地块划分更小， 采用式（1）和式（9）计算地块应变能， 可以减小误差． 因此， 本文方法预测震级是可行的， 至少不会比实际震级低太多， 可避免使抗震设防烈度偏离实际太多．

本文方法只是一种探讨， 计算条件仍有待改进． 例如， 地块应变能密度不可能处处均匀， 应力、 应变速率也不会永远为常数， 所用应变速率并非本地块实测， 深部应力、 应变状态未必与地表一致， 以及各测区主应变和应变速率及剪切应变能差异较大等． 诸如此类的问题有待进一步研究解决． 由于将应力、 变形、 大地构造和历史地震等诸多因素综合为应变能一个物理量， 因此以活动地块应变能积累释放周期和历史强震综合研究地震活动特征， 其物理意义是明确的． 本文结果对于地震安全性评价工作可能有重要意义．

蔡静观， 刘正荣. 1990. 以近期地震活动计算未来强震[J]. 中国地震， 6（3）: 47--52.

Cai J G， Liu Z R. 1990. Forthcoming strong earthquakes calculated upon recently seismic activities[J].EarthquakeResearchinChina， 6（3）: 47--52 （in Chinese）.

陈祖安， 林邦慧， 白武明， 程旭， 王运生. 2009. 2008年汶川8.0级地震孕震机理研究[J]. 地球物理学报， 52（2）: 408--417.

Chen Z A， Lin B H， Bai W M， Cheng X， Wang Y S. 2009. The mechanism of generation of May 12 2008MS8.0 Wenchuan earthquake[J].ChineseJournalofGeophysics， 52（2）: 408--417 （in Chinese）.

黄永祥， 黄润秋， 许强， 郭竟宇， 李延兴， 黄浩雄. 2002. 昆明玉溪研究区GPS和Kaiser应力测量结果与数值拟合反演[J]. 地震研究， 25（增刊A）: 48--56.

Huang Y X， Huang R Q， Xu Q， Guo J Y， Li Y X， Huang H X. 2002. The mathematical model fitting and related inversion of the values of crustal stress measured through GPS method and Kaiser method in Kunming and Yuxi research areas[J].JournalofSeismologicalResearch， 25（Suppl A）: 48--56 （in Chinese）.

皇甫岗， 陈颙， 秦嘉政， 李忠华， 安晓文， 杨周胜. 2010. 云南地震活动性[M]. 昆明: 云南科技出版社: 23--30， 108.

Huangfu G， Chen Y， Qin J Z， Li Z H， An X W， Yang Z S. 2010.TheSeismicityinYunnan[M]. Kunming: Yunnan Science and Technology Press: 23--30， 108 （in Chinese）.

李延兴， 郭良迁. 2002. 昆明及其邻区的地震活动趋势估计[J]. 地震研究， 25（增刊A）: 12--16.

Li Y X， Guo L Q. 2002. An estimation of seismic activity tendency in Kunming and its neighbouring regions[J].JournalofSeismologicalResearch， 25（Suppl A）: 12--16 （in Chinese）.

李延兴， 张静华， 周伟， 胡新康， 郭良迁， 张中伏. 2009. 汶川MS8.0地震孕育发生的机制与动力学问题[J]. 地球物理学报， 52（2）: 519--530.

Li Y X， Zhang J H， Zhou W， Hu X K， Guo L Q， Zhang Z F. 2009. The mechanism and dynamics of the generation and occurrence for WenchuanMS8.0 earthquake[J].ChineseJournalofGeophysics， 52（2）: 519--530 （in Chinese）.

刘启元， 李昱， 陈九辉， 郭飚， 李顺成， 王峻， 张绪奇， 齐少华. 2009. 汶川MS8.0地震: 地壳上地幔S波速度结构的初步研究[J]. 地球物理学报， 52（2）: 309--319.

Liu Q Y， Li Y， Chen J H， Guo B， Li S C， Wang J， Zhang X Q， Qi S H. 2009. WenchuanMS8.0 earthquake: Preliminary study of the S-wave velocity structure of the crust and upper mantle[J].ChineseJournalofGeophysics， 52（2）: 309--319 （in Chinese）.

王椿槦， 吴建平， 楼海， 周民都， 白志明. 2003. 川西藏东地区的地壳P波速度结构[J]. 中国科学: D辑， 33（增刊）: 181--189.

Wang C Y， Wu J P， Lou H， Zhou M D， Bai Z M. 2003. P-wave crustal velocity structure in western Sichuan and eastern Tibetan region[J].ScienceinChina:SeriesD， 46（Suppl）: 254--265.

许绍燮. 1982. 地震活动性图象述评[C]∥大陆地震活动和地震预报国际学术讨论会论文集. 北京: 地震出版社: 3--29.

Xu S X. 1982. A review of the seismicity patterns[C]∥ACollectionofPapersofInternationalSymposiumonContinentalSeismicityandEarthquakePrediction（ISCSEP）. Beijing: Seismological Press: 3--29 （in Chinese）.

许昭永， 王彬， 胡毅力， 杨润海. 2009. 试论岩石破裂和破坏的差异对地震模拟及前兆研究的影响[J]. 地球物理学报， 52（3）: 712--719.

Xu Z Y， Wang B， Hu Y L， Yang R H. 2009. A discussion on the influence of the difference between rock fracture and

failure to earthquake simulation and precursor studies[J].ChineseJournalofGeophysics， 52（3）: 712--719 （in Chinese）.

许昭永， 胡毅力， 许峻， 张建国. 2010. 应变能积累在地震安全性评价中的应用探讨[J]. 地震学报， 32（1）: 77--87.

Xu Z Y， Hu Y L， Xu J， Zhang J G. 2010. A discussion on application of strain energy accumulation to seismic safety evaluation[J].ActaSeismologicaSinica， 32（1）: 77--87 （in Chinese）.

尹祥础. 2011. 固体力学[M]. 北京: 地震出版社: 58--65， 388--427.

Yin X C. 2011.SolidMechanics[M]. Beijing: Seismological Press: 58--65， 388--427 （in Chinese）.

张国民， 耿鲁明， 石耀霖. 1993. 中国大陆强震轮回活动的计算机模型研究[J]. 中国地震， 9（1）: 20--32.

Zhang G M， Geng L M， Shi Y L.1993. A computer model for cyclic activities of strong earthquake in continental seismic zones[J].EarthquakeResearchinChina， 9（1）: 20--32 （in Chinese）.

张培震， 邓起东， 张国民， 马瑾， 甘卫军， 闵伟， 毛凤英， 王琪. 2003. 中国大陆的强震活动与活动地块[J]. 中国科学： D辑， 33（增刊）: 12--19.

Zhang P Z， Deng Q D， Zhang G M， Ma J， Gan W J， Min W， Mao F Y， Wang Q. 2003. Active tectonic blocks and strong earthquakes in the continent of China[J].ScienceinChina：SeriesD， 46（Suppl）: 13--24.

张培震， 徐锡伟， 闻学泽， 冉永康. 2008. 2008年汶川8.0级地震发震断裂的滑动速率、 复发周期和构造成因[J]. 地球物理学报， 51（4）: 1066--1073.

Zhang P Z， Xu X W， Wen X Z， Ran Y K. 2008. Slip rates and recurrence intervals of the Longmenshan active fault zone， and tectonic implications for the mechanism of the May 12 Wenchuan earthquake， 2008， Sichuan， China[J].ChineseJournalofGeophysics， 51（4）: 1066--1073 （in Chinese）.

周永胜， 何昌荣. 2009. 汶川地震区的流变结构与发震高角度逆断层滑动的力学条件[J]. 地球物理学报， 52（2）: 474--484.

Zhou Y S， He C R. 2009. The rheological structures of crust and mechanics of high angle reverse fault slip for WenchuanMS8.0 earthquake[J].ChineseJournalofGeophysics， 52（2）: 474--484 （in Chinese）.

Gutenberg B， Richter C F. 1942. Earthquake magnitude， intensity， energy， and acceleration[J].BullSeismolSocAm， 32（3）: 163--191.

Kanamori H. 2001. Energy budget of earthquakes and seismic efficiency[C]∥EarthquakeThermodynamicsandPhaseTransformationsintheEarth’sInterior，InternationalGeophysicsSeries，Volume76. San Diego， California: Academic Press： 293--305.

Scholz C H. 1996.TheMechanicsofEarthquakesandFaulting[M]. 2nd ed. New York: Cambridge University Press: 1--504.

Shimazaki K. 1976. Intra-plate seismicity and inter-plate earthquake: Historical activity in southwest Japan[J].Tectonophysics， 33（1/2）: 33--42.

Thatcher W. 1983. Nonlinear strain buildup and the earthquake cycle on the San Andreas fault[J].JGeophysRes， 88（B7）: 5893--5902.

Wang B， Xu Z Y， Yin X C， Hu Y L， Yang R H， Cai J G， Chen S Y. 2006. Experimental study of the earthquake recurrence period and the trend of post-seismic development[J].PureApplGeophys， 163: 2545--2560.

The strain energy accumulating-releasing period and strong earthquake prediction in Sichuan-Yunnan rhombic block

1）KunmingSouthernGeophysicalTechnologyCo.，Ltd，Kunming650091，China2）SchoolofResourceEnvironmentandEarthSciences,YunnanUniversity，Kunming650091，China3）ChinaEarthquakeNetworksCenter，Beijing100045，China4）EarthquakeAdministrationofYunnanProvince，Kunming650224，China

In this paper, the Sichuan-Yunnan rhombic block is divided into two parts. The strain rate is achieved by deformation, the elastic modulus is acquired by velocity structure in the deep, the volume of the block is calculated by the area and thickness of block, and then the variation of accumulated strain energy with time is confirmed. On this basis, combined with the research of historical strong earthquakes, the relationship between the period of energy accumulating-releasing and the seismic activity is obtained. The results show that the strain energy accumulating-releasing emerges periodically, which can be used for strong earthquake prediction. The strong earthquakes （M≥7.0） do not occur at initial stage of strain energy accumulation. The strain energy increases continuously with time and then several strong events occur firstly, but each event is smaller in magnitude than the predicted ones,i.e., one event releases a small part energy and later energy increases incessantly. The energy is not completely released until one or two great strong events （M≥7.5） occur. Thus, the old cycle ends and a new cycle starts. Obviously, the quiet to active periods are caused by the cycle of strain energy accumulation from small to great, and then to completely releasing. Active stage is much longer than the quiet one. Therefore, it is unsuitable to discuss the quiet-active period for a great geographic area covered by many blocks or to discuss the repeat period of single strong earthquake for a small region. Although the occurrence of strong earthquakes does not obey any law in time, the magnitude predicted by the strain energy accumulating-releasing curves is coincident with the real one, which may be significant for seismic safety evaluation.

active block; strain energy; accumulating-releasing period; activity of strong earthquakes; earthquake prediction

国家重点基础研究发展（973）计划项目（2013CB733200）和云南省教育厅科学研究基金项目（2012C110）共同资助.

2014-09-04收到初稿， 2015-03-12决定采用修改稿.

e-mail: zhaoyongx@126.com

10.11939/jass.2015.05.006

P315.72+7

A

许昭永, 文丽敏, 石宝文, 许峻, 樊俊屹, 李正媛, 苏有锦. 2015. 川滇菱形地块的应变能积累释放周期和强震预测. 地震学报, 37（5）: 774--786. doi:10.11939/jass.2015.05.006.

Xu Z Y, Wen L M, Shi B W, Xu J, Fan J Y, Li Z Y, Su Y J. 2015. The strain energy accumulating-releasing period and strong earthquake prediction in Sichuan-Yunnan rhombic block.ActaSeismologicaSinica, 37（5）: 774--786. doi:10.11939/jass.2015.05.006.