机床温度测点优化方法研究及试验验证

丛 明，李泳耀，孙宗余，李宏坤

（1.大连新宇理工科技开发中心有限公司，辽宁 大连 116024；2.大连理工大学 机械工程学院，辽宁 大连 116024；3.一汽解放汽车有限公司无锡柴油机厂，江苏 无锡 214026）

0 引 言

机床的热误差是由其零部件间因温升变化而导致不同程度的热变形引起的，这种误差最终会累积到刀具和工件上，引起其相对位置的偏移，影响机床的加工精度［1］.研究表明，热误差占机床总误差的比例往往在40%～80%，越是精密的机床，所占比例越大［2－3］.目前，热误差建模与补偿技术是一种有效减小热误差，提高机床加工精度的手段［4］，而实现热误差建模与补偿的前提是进行机床温度测点的优化，它直接决定了热误差模型的精确性和鲁棒性.

近年来，国内外学者对温度测点优化问题进行了大量的研究，提出了许多相关理论和方法，如灰色关联度法［5］、有限元法［6］、逐步多元回归法［7］等.每种理论都各有优缺点，如灰色关联度法虽然很好地解决了温度测点相对于整机温度场具有的小样本、贫信息的问题，但仅以测点与热误差间的紧密程度来优化测点，指标单一，容易误判；有限元法是基于机床温度场和热变形场的，该方法虽然简单，但机床各零部件间结合面的边界条件及热荷载很难准确获得，因此实际结果并不理想；逐步多元回归法只考虑了温度变量与热误差间的相关性，忽视了温度变量间的耦合现象，虽然能获得较高的预测精度，但模型鲁棒性较低.结合每种理论的优点，也有学者提出了多种理论相结合的方法，如模糊聚类与相关分析法［8］、灰色关联与模糊聚类法［9］等，这些方法同时考虑了各温度测点间及测点与热误差间的相关性，收到了很好的优化效果.

本文采用多种理论相结合的方法来实现机床温度测点的优化.采用简单相关分析，剔除掉与热误差明显不相关的温度测点.对筛选出的测点进行模糊聚类，消除各测点间相关性的影响.同时对筛选出的测点进行灰色综合关联度分析，判断各测点对热误差的影响程度.分别建立多个不同测点的热误差模型，并对模型参数进行统计分析，最终得到用于建立热误差模型的关键温度测点.

1 温度测点优化相关理论

1.1 简单相关分析

简单相关分析是用来研究变量间关联程度的一种统计方法，采用相关系数来表征.这里采用Pearson相关系数来研究各温度测点与热误差间的相关程度，公式如下：

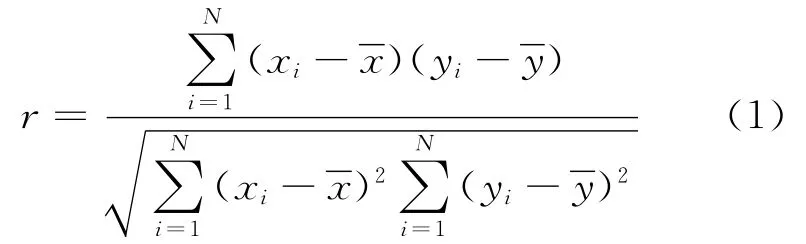
具体判断规则如表1所示.同时，采用t统计量对Pearson相关系数检验，t统计量服从n－2个自由度的t分布.

表1 简单分析的基本原理Tab.1 Basic principle of simple analysis

1.2 模糊聚类分析

模糊聚类分析主要是通过建立模糊关系，来对各变量进行聚类［9］.分析步骤如下：

（1）标准化样本数据

对温度变量数据进行标准化处理，以简化矩阵运算过程，亦可避免出现奇异阵，中断分析过程.这里采用极差变换法，公式如下：

（2）建立模糊相似矩阵

模糊相似矩阵R＝（rij）p×p的构造有多种方法，这里采用相关系数法.设p个温度变量的集合X＝（x1x2…xp），其中xi＝（xi1xi2…xim）（i＝1，2，…，p）为第i个变量的m个观测值，则定义rij为描述变量x、y间关联程度的相关系数，其计算公式为

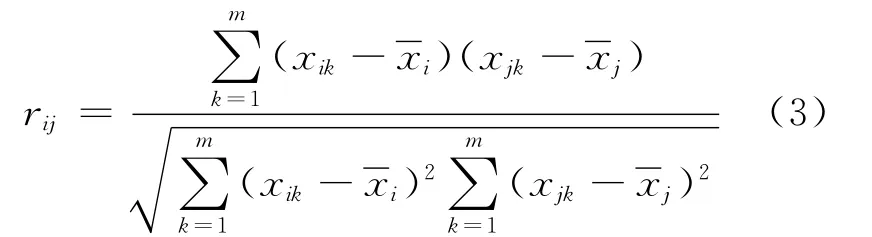
（3）建立模糊等价矩阵

建立的模糊相似矩阵虽然满足自反性、对称性，但不一定满足传递性，实现合理聚类的前提是模糊矩阵要同时满足这3个条件.这里采用平方法将模糊相似矩阵R变换出一个模糊等价矩阵（传递闭包t（R）），经过有限次运算后，存在k使得R2k＝R2（k＋1），令t（R）＝R2k，t（R）即为所求的模糊等价矩阵.

（4）聚类分析

从t（R）中提取阈值λ（λ∈［0，1］），不同的λ对应不同的温度变量分类结果，最终形成动态聚类图.

1.3 灰色综合关联度分析

所采集的温度测点数据相对于整机温度场来讲，具有小样本、贫信息等特点［10］，采用灰色系统分析能较好地解决这一问题，主要分为灰色绝对关联度分析、灰色相对关联度分析及灰色综合关联度分析.

（1）灰色绝对关联度

设Xi＝（xi（1）xi（2） …xi（n））为系统行为序列，令

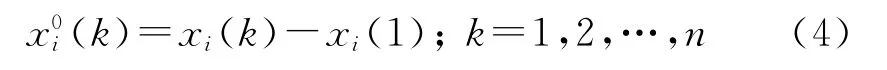
则XiD＝X0i＝（x0i（1）x0i（2） …x0i（n））为Xi的始点零化像，D称为始点零化算子.

记热误差序列为X0，温度测点i的序列为Xi，其始点零化像分别为

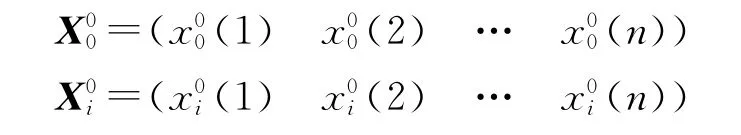
则定义

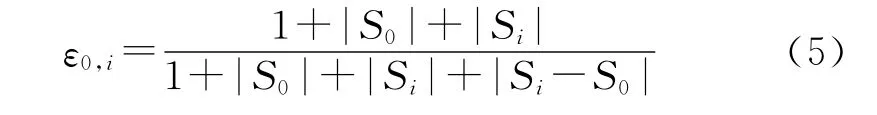
为Xi相对X0的灰色绝对关联度.其中

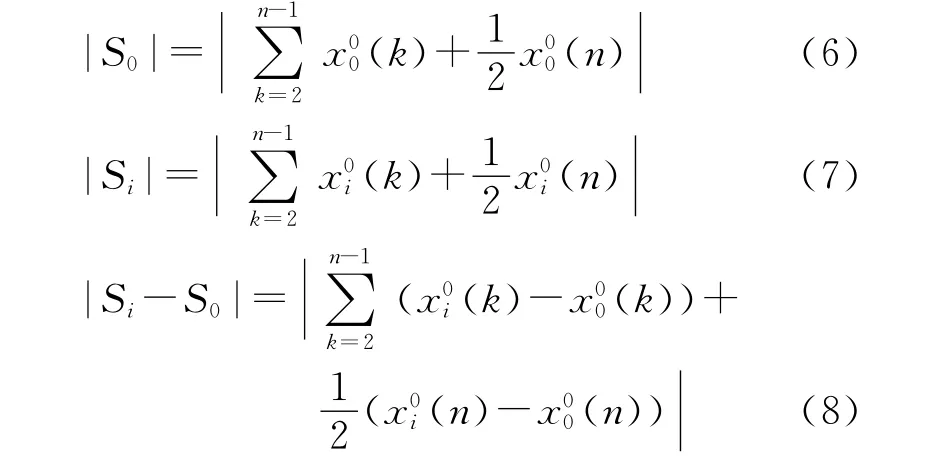
（2）灰色相对关联度

设Xi＝（xi（1）xi（2） …xi（n））为系统行为序列，令

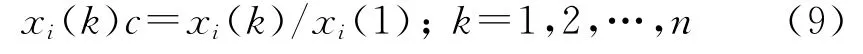
则XiC＝X′i＝（xi（1）cxi（2）c…xi（n）c）为Xi的初值像，C为初值化算子.

记热误差序列为X0，温度测点i的序列为Xi，其初值像分别为

根据式（4），计算得到X′0和X′i的始点零化像

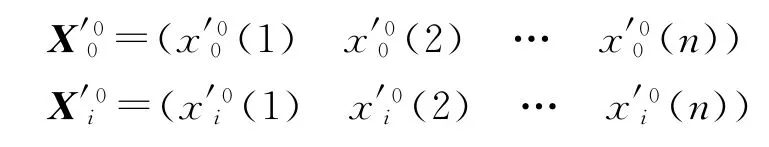
分别称为X0和Xi的初值始点零化像.定义

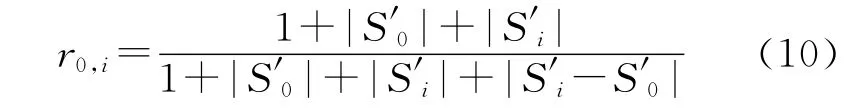
为Xi相对X0的灰色相对关联度.其中

（3）灰色综合关联度

记ε0，i和r0，i分别为两序列X0和Xi的灰色绝对关联度和灰色相对关联度，定义

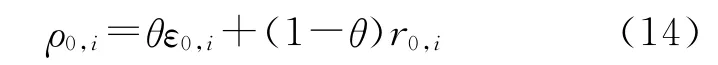
为X0和Xi的灰色综合关联度.其中θ∈［0，1］，用来调整绝对关联度与相对关联度相对于综合关联度的影响程度，一般取θ＝0.5.

2 试验分析和结果验证

2.1 试验方案

以某型号卧式加工中心为研究对象，在各热源位置处布置20个温度传感器（图1），具体安装位置如表2所示.采用电涡流位移传感器测量机床主轴Z向热误差，如图2所示.试验采用空切削方式，为尽量模拟实际加工情况，工况设置如表3所示.

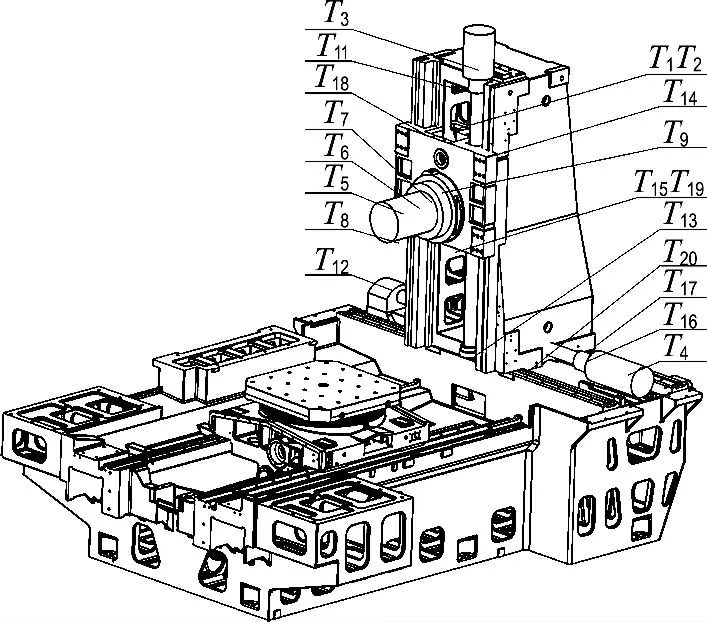
图1 温度传感器布置图Fig.1 Arrangement plan of temperature sensors

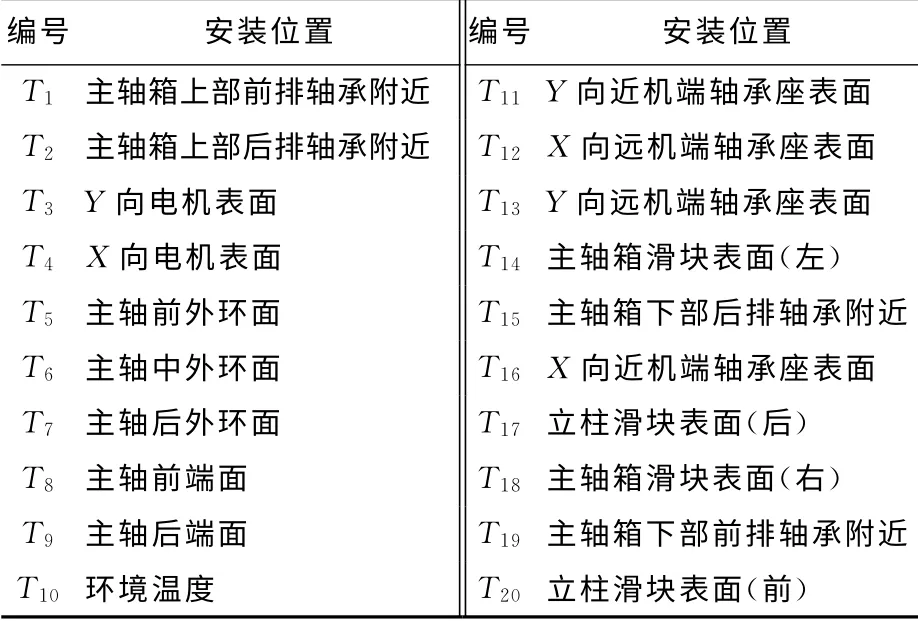
表2 温度传感器安装位置Tab.2 Installation position of temperature sensors

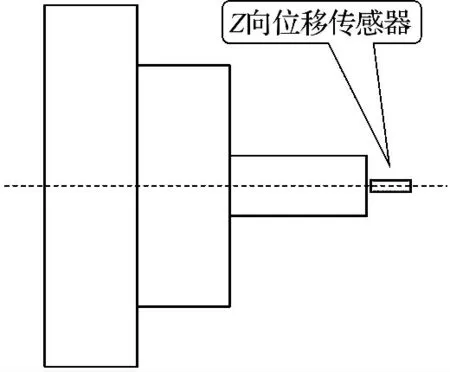
图2 Z 向位移传感器布置图Fig.2 Arrangement plan of displacement sensors at Z－direction

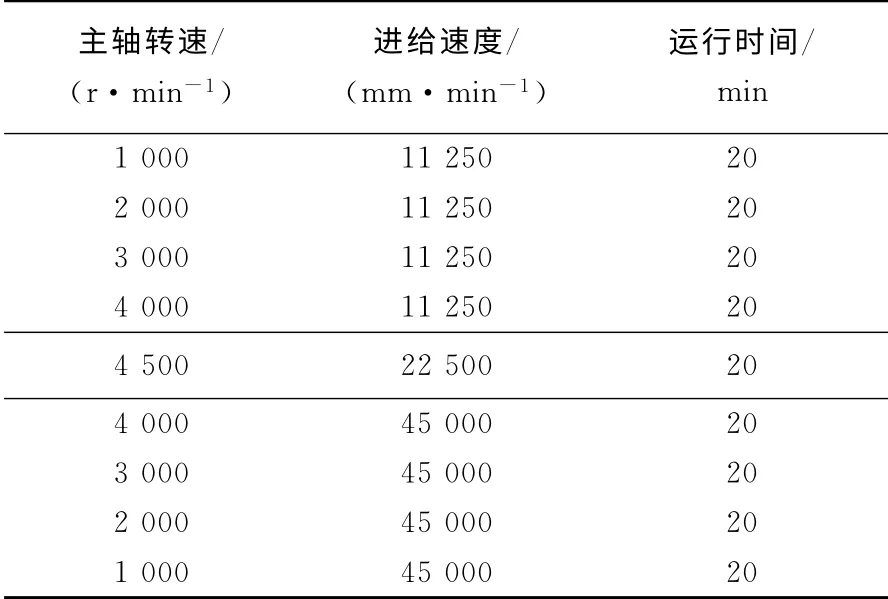
表3 试验工况设置Tab.3 Setting of test conditions

2.2 测点优化结果

根据简单相关分析理论，首先计算出主轴Z向热误差与各温度测点间的相关系数，并采用t统计量对Pearson相关系数进行检验，结果如表4所示.然后依据表1规则，筛选掉非显著性相关及未通过假设检验的温度测点，初步得到优化后的15个温度测点（ΔTi，i＝1，2，…，15，表示相对于初始温度值的变化量，下同）：ΔT1、ΔT2、ΔT3、ΔT4、ΔT5、ΔT6、ΔT7、ΔT8、ΔT9、ΔT10、ΔT11、ΔT12、ΔT13、ΔT14、ΔT15.

根据模糊聚类方法，对筛选出的15个温度变量进行聚类分析，聚类结果如图3所示.

表4 简单相关分析结果Tab.4 Results of simple correlation analysis

同时，采用灰色综合关联度分析法，以主轴Z向热误差为母序列x0，15个温度测点变量为子序列xi（i＝1，2，…，15），计算各子序列与母序列间的灰色关联度，计算结果如下：

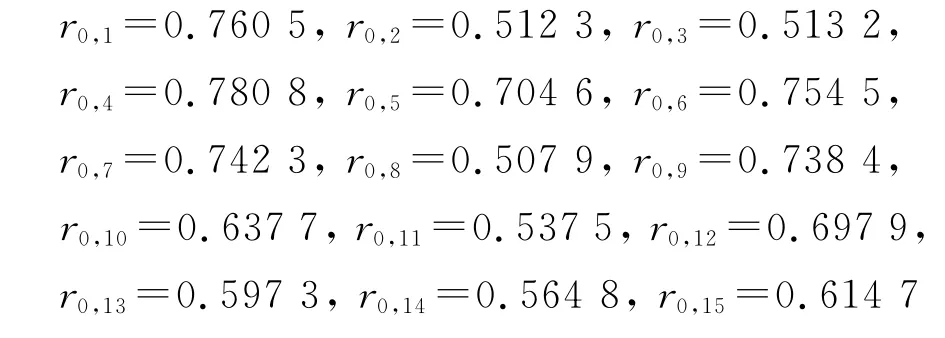
图3 动态聚类图Fig.3 Dynamic clustering map

根据模糊聚类分析及灰色关联度计算结果，将15个温度变量分为2类、3类、4类、5类、6类，相对应地分别建立2测点、3测点、4测点、5测点及6测点（若多个测点属于同一类，则取灰色关联度值大的测点用于建模，例如：若分两类，则ΔT3、ΔT8、ΔT10、ΔT14属于同一类别，取灰色关联度值最大的ΔT10作为建模用测点）的基于多元线性回归的热误差模型.对模型进行基于统计学理论的分析，结果如表5所示.

对表5进行分析，可以得出如下结果：

（1）对回归模型的方差分析采用F检验，每个模型的概率P（即显著性Sig.）均小于显著性水平0.05，故所建立的模型是具有统计学意义的，即热误差与各测点之间的线性关系是显著的［11］.

（2）R∈［0，1］为复相关系数，表征自变量和因变量间线性回归关系的密切程度，其值越大回归关系越密切.调整R2反映模型的拟合效果，其值越大说明拟合效果越好.剩余标准差（残差的标准差）表征了模型预测结果的精确度，其值越小预测效果越好.从表中可以看出，采用越多测点建立的模型的R及调整R2越大，剩余标准差越小，但其变化率是逐渐减小的，也就是说测点越多，虽然建立的模型精度越高，但精度的提高却越来越不明显.

（3）采用越多测点建立的模型的最大残差越小，但采用6测点建立的模型的最大残差却有增大趋势，说明此时模型精度已经很难得到明显的提高.即使采用6个以上的测点建立的模型精度高，但由于测点过多，用来建模亦是不可取的.

（4）5测点模型中的ΔT1没有通过t检验，且通过偏相关系数可以看出，ΔT1对模型的贡献率很小.

通过以上分析，以5测点的模型为依据，剔除掉ΔT1，最终选择ΔT4、ΔT6、ΔT10、ΔT12为关键温度测点（图4），重新建立模型，并对回归模型进行分析，结果如表6所示.模型均通过了t和F检验，且最大残差达到了最小.

2.3 结果验证

根据温度测点优化结果，采用多元线性回归法建立的热误差模型为

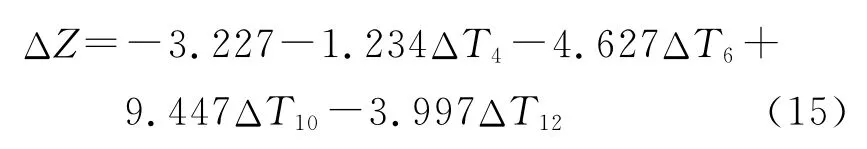
式中：ΔZ为机床主轴Z向热误差.

表5 多元线性回归模型分析Tab.5 Analysis of multiple linear regression model

图4 关键温度测点数据Fig.4 Data of key temperature measuring points

该模型（记为模型1）的热误差预测曲线如图5所示.

若依旧采用本文思路，但未进行回归模型分析，根据模糊聚类和灰色综合关联度结果，直接选取4个关键温度测点（ΔT1、ΔT4、ΔT6、ΔT10）建立热误差模型（记为模型2），预测曲线如图6所示.

若直接采用灰色综合关联度法，选取4个关键温度测点（ΔT1、ΔT4、ΔT6、ΔT7）建立热误差模型（记为模型3），预测曲线如图7所示.

表6 优化后的回归模型分析Tab.6 Analysis of regression model optimized

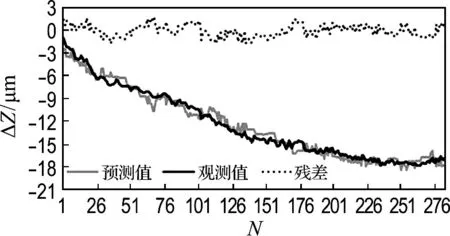
图5 模型1的热误差预测图Fig.5 Thermal error prediction map in model 1

图6 模型2的热误差预测图Fig.6 Thermal error prediction map in model 2

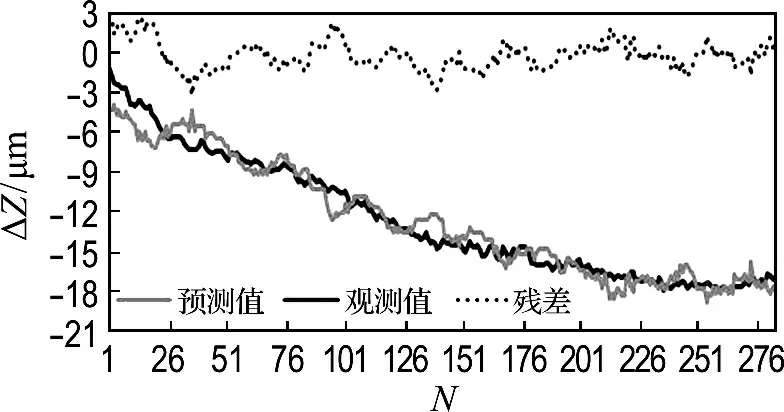
图7 模型3的热误差预测图Fig.7 Thermal error prediction map in model 3

对比3种方法的热误差模型预测精度，结果如表7所示.

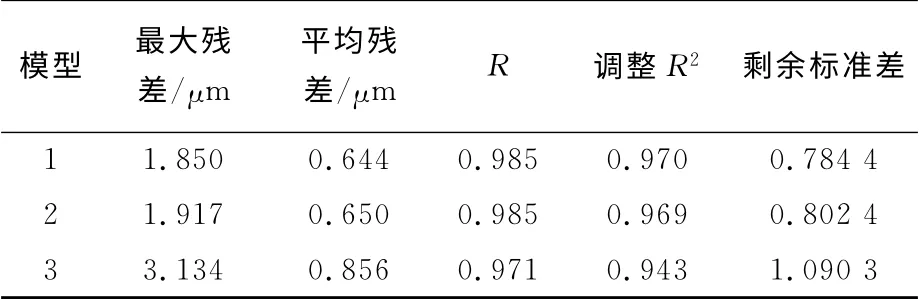
表7 热误差模型预测结果Tab.7 Prediction results of thermal error models

从表7可以看出，采用本文方法建立的热误差模型，最大残差仅有1.850μm，平均残差亦只有0.644μm，且调整R2和剩余标准差也达到了较理想的效果，说明采用本文方法优化出的温度测点能较为全面地反映出温升变化对主轴Z向热误差的影响程度，模型预测精度较好.

3 结 论

（1）采用本文方法对卧式加工中心进行了温度测点优化及模型预测精度的试验验证，使用于建模的测点由20个降至4个，主轴Z向热误差从17.903μm 减小到1.850μm.

（2）对比3种不同的温度测点优化方法，并对建立的热误差模型进行分析，得出：采用本文方法优化得到的温度测点所建立的热误差预测模型，其平均残差只有0.644μm，最大残差亦仅为1.850μm，预测效果优于另外两种方法.

（3）利用统计学理论，在对回归模型全面分析的基础上筛选出关键测点，有效避免了多温度变量在热误差模型中的复共线性问题，大大提高了模型的精确性和鲁棒性.

［1］ Ramesh R，Mannan M A，Poo A N.Error compensation in machine tools—a review partⅡ：thermal errors［J］.International Journal of Machine Tools and Manufacture，2000，40（9）：1257－1284.

［2］ 凡志磊，李中华，杨建国.基于偏相关分析的数控机床温度布点优化及其热误差建模［J］.中国机械工程，2010，21（17）：2025－2028.FAN Zhi－lei，LI Zhong－hua，YANG Jian－guo.NC machine tool temperature measuring point optimization and thermal error modeling based on partial correlation analysis［J］.China Mechanical Engineering，2010，21 （17）：2025－2028.（in Chinese）

［3］ Pahk H J，Lee S W.Thermal error measurement and real time compensation system for the CNC machine tools incorporating the spindle thermal error and the feed axis thermal error ［J］.International Journal of Advanced Manufacturing Technology，2002，20（7）：487－494.

［4］ YANG Jian－guo，YUAN Jing－xia，NI Jun.Thermal error mode analysis and robust modeling for error compensation on a CNC turning center ［J］.International Journal of Machine Tools and Manufacture，1999，39（9）：1367－1381.

［5］ 李永祥，童恒超，杨建国.灰色系统理论在机床热误差测点优化中的应用［J］.机械设计与研究，2006，22（3）：78－81.LI Yong－xiang，TONG Heng－chao，YANG Jianguo.Application of grey system theory in optimizing the measuring points of thermal error on machine tools［J］.Machine Design and Research，2006，22（3）：78－81.（in Chinese）

［6］ Kim S K，Cho D W.Real－time estimation of temperature distribution in a ball－screw system［J］.International Journal of Machine Tools and Manufacture，1997，37（4）：451－464.

［7］ Lo Chih－hao，YUAN Jing－xia，NI Jun.Optimal temperature variable selection by grouping approach for thermal error modeling and compensation［J］.International Journal of Machine Tools and Manufacture，1999，39（9）：1386－1396.

［8］ 马术文，徐中行，刘立新，等.XH718加工中心的热误差补偿研究［J］.机械科学与技术，2007，26（4）：511－514.MA Shu－wen，XU Zhong－xing，LIU Li－xin，etal.A study on thermal error compensation for the spindle of XH718machining center［J］.Mechanical Science and Technology，2007，26（4）：511－514.（in Chinese）

［9］ 张 伟，叶文华.基于灰色关联和模糊聚类的机床温度测点优化［J］.中国机械工程，2014，25（4）：456－460.ZHANG Wei，YE Wen－hua.Optimization of temperature measuring points for machine tools based on grey correlation and fuzzy clustering analysis［J］.China Mechanical Engineering，2014，25（4）：456－460.（in Chinese）

［10］ 闫嘉钰，张宏韬，刘国良，等.基于灰色综合关联度的数控机床热误差测点优化新方法及应用［J］.四川大学学报（工程科学版），2008，40（2）：160－164.YAN Jia－yu，ZHANG Hong－tao，LIU Guo－liang，etal.Application of a new optimizing method for the measuring points of CNC machine thermal error based on grey synthetic degree of association［J］.Journal of Sichuan University（Engineering Science Edition），2008，40（2）：160－164.（in Chinese）

［11］ 杨建国，范开国.数控机床主轴热变形伪滞后研究及主轴热漂移在机实时补偿［J］.机械工程学报，2013，49（23）：129－135.YANG Jian－guo，FAN Kai－guo.Research on the thermal deformation pseudo－lag and real－time compensation for CNC machine tool spindle［J］.Journal of Mechanical Engineering，2013，49（23）：129－135.（in Chinese）