基于蚁群迭代算法的近似测地线计算
2015-03-20龚燕,杨洁,吴微
龚 燕,杨 洁,吴 微
(大连理工大学 数学科学学院,辽宁 大连 116024)
0 引 言
测地线的计算分为精确计算和近似计算.由于难于求出测地曲率,精确计算方法在实际操作中基本无法运用.近似计算有很多方法,例如Kanai等[1]和童晶等[2]先后对三角网格上的近似测地线算法做了研究.但Kanai等的方法计算精度很低,并且容易陷入局部最优.童晶等针对其容易陷入局部最优的问题进行了改进,提出了三角网格上的迭代细分算法,同时还提高了迭代运算速度和精度,然而该算法的收敛性和给定误差下的计算复杂度还未做理论的分析,实际运用起来仍然有着一定局限性.杨斌等[3]和杜培林等[4]分别研究了点云模型上的近似测地线计算,但他们的算法均采用固定的网格模型,需要建立目标函数以及求解解析式,精确度不高同时操作难度很大.
基于以上问题,本文提出一种蚁群迭代算法计算近似测地线.
1 算法详述
1.1 操作假设
假设对于区域ΩR3中任意一点可通过某种方法确定其三维坐标,那么在该区域中,任意两点之间的近似距离可通过坐标计算求得.例如,任意A、B∈R3,A点坐标为(x1,y1,z1),B点坐标为(x2,y2,z2),则A、B之间的近似距离可通过下式得到:在这样的条件下,任给某种地形,本文希望用蚁群迭代算法求出给定的两点之间的近似测地线.
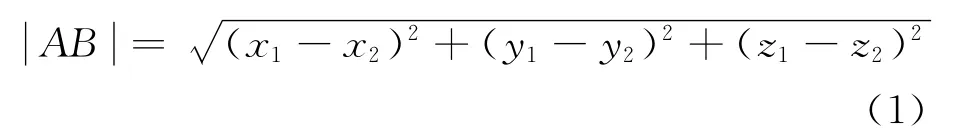
首先将待求两点之间的地形在相应的垂直映射平面图上作任意网格划分,再不断加密划分,每一步划分得到相应的网格模型后都用蚁群算法计算最短路径,这样可以通过迭代计算自适应地寻找最佳网格规模,解决网格划分不适当造成的误差,并且在计算过程中不需要地形解析式或其他方程式.
1.2 蚁群迭代算法具体操作
(1)将A、B两点之间的地形(如图1所示)垂直映射到平面上(如图2所示),在图2上作适当的正方形网格划分,即将横纵坐标轴进行等分操作,用5×5表示分别进行五等分,10×10表示分别进行十等分,依此类推.用蚁群算法在初始网格划分上找出A、B两点的最短路径.
(2)对上一步的网格划分作成倍加密划分,例如上一步网格规模为5×5,则加密至规模10×10,并设置当前蚁群算法的初始信息素与上一步保留信息素比例为1∶1,再用蚁群算法在当前的划分上找出A、B两点的最短路径,且依然保留该路径上的信息素.
(3)重复步骤(2),反复迭代适当次数,直到寻找到最佳的测地线为止.

图1 原地形图Fig.1 Original topographic map

图2 图1的垂直映射平面图Fig.2 Vertical mapping planar graph of Fig.1
1.3 算法详解
在设计算法中,之所以保留上一步最短路径上的信息素是为了给下一步迭代以启示,让蚂蚁们有意识地偏向已有最短路径周围继续寻找更合适的路径,从而避免在整个范围内寻找最短路径的盲目性.但是这样做容易导致蚂蚁们几乎全部聚集在上一步最短路径周围,使得迭代效率大大降低.为解决此问题,本文设置每一步迭代时蚁群算法的初始信息素与保留信息素比例为1∶1,这样既能合理利用上一步迭代成果的资源,又不影响在整个范围内寻找最短路径.该比例的大小是否影响且将如何影响每一步迭代找出的最短路径,有待进一步讨论研究.
另外,在该算法中最关键的是获取网格点所对应的原地形上两点之间的曲面距离.由于整个地形可能很不规则,无法通过公式得到该距离,但也不可直接用两点之间的直线距离取而代之,因为初始网格划分密度通常不会太大,这样计算可能造成很大的不准确性.本文采取在网格点之间适当增加一些点,然后算出每一小段的直线距离,将其总和作为两个网格点之间的近似曲面距离的办法解决这一难题.例如,图3中的凹凸地形,假设平面上A″、B″两点是网格点,现需计算A″、B″两点所对应的原地形图上A′、B′之间的近似曲面距离,如果直接用连接A′、B′的直线距离代替,在初始网格划分不太细密的时候计算误差会较大,所以本文在A″、B″两点之间再等距插入一些点,例如插入C″点,其中C″点对应原地形图上的C′点,假 设A′的 坐 标 为(x1,y1,z1),B′的 坐 标 为(x2,y2,z2),C′的坐标为(x3,y3,z3),则A′、B′之间的曲面距离


图3 计算网格点之间距离示意图Fig.3 Schematic diagram of computing the distance between grid points
在1.1操作假设中已经提出,对于任意的地形,任给两点总是可以通过测量等方法得到其三维坐标,从而如式(2)所示计算出近似距离,那么蚁群迭代算法总是可运行的.
最后,为了保证加密前与加密后在计算网格点之间距离时的近似程度保持一致,在每一次迭代计算网格点之间的近似曲面距离时要对插入的点数作适当安排.例如,当划分的网格是5×5,计算两个网格点之间的近似曲面距离时在该两点之间不包括端点再插入31个点;加密之后,划分的网格是10×10,计算两个网格点之间的近似曲面距离时在该两点之间则应不包括端点再插入15个点;依此类推.
2 结果讨论
2.1 结果展示
经过验证,用蚁群迭代算法得到的一组最短路径数据呈现先降后升的结果.如图4的地形,欲从A点到B点求出一条近似测地线,网格规模分别为2×2、4×4、8×8、16×16、32×32、64×64,由每一个划分所得到的最短路径见表1.

图4 单峰原地形Fig.4 Original terrain of unimodal

表1 单峰地形的结果Tab.1 The results of unimodal terrain
结果显示,当网格规模为8×8或16×16时,最短路径大小下降到最低程度,再做加密划分,其大小呈现增长趋势.由此可知,蚁群迭代算法自适应地寻找到最佳网格规模为8×8或16×16,此时所得到的最短路径为最佳近似测地线路径.
再如图5的地形,欲从A点到B点求出一条近似测地线,网格规模分别为5×5、10×10、20×20、40×40、80×80,由每一个划分所得到的最短路径见表2.
再做网格规模分别为6×6、12×12、24×24、48×48、96×96,由每一个划分所得到的最短路径见表3.

图5 多峰原地形Fig.5 Original terrain of multimodal

表2 多峰地形的结果1Tab.2 The results of multimodal terrain(1)

表3 多峰地形的结果2Tab.3 The results of multimodal terrain(2)
由以上结果可知,表2的划分方式当网格规模为40×40时,得到最短路径;表3的划分方式当网格规模为48×48时,得到最短路径.综合比较可知,当网格规模为40×40时,所得到的最短路径为最佳近似测地线路径.
以上结果表明在加密到一定程度的时候继续加密已经没有效果,此时便已找到了最优化的路径.且结果路径图中还显示,即使加密过度之后最短路径的大小增大,但是很稳定地保持了最短路径的趋向,如图6和7所示.

图6 单峰地形的一组最短路径Fig.6 The set of shortest paths of unimodal terrain

图7 多峰地形的一组最短路径Fig.7 The set of shortest paths of multimodal terrain
2.2 结果分析
网格之所以加密到一定程度便失去加密效果,是因为此时加密过度,使得网格点之间的距离非常小,蚁群迭代算法使用轮盘赌的原则选择下一步走向,这时蚂蚁们很可能会在局部小范围内绕圈走弯路.另一方面,最短路径的大小是由该路径上相邻网格点之间的距离总和求得的,此时网格点之间距离很小,则总和便会增大,更何况此时已经保持了同一的最短路径趋向.所以由实验结果与理论分析可知,蚁群迭代算法确实能有效优化最短路径,而且该算法相对稳定,如本文中实例情形,一般在网格规模为40×40 时达到最佳效果.由于计算网格点之间的距离时近似程度要保持一致性,在加密过程中不可任意加密,应成倍加密.为了避免可能疏漏的某些网格规模,可通过更改初始划分密度,得到更多其他的网格规模,例如表3的最优结果为网格规模48×48,再使其与40×40的网格规模作比较,看是否得到更优化的最短路径,此处不再作详细示范.
3 结 语
本文提出了一种不依赖于地形解析式的近似测地线计算方法——蚁群迭代算法,该算法采用自适应的方式寻找最佳网格划分规模,克服了某些算法中固定网格划分未能达到最佳规模而造成的较大计算误差,从而能找出更加优化的最短路径,且在复杂、凹凸不平、障碍物多的地形上尤其适用.但本文对每一步迭代时蚁群算法的初始信息素与上一步迭代的保留信息素比例问题未做详细探讨,在不影响实验结果的情况下,暂时先设置为1∶1的比例,此问题有待进一步研究.
[1] Kanai T,Suzuki H.Approximate shortest path on apolyhedral surface and its applications[J].CAD Computer Aided Design,2001,33(11):801-811.
[2] 童 晶,陈正明.三角网格表面近似测地线的计算[J].计算机辅助设计与图形学学报,2008,20(2):180-185.TONG Jing,CHEN Zheng-ming.Approximate geodesics path on triangle mesh [J].Journal of Computer-Aided Design & Computer Graphics,2008,20(2):180-185.(in Chinese)
[3] 杨 斌,范媛媛,王继东.点云模型上近似测地线的计算[J].计算机应用,2011,31(4):1050-1052,1056.YANG Bin,FAN Yuan-yuan,WANG Ji-dong.Computation of approximate geodesics on point cloud[J].Journal of Computer Applications,2011,31(4):1050-1052,1056.(in Chinese)
[4] 杜培林,屠长河,王文平.点云模型上测地线的计算[J].计算机辅助设计与图形学学报,2006,18(3):438-442.DU Pei-lin,TU Chang-he,WANG Wen-ping.Computing geodesics on point clouds[J].Journal of Computer-Aided Design & Computer Graphics,2006,18(3):438-442.(in Chinese)
