基于移动协助方式的网络连通性恢复技术研究

迟百川，曹江涛，张 一，赵 婧，牛晓棠，邵鹏飞

（辽宁石油化工大学 信息与控制工程学院，辽宁 抚顺 113001）

0 引 言

近年来，无线传感器网络（wireless sensor network，WSN）的广泛应用引起了研究机构和工程界的高度关注［1］，其最引人注目的应用是能在无人值守的严酷环境（如战场监测、边境保护、太空探索等）中避免生命危险，减少工作成本，并且提供一个完全自动化的数据收集系统.在无线传感器网络的应用中，传感器节点处理能力有限，所以期望部署的传感器形成一个连通的网络，在执行任务时，相互协调工作，将收集的数据传送到基站（base station，BS）.由于传感器节点是电池供电的设备，它们面临能源耗尽、设备不工作的风险；另外，恶劣环境及恶意攻击也易使节点大规模损坏.在这些情况下，网络的通信链路断开，数据传输受到限制.

为恢复网络连通性，Cerpa等曾提出布置冗余节点的方案，其思想是采用斜坡算法，通过提高节点密度，来恢复无线传感器网络连通性并延长网络使用寿命［2］；Abbasi等提出重新布置一些节点的方案，其思想是运用DARA 算法来恢复无线传感器网络连通性［3］.这两种方案虽都能解决无线传感器网络连通性的问题，但却不适用于极端环境下节点的大规模损坏.在这种情况下，用剩余节点建立无线传感器网络各集群的连通性显得至关重要.

不同于固定中继节点的方式来建立静态通信链路［4］，本文运用移动数据收集器（mobile data collector，MDC）作为移动中继节点建立间歇性的通信链路，以恢复各集群间的连接.当移动数据收集器移动到传感器节点的传输范围内，将收集数据，然后沿着优化的路径移动并收集数据，最后将数据送往基站，以恢复网络的连通性.

1 问题描述

无人值守的无线传感器网络在严酷环境中，传感器节点易大规模损坏，网络被分割成多个不连通的子网络，节点数据无法传输给Sink节点，造成无线传感器网络不可用.而在无线传感器网络中引入移动元素可以有效地提升网络性能，包括降低能量消耗［5］、延长网络生存时间［6］等.所以本文采用移动数据收集器作为移动元素，其在能量存储和通信能力方面是一个很强大的设备［7］，通过它移动和携带各节点的数据以建立各集群间的通信链路，进而恢复网络连通性.

在无人值守的复杂环境下，移动数据收集器应通过收集各传感器节点数据，并以最小的路径移动来恢复网络的连通性，从而最小化缓冲要求和减少延迟.为解决上述问题，本文主要采取以下3个步骤：

（1）将剩余可用节点通过FCM 聚类算法大致分为K个集群，确保集群内部节点间相互通信，并确定集群中心点.

（2）选取收集点.在数据收集环节中，最重要的就是最佳收集点（collection point，CP）的选取.因此将移动数据收集器送到集群的位置侦查环境，并进行数据收集，当移动数据收集器移动到收集点处，就可获知该集群的信息.

（3）优化路径.寻找移动数据收集器移动的最短路径等同于旅行商问题，被认为是一个NPHard问题.本文采用Dijkstra算法［8］优化移动数据收集器的移动路径来解决该问题.

2 收集点的选取

当移动数据收集器移动到一个传感器的通信范围内时，它将收集数据.因此，收集点的选取变得非常重要.

模糊C均值（fuzzyC－Means，FCM）聚类算法［9］是一种迭代优化算法，其基本思想是将一组分布未知的数据进行分类，寻找隐藏在数据中的结构，按照某种相似程度的度量，尽可能地使具有相同性质的数据归于同一类［10］，适用于本文所研究的内容.因此，本文利用FCM 聚类算法首先将随机分布的节点划分为集群，并且确保集群内部相互通信，然后通过该算法确定集群中心点，为收集点的选取做准备.该算法可描述为

式中：U为输入空间X一个模糊C划分，V为聚类中心点集合，c为数据样本，n为形成聚类的个数，为加权指数［11］.

假设所有传感器具有相同的传输范围CR，做如下的定义：

定义1 通过FCM 聚类算法形成的K个集群S＝｛S1，S2，S3，…，SK－1，SK｝，各集群的中心点 集C＝ ｛C1，C2，C3，…，CK－1，CK｝，令Center1，2，…，K为中心点集C的中心点.

定义2 令rb为代表点（representative point，RP），满足rb与Center1，2，…，K之间的欧式距离最短，即mindist（rb，Center1，2，…，K）.

定义3PKb定义为集群S的收集点，满足dist（PKb，rb）≤CR.

然而，上述寻找收集点的方法只适合各集群所在位置的连线为凸形的情况.如图1所示，以4个集群S＝｛S1，S2，S3，S4｝为例，通过FCM 聚类得 到 的 中 心 点 集C＝ ｛C1，C2，C3，C4｝，Center1，2，3，4为聚类中心点集C的中心 点，在集群S中选出与Center1，2，3，4距离最短和次短的两个点作为代表点，然后分别与Center1，2，3，4连线，其与代表点传输范围CR的交点即被选择为收集点.

图1 各集群位置呈凸形时收集点的选取Fig.1 The selection of CP when clusters present convex

当各集群所在位置的连线为凹形时，需要找出具有凹点的集群，运用FCM 聚类算法确定该集群中心点C4，如图2所示，然后连接其他集群的收集点（此收集点的选取与凸形选取方式一致）.从C4向与之最近的边作垂线，垂足为Q，则垂线与代表点传输范围CR的交点P41即为该集群的收集点.

实际上，各集群的位置不仅仅呈现凸形或凹形，也可能呈现更为复杂的网状结构，但网状结构可分解为若干个凸形和凹形的情况.为此，本文只专注于集群位置呈凸形和凹形的情况.

图2 各集群位置呈凹形时收集点的选取Fig.2 The selection of CP when clusters present concave

3 最小化移动数据收集器移动路径

部署移动数据收集器的主要目的是传输数据，可通过设置移动数据收集器的移动路径来达到这个目的.假设移动数据收集器的移动路径T是一个最短循环，每个集群至少包含一个收集点.寻找T路径等同于旅行商问题，被认为是一个NP－Hard问题.由于移动数据收集器的移动路径可能包含一个集群中的两个收集点，需要挑选出每个集群的单收集点对路径进一步优化，来最小化移动路径.

为处理该问题，本文采用Dijkstra算法，该算法用于计算一个源节点到所有其他节点的最短代价路径.其基本思想是设置顶点集合S并不断地作贪心算法来扩充这个集合，直到扩展到终点为止，寻找最短路径的最优解，符合本文解决该问题的基本思路.

然而针对本文的具体问题，需构建选择最优路径模拟图，并且运用两次Dijkstra算法.其最短路径T可描述为

式（2）中上标表示收集点编号，下标代表集群编号，比如：CP｛1，2｝1表示P11、P12，即集群S1中的两个收集点.其最优路径选择分为以下3个步骤进行：

（1）求最短路径T1

（2）求最短路径T2

（3）T1与T2比较，选出最优路径Minroute

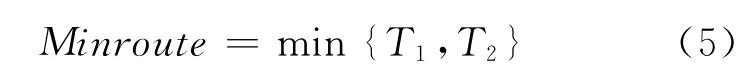
如图3所示，虚线框代表集群.首先以CP11（S1中P11点）为起始点，寻找到CP｛1，2｝4（S4中P41或P42点）的最短路径T1；然后再以CP21为起始点，寻找到CP｛1，2｝4的最短路径T2，比较T1、T2，选出最优路径Minroute.

图3 选择最优路径模拟图Fig.3 The simulation diagram of global optimal path selection

由上可知，由于集群所处位置的差异，收集点的选择方式也会不同，使得移动数据收集器的移动路径随之发生变化.本文从以下两种情况进行考虑：

（1）各集群所在位置连线为凸形

同样以4个集群为例.首先从集群S＝｛S1，S2，S3，S4｝中分别选取两个收集点：CP｛1，2｝1，CP｛1，2｝2，CP｛1，2｝3，CP｛1，2｝4，并对其进行路径规划，如图4所示.

挑选出单一收集点对移动数据收集器的移动路径进一步优化，选出最优路径Minroute，此时：

如图5所示，虚线即为移动数据收集器的最优移动路径，所经过的点即为挑选出的单一收集点.

图4 两个收集点形成的最短移动路径Fig.4 The shortest path formed by two CPs

图5 运用Dijkstra算法形成的单收集点移动路径Fig.5 Formation of single CP′s mobile path by using the Dijkstra algorithm

（2）各集群所在位置连线为凹形

这种情况比较复杂，需要考虑到具有凹点的集群.同样以4个集群为例，首先确定各集群的收集点，然后再对其进行路径优化，寻找最优路径Minroute.此时：

其形成过程如图6所示，虚线即为移动数据收集器的最优移动路径，所经过的点即为挑选出的单一收集点.

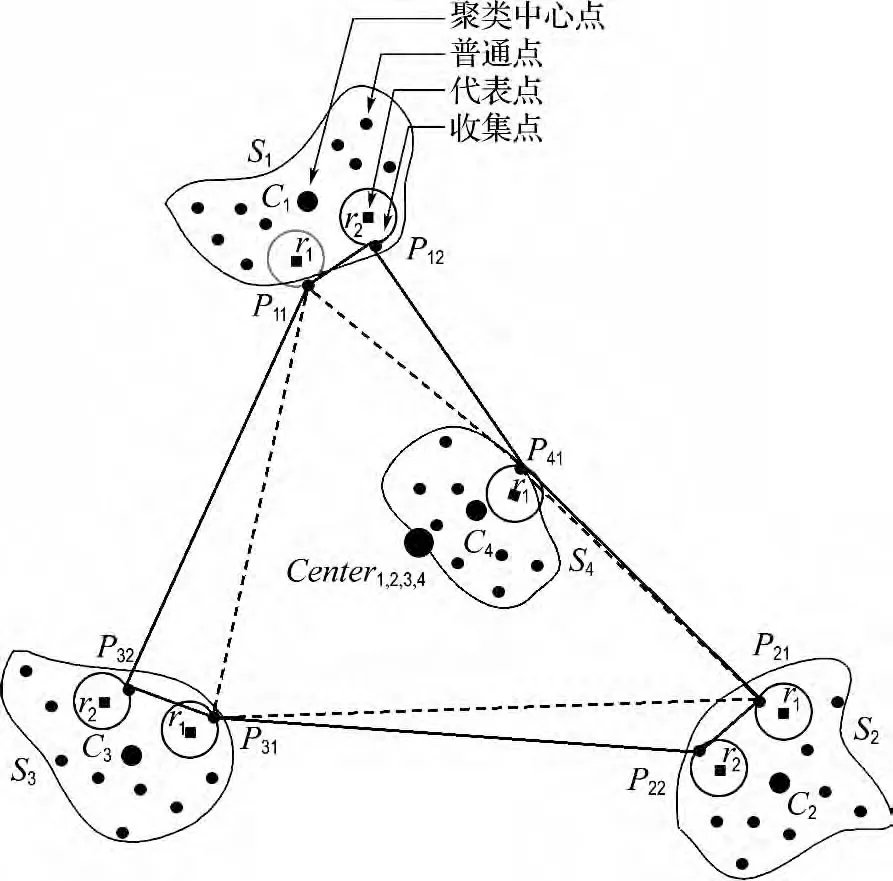
图6 各集群位置呈凹形时最优路径的形成过程Fig.6 The formation process of optimal path when clusters present concave

4 仿真测试及结果

本文运用Matlab2012a作为仿真平台进行结果测试.在1 m×1 m 的范围内随机布置100个节点，运用FCM 聚类算法将其聚类形成3～6个集群，并且保证其内部正常通信.定义传感器和移动数据收集器的传输范围为0.1 m.以下是仿真中性能指标：

（1）移动总长度（total tour length，TTL）：因为移动能减少移动数据收集器的使用寿命，所以最小化移动数据收集器的移动路径是该方案的一个设计目标.

（2）最大移动长度（maximum tour length，MTL）：反映移动数据收集器完成一个最短循环T所移动的最大长度L.如果L长度过大，将会导致数据收集的延迟增加，所以需要最小化L.

在已形成指定聚类数目的前提下，将本文方案与IDM－KMDC［12］进行比较.IDM－KMDC的主要思想是将节点形成指定数目集群后，在每个集群中选择一个收集点，然后运用最小生成树算法［13］进行路径规划，以达到移动数据收集器移动路径的最小化.

从表1中的数据可知，本文方案优于IDMKMDC，移动总长度较IDM－KMDC 平均减少了8.15%，即在移动数据收集器移动速度确定的情况下，能更好地恢复网络的连通性，并且当传感器节点形成6 个集群时，本文方案明显优于IDMKMDC.图7为其仿真图像.

表1 两种方案下移动总长度的比较Tab.1 The comparison of total tour length for two schemes

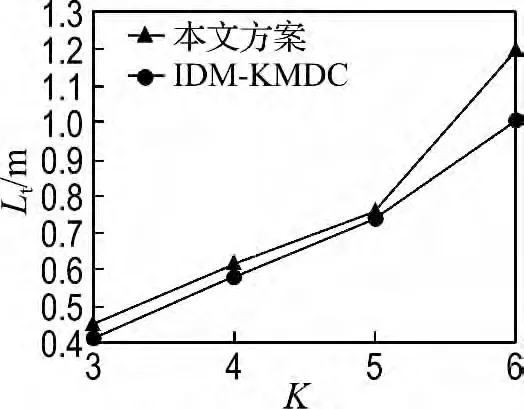
图7 两种方案下的移动总长度Fig.7 Total tour length for two schemes

表2为两种方案下最大移动长度的比较.由该表可知，本文方案的最大移动长度较IDMKMDC平均减少了17.20%，说明本文方案在数据收集的延迟上低于IDM－KMDC，网络运行的速度更快.其仿真图像如图8所示.

表2 两种方案下最大移动长度的比较Tab.2 The comparison of maximum tour length for two schemes

通过表1、2的实验结果可以看出，在已形成指定聚类数目的前提下，与IDM－KMDC 方案相比，本文方案能更快地恢复无线传感器网络的连通性，更适合极端环境中无人值守的无线传感器网络节点大规模损坏的情况.

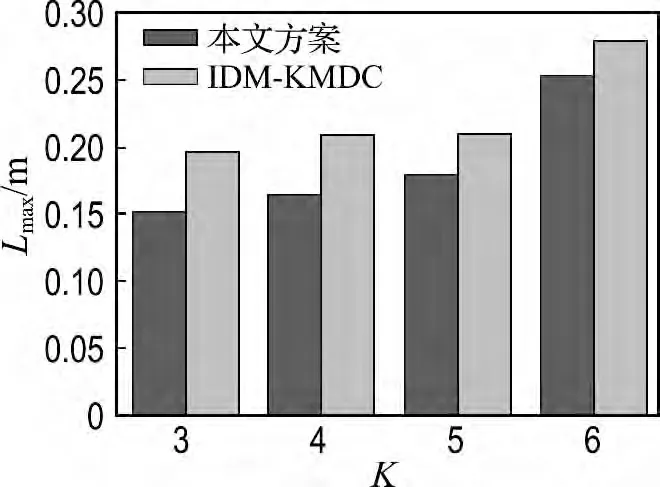
图8 两种方案下的最大移动长度Fig.8 Maximum tour length for two schemes

5 结 语

本文针对严酷环境中，无线传感器网络的大规模损坏，许多节点同时失效，造成网络通信中断的问题，提出了一种运用移动协助的方式来恢复网络连通性的方案.首先将剩余可用的节点进行聚类，然后寻找数据收集点，进行路径优化，以确保移动数据收集器移动路径的最小化，从而最小化缓冲要求，减少延迟.经过仿真测试，证明了该方案的可行性，并最小化了移动路径.建立实验系统模型，并将其运用到工业生产中，将是下一步研究的内容.

［1］ Estrin D，Girod L，Pottie G，etal.Instrumenting the world with wireless sensor networks ［J］.ICASSP，IEEE International Conference on Acoustics，Speech and Signal Processing －Proceedings，2001，4：2033－2036.

［2］ Cerpa A，Estrin D.ASCENT：Adaptive selfconfiguring sensor networks topologies［J］.IEEE Transactions on Mobile Computing，2004，3（3）：272－285.

［3］ Abbasi A A，Akkaya K，Younis M.A distributed connectivity restoration algorithm in wireless sensor and actor networks［C］／／Proceedings of the 32nd IEEE Conference on Local Computer Networks，LCN 2007.Los Alamitos：IEEE Computer Society，2007：496－503.

［4］ 傅菊平，王东方，齐小刚.放置中继节点解决无线传感器网络能量空洞问题［J］.微型机与应用，2011，30（2）：72－74.FU Ju－ping，WANG Dong－fang，QI Xiao－gang.Using relay－nodes to solve energy hole in wireless sensor networks ［J］.Microcomputer ＆ Its Application，2011，30（2）：72－74.（in Chinese）

［5］ Jain S，Shah R C，Brunette W，etal.Exploiting mobility for energy efficient data collection in wireless sensor networks［J］.Mobile Networks and Applications，2006，11（3）：327－339.

［6］ Luo J，Hubaux J P.Joint mobility and routing for lifetime elongation in wireless sensor networks［J］.Proceedings－IEEE INFOCOM，2005，3：1735－1746.

［7］ Kalyanasundaram B，Younis M.Using mobile data collectors to federate clusters of disjoint sensor network segments［C］／／2013IEEE International Conference on Communications，ICC 2013.Piscataway：IEEE，2013：1496－1500.

［8］ 蔚 洁，杨怀雷，成汝震.基于Dijkstra算法的最优路径搜索方法［J］.河北师范大学学报：自然科学版，2008，32（5）：590－593，598.YU Jie，YANG Huai－lei，CHENG Ru－zhen.Optimal path searching method based on Dijkstra algorithm［J］.Journal of Hebei Normal University：Natural Science Edition，2008，32（5）：590－593，598.（in Chinese）

［9］ 高新波.模糊聚类分析及其应用［M］.西安：西安电子科技大学出版社，2004.GAO Xin－bo.Fuzzy Cluster Analysis and Its Application［M］.Xi′an：Xidian University Press，2004.（in Chinese）

［10］ 朱 林，王士同，邓赵红.改进模糊划分的FCM 聚类算法的一般化研究［J］.计算机研究与发展，2009，46（5）：814－822.ZHU Lin，WANG Shi－tong，DENG Zhao－hong.Research on generalized fuzzyC－means clustering algorithm with improved fuzzy partitions ［J］.Journal of Computer Research ＆ Development，2009，46（5）：814－822.（in Chinese）

［11］ 姜 伦，丁华福.关于模糊C－均值（FCM）聚类算法的改进［J］.计算机与数字工程，2010，38（2）：4－6.JIANG Lun，DING Hua－fu.Improvement of the fuzzyC－means clustering algorithm ［J］.Computer＆ Digital Engineering，2010，38（2）：4－6.（in Chinese）

［12］ Senel F，Younis M.Optimized interconnection of disjoint wireless sensor network segments usingKmobile data collectors ［C］ ／／ 2012 IEEE International Conference on Communications，ICC 2012.Piscataway：IEEE，2012：492－496.

［13］ 王化宇.最小生成树算法及其应用［J］.内蒙古科技与经济，2011（6）：72－73.WANG Hua－yu.Minimum spanning tree algorithm and its application ［J］.Inner Mongolia Science Technology ＆ Economy，2011（6）：72－73.（in Chinese）