相位解包裹中欠采样问题的实验研究

郭 媛，陈小天，毛 琦

(齐齐哈尔大学计算机与控制工程学院，齐齐哈尔161006)

式中

引 言

数字散斑干涉测量技术是激光技术与数字图像处理相结合的光测方法。它具有精度高、灵敏度高、非接触无损测量等优点［1-3］。在数字散斑测量中，待测光场的相位分布是通过求反正切运算得到的，得到的包裹相位值被限制在(-π，π］之间，这就需要通过相位解包裹技术得到真实相位。近年来，随着光学测量技术的发展，很多相位解包裹方法被提出，如路径跟踪算法、最优估计算法、最小范数算法等［4-6］。其中最常用的算法是基于最小范数的最小二乘解包裹算法，最小二乘方法最后得到泊松方程，求解泊松方程的方法有迭代法［7］和直接法［8-9］。同时，最小二乘相位解包裹又分为非加权最小二乘相位解包裹和加权最小二乘相位解包裹［10-11］。

欠采样是由于干涉条纹较密集，而现有的CCD的有限空间带宽限制，使得计算机的取样间隔过大造成信息丢失造成的。CCD的空间宽带积越小，欠采样现象越严重。应用传统的相位解包裹算法将不能从欠采样包裹相位图中解出正确的连续相位分布，致使解包裹失败，这个问题一直是相位解包裹中的一个难点。

剪切干涉测量是光学测量中的一种重要的测量方法，它通过同一光波与它的一个小错位后的光波之间的干涉完成测量，根据剪切方向可分为横向剪切、径向剪切、旋转剪切和方向剪切等。有学者将横向剪切的理论引入欠采样相位解包裹中，能够有效地解决欠采样问题［12-15］。横向剪切干涉能够有效地去除欠采样现象的原因在于它利用波前相位与其自身小的错位之间的偏差往往很小的特点，然后通过对偏差进行处理，进而实现对欠采样包裹相位的恢复。但是，横向剪切只是在一定的范围内能够解决欠采样问题，当欠采样较严重、相位变化过快时，现有的横向剪切算法就会失效，不能正确地恢复正确的相位分布。本文中在横向剪切最小二乘相位解包裹算法(least square algorithm based on lateral shearing interferometry，LSBLS)的基础上提出新的相位解包裹算法，解决了欠采样带来的误差，提高了原有的相位解包裹算法的抗采样干扰能力，并通过理论分析和实验验证了其正确性和有效性。

1 横向剪切最小二乘算法原理

数字散斑干涉测量中，从相干图像提取的包裹相位为 ψi，j(- π≤ψi，j≤π)，与之对应的真实相位为 φi，j，并有:式中，ki，j为整数，(i，j)是 M × N 图片中像素点的坐标，0≤i≤M-1，0≤j≤N-1。

定义x方向和y方向上的包裹相位差分别为Δxi，j和 Δyi，j:

式中，W为包裹算子，其目的是对包裹相位偏导数进行加减 2π，从而确保 Δxi，j和 Δyi，j位于(- π，π］之间。

最小二乘相位解包裹算法的基本思想是寻求真实相位的偏导数和包裹相位差的差分的值最小，即:

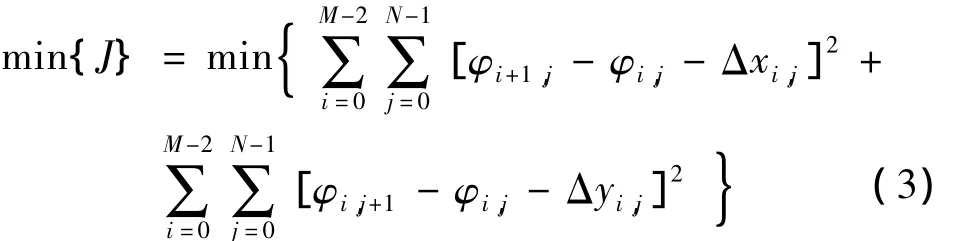
对(3)式φi，j求导数并令其为0，整理得泊松方程:

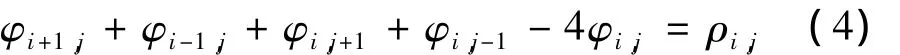
式中

因为相位微分在包裹相位图像边缘是无效的，故泊松方程的Neumann边界条件为:

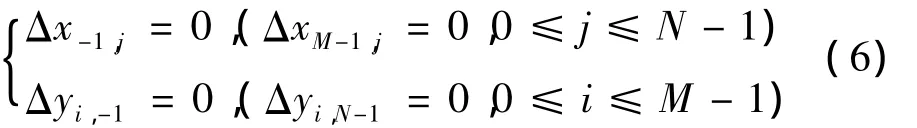
显然最小二乘相位解包裹算法转化为对泊松方程的求解，常用的求泊松方程的方法有迭代法和离散余弦变换(discrete cosine transform，DCT)或者快速傅里叶变换(fast Fourier transform，FFT)。

传统的方法是用上述方法求出包裹相位，当相位变化快而使解包裹失败。为解决这个问题，从而LSBLS算法被提出，其不同于传统的解包裹方法是引入剪切干涉的原理，在(2)式的基础上建立一个等效的2维复光场:

将两光场相除，即可得到新的光场:

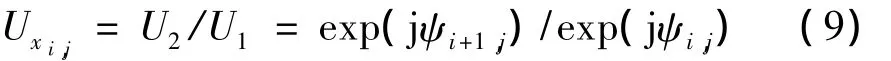
式中，Im()和Re()分别表示取复函数的虚部和实部运算。同理，在y方向上有:

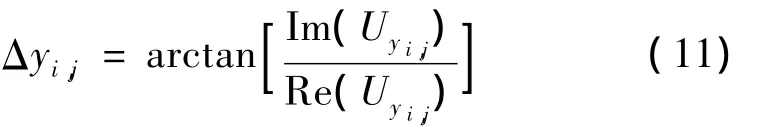
将(10)式和(11)式代入(5)式中，通过DCT解包裹即可求出连续相位。

2 LSBLS算法的改进

尽管LSBLS方法可以有效地克服欠采样带来的麻烦，与传统最小二相位解包裹相比存在优势，但当欠采样非常严重时，就会导致LSBLS方法失效，真实相位而不能解出。

为解决现有的LSBLS方法的缺点，作者在现有的LSBLS方法的基础上进行改进。同样将剪切干涉的原理引入到相位解包裹中，在(5)式的基础上构建一个等效的 2 维复光场:

同样沿x方法作1pixel的平移，创建新的光场:

将两光场相除有:

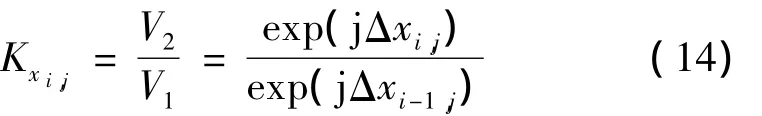
则:

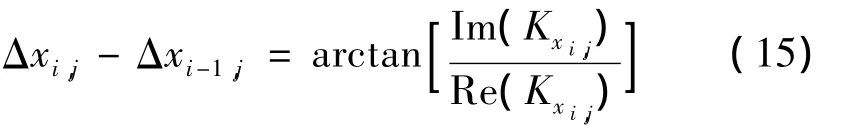
同理在y方向上有:

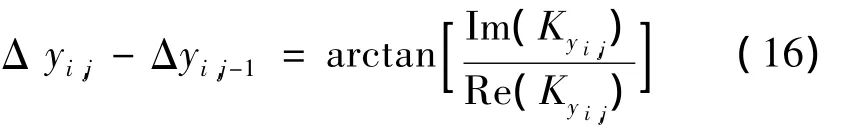
则(5)式变为:

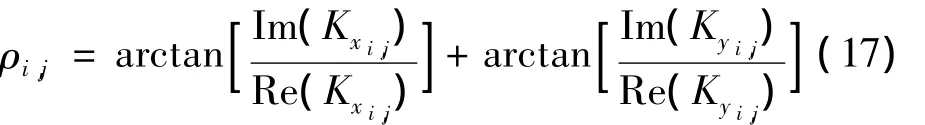
故用常规的求解泊松方程的方法即可求出连续相位。与原有的LSBLS算法相比，改进后的LSBLS算法并不会改变原有的LSBLS算法的计算量，在理论上，两种算法的计算时间是相同的。经过实验研究，作者发现改进后的LSBLS算法没有影响原有的LSBLS算法的计算时间，但在解决欠采样问题上，改进后的LSBLS算法有明显的优势。

尽管DCT能够满足常用的最小二乘相位解包裹，但是，当残差点较多时DCT非加权权最小二乘相位解包裹算法的计算结果比较平滑，从而有学者引入权重，抑制误差的传播，称为加权离散余弦变换(weighted discrete cosine transform，WDCT)。为补偿其平滑作用，采用加权来对最小二乘方法进行改进。权重定义

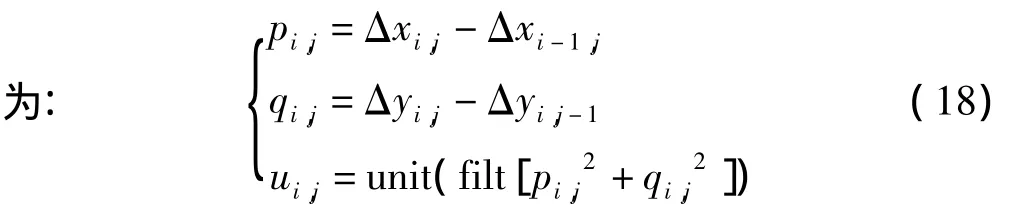
式中，pi，j和 qi，j分别为 x 方向和 y 方向相邻包裹相位差分之差，unit()为归一化处理，filt［］为均值滤波，求出权重 ui，j后，用 ui，j对 ρi，j进行加权处理:

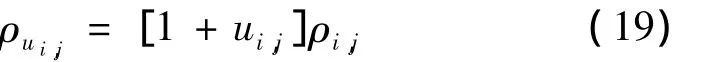
式中，ρui，j表示对 ρi，j加权处理的结果，然后利用(4)式泊松方程的求解即可求出连续相位。鉴于WDCT算法的优势，本文实验中采用WDCT算法解泊松方程。

3 实验与结果分析

为了验证本文中改进后的LSBLS方法的有效性，用MATLAB编程，以100倍的peaks函数构建一个2维相位分布(512pixel×512pixel)进行实验验证，该2维相位分布的相位最大值和相位最小值分布为-655.1120rad和810.6041rad。用LSBLS算法解该2维相位如图1所示。

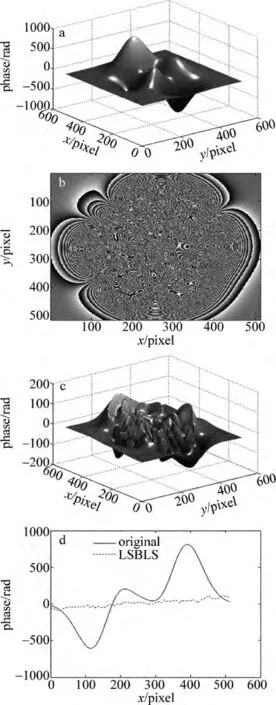
Fig.1 Results of unimproved LSBLSa—original phase b—wrapped phase c—unwrapped phase by LSBLS d—comparison between unwrapped phase by LSBLS and original phase

图1a是原始相位，图1b是原始包裹相位，图1c是用LSBLS算法解包裹的结果，图1c和图1a相比可以直观看出LSBLS解包裹误差很大，图1d是坐标y为256pixel时的切面轮廓图，从图1d可以看出，LSBLS解包裹误差极大。综合图1可以看出，LSBLS算法在原始相位变换太快时，欠采样带来的影响较为严重，相位解包裹失败。

下面采用本文中改进的LSBLS相位解包裹方法，为了对比，同样采用100倍的peaks函数进行实验，改进后的LSBLS算法解包裹实验如图2所示。

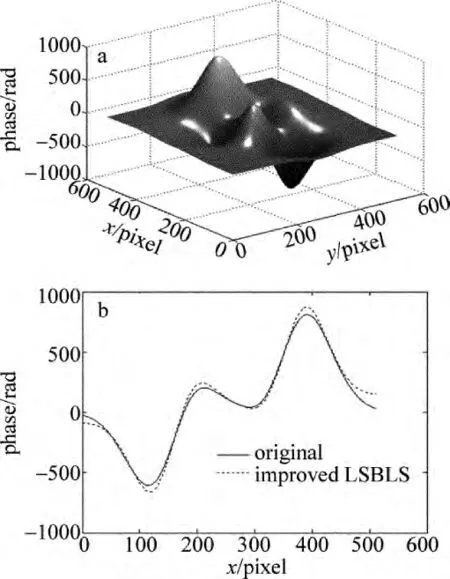
Fig.2 Results of improved LSBLSa—unwrapped phase by improved LSBLS b—comparison between unwrapped phase by improved LSBLS and original phase

从图2可以看出，改进后的LSBLS算法不仅能够解出其包裹相位，而且改进后的LSBLS算法误差较小。另外，改进后的LSBLS算法在运行时间上对原有的LSBLS算法运行时间没有影响，改进前后的LSBLS算法的运行时间都为3s左右。

在现实情况中由相移技术得到的包裹相位都存在一定的噪声，本文中根据现实情况对有噪声的包裹相位进行了研究，对有噪声的欠采样相位解包裹问题的研究如图3所示。

图3是对有噪声的包裹相位，通过窗口傅里叶滤波［16-18］后用改进的LSBLS方法解包裹的结果。图3c和图3d、图3b相比可以看出，原有的LSBLS算法解包裹失败了，而改进后的LSBLS算法能够还原原始相位。图3e是坐标x=256pixel时的剖面轮廓图，图3e更是明确地说明了改进后的LSBLS算法对欠采样较严重的包裹相位能够很好地解出真实相位。通过一系列的实验可知，本文中改进的LSBLS算法对欠采样问题的解决有较大的实用性。

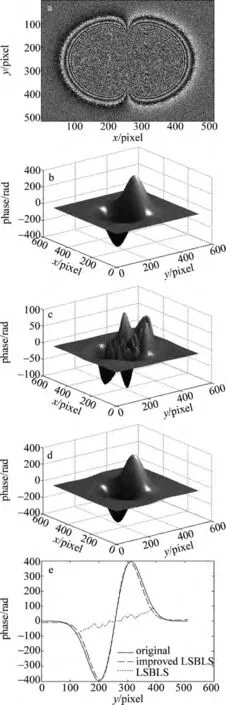
Fig.3 Results of phase unwrapping of the undersampling wrapped phase with noisea—wrapped phase with noise b—original phase c—unwrapped phase by LSBLS d—unwrapped phase by improved LSBLS e—comparison between two LSBLS algorithms and original phase

4 结论

相位变化太快而发生欠采样，导致不能顺利完成相位解包裹。欠采样问题一直是相位解包裹中的一个难点，尽管LSBLS算法有一定的抗欠采样能力，但当欠采样严重时，该算法同样不能得到满意的结果，甚至会解包裹失败。本文中依据现有的LSBLS算法，对LSBLS算法加以改进，并通过实验验证了改进后的LSBLS算法的正确性和有效性。

［1］ XU X，WANG K F，GU G Q，et al.Measurement of internal material flaws based on out-of-plane displacement digital speckle pattern interferometry［J］.Laser Technology，2012，36(4):548-552(in Chinese).

［2］ XIE M M，TAO B Q，JIANG J H.Nondestructive inspection technology based on grating big shearing digital speckle interference［J］.Laser Technology，2001，25(4):279-282(in Chinese).

［3］ ZHANG Y P，WANG K F.Application of LabVIEW and MATLAB in ESPI image processing［J］.Laser Technology，2009，33(6):582-589(in Chinese).

［4］ QIAN X F，RAO F，LI X H，et al.Accurate least-squares phase unwrapping algorithm［J］.Chinese Journal of Lasers，2012，39(2):0209001(in Chinese).

［5］ WEI Z Q，XU F，JIN Y Q.Phase unwrapping for SAR interferometry based on an ant colony optimization algorithm［J］.International Journal of Remote Sensing，2008，29(3):711-725.

［6］ QIAN X F，ZHANG Y A，LI X Y，et al.Phase unwrapping algorithm based on mask and least-squares iteration［J］.Acta Optica Sinica，2010，30(2):440-444(in Chinese).

［7］ GUO Y，CHEN X T.Study of improved phase unwrapping algorithm based on least squares［J］.Chinese Journal of Lasers，2014，41(5):0508005(in Chinese).

［8］ GHIGLIA D C，ROMERO L A.Robust two-dimensional weighted and unweighted phase unwrapping that uses fast transforms and iterative methods［J］.Journal of the Optical Society of America，1994，A11(1):107-117.

［9］ PRITT M D，SHIPMAN F S.Least-squares two-dimensional phase unwrapping using FFT’s［J］.IEEE Transactions on Geoscience and Remote Sensing，1994，32(3):706-708.

［10］ LIU J F，LI Y Q，LIU K.Weighted least-square phase unwrapping algorithm for noisy phase-map［J］.Acta Optica Sinica，2008，34(5):643-646(in Chinese).

［11］ DONG Ch M，LIU G L，YU Sh W，et al.An improved algorithm of weighted least squares for phase unwrapping［J］.Journal of Geodesy and Geodynamics，2011，31(s1):90-93(in Chinese).

［12］ FAN Q，YANG H R，LI G P，et al.Method for phase recovery from a single undersampled wrapped phase map［J］.Acta Optica Sinica，2011，31(3):0310002(in Chinese).

［13］ ZHANG X，QIAN X F.An improved on least-squares phase unwrapping algorithm for undersampled interferofram［J］.Acta Photonica Sinica，2011，40(1):121-125(in Chinese).

［14］ WANG H Y，ZHANG Z H，ZHAO B Q，et al.Unwrapping algorithm of under-sampled wrapped-phase map［J］.High Power Laser and Particle Beams，2012，24(10):2311-2317(in Chinese).

［15］ LI B，QIAN X F，LI X H，et al.Phase-unwrapping algorithm based on radial shearing principle［J］.Laser Technology，2013，37(1):44-47(in Chinese).

［16］ LI K，QIAN K M.Dynamic phase retrieval in temporal speckle pattern interferometry using least squares method and windowed Fourier filtering［J］.Optics Express，2011，19(19):18058-18066.

［17］ QIAN K M.Two-dimensional windowed Fourier transform for fringe pattern analysis:Principles，applications and implementations［J］.Optics and Lasers in Engineering ，2007，45(2):304-317.

［18］ QIAN K M.Windowed Fourier transform for fringe pattern analysis［J］.Applied Optics，2004，43(13):2695-2702.