基于热电制冷器温控系统数学建模和参量辨识

王选择，侯洪洋，翟中生，杨练根，刘文超

(1.湖北工业大学机械工程学院，武汉430068;2.湖北工业大学湖北省现代制造质量工程重点实验室，武汉430068)

引 言

在干涉测量中，半导体激光器(laser diode，LD)作为干涉测量系统的光源，半导体激光器的输出功率与波长等受温度的影响较大。一般温度变化1℃导致输出波长的改变为0.2nm～0.3nm，这会严重影响干涉测量误差，因此对半导体激光器温度控制很重要。目前一般采用半导体热电制冷器(thermoelectric cooler，TEC)作为温度控制执行元件，而常用温度控制的方法是用脉冲宽度调制技术控制TEC端电压和比例-积分-微分控制器［1-5］对热响应进行调整。但实验中发现TEC热惯性非常小，制冷制热速度很快，同时由TEC、温度传感器、模组(安装着激光二极管)和散热装置组成的实验系统［6-7］，温度传感的时间常数也很小，精度要求高，因此在温度控制之前，亟待需要解决的问题是建立合理的热分析数学模型，在此模型的基础上进行系统热响应分析，这对温度的预测和温度控制显得尤为重要。而对于装有激光二极管模组温度的实时监控，运用基于相差识别的温度传感原理［8］。

为了在实际运用中实现温度的有效控制。作者在建立温控系统热分析数学模型的基础上，重点研究了在输入电压恒定的条件下，基于TEC温控系统输入与输出特性，仿真［9］与实验验证此模型的合理性，并应用非线性曲线拟合最小二乘法对模型中的特性参量进行辨识。

1 实验装置

实验结构模块如图1所示，由散热片、TEC、模组构成，圆槽内嵌入激光二极管，带条纹的小方槽装上热敏电阻，分别检测散热片和模组温度，且模组上的小方槽与圆槽在同一高度，保证激光头和热敏电阻在同一温度梯度上。实验中使用QSI系列50mW，650nm激光二极管、CP系列12mm×12mm×3mm的TEC和表面贴装器件(surface mount decices，SMD)封装负温度系数热敏电阻。另外，激光二极管与模组连接处涂覆导热硅脂，热敏电阻［10］、模组、TEC、散热片连接处用导热绝缘的环氧树脂粘接固定。由于在上实际制造出的模组与TEC接触面尺寸大小相等，因此可以忽略TEC与环境的热交换及TEC与模组进行热传递的热损耗。

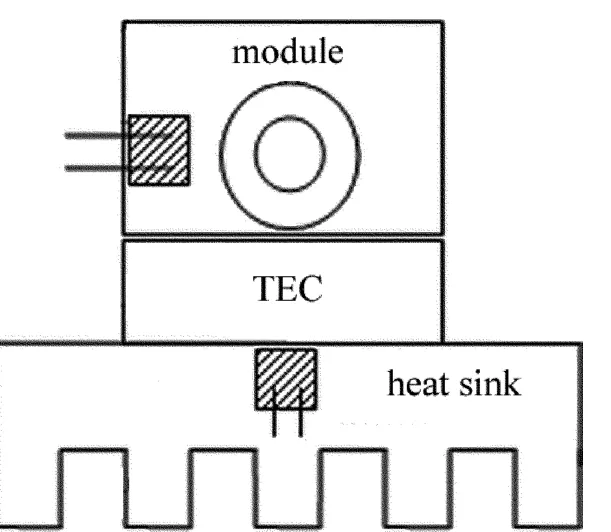
Fig.1 Structure module of experimental setup

2 实验系统数学模型的建立

2．1 热力学分析

TEC制冷制热原理利用了珀尔帖效应，将冷面的热量不断转移到热面。由能量守恒定律可知，从冷面失去的热能与热面得到的热能相等，因此系统的总热能可认为电流通过TEC内阻产生的内能。分别用Pr和Pc表示内阻热功率和转移热功率。此外在TEC对结构模块进行温度调节的同时，散热片与模组不断地与环境进行热能交换，主要为散热片释放到环境的热功率P1和装有激光二极管模组吸收到环境的热功率P4，分别满足如下关系:

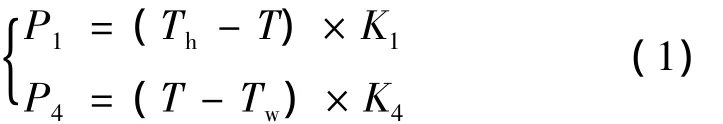
式中，Th为散热片温度，Tw为模组温度，T为环境温度，K1为散热片散热系数，K4为模组吸热系数。

在实际的温度测量中发现，TEC刚通电时，冷面和热面的温度变化得最快，随着冷热面温差的加大，热面温度的上升和冷面温度的下降都逐渐缓慢，由此可见，温差越大，阻止热量向冷面转移的能力越大，在温差达到最大时，TEC制冷功率为0，热量不再从冷面转移到热面，冷面温度不再下降。那么，用Pe表示抑制热能转移功率，它与冷热面温差ΔT关系为:

式中，Ke为温度抑制系数。

2．2 数学模型的建立

根据TEC热量的转移特性，可以认为内阻产生的热量Pr全部释放到TEC的热端面，为了能够清楚表达热传递的过程，建立了如图2所示的等效热传递模型，可以知道，散热片净热功率ΔP1和装有激光二极管模组的净热功率ΔP2满足关系如下:

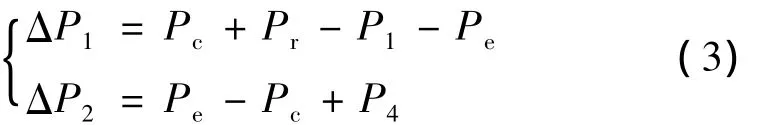
那么，散热片温度Th、模组温度Tw分别满足如下关系:

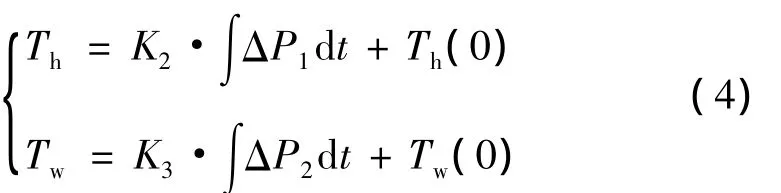
式中，K2，K3分别为散热片、模组的质量与其比热容的乘积的倒数，Th(0)，Tw(0)分别为散热片和模组的初始温度，t为时间变量。

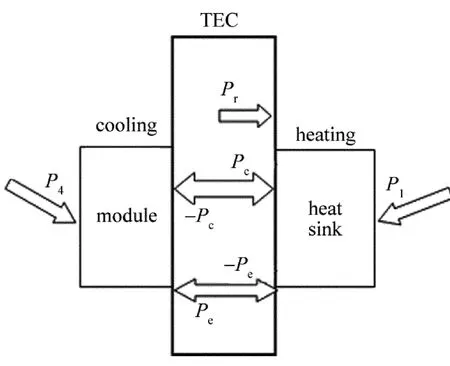
Fig.2 Equivalent model of heat transfer

Fig.3 Mathematical model of the system

依据以上分析，结合数学表达式和图2的等效热传递模型建立了系统数学模型，如图3所示。图中为积分环节，s为复变量。为了进行仿真分析和理论分析，使用阶跃信号作为系统输入，根据阶跃信号的特性，零时刻之前的系统阶跃响应没有意义，只有在零时刻之后，散热片和模组才具有初始温度，同时系统有了环境温度。

3 系统模型参量的确定

考虑到系统数学模型中参量太多，在进行参量辨识时，不能完全依靠求解整个系统最优来进行辨识，因此采用分步进行的方法。首先对系统的局部进行辨识，给出一个参量的范围值，然后在这个范围内寻找全系统最优值，保证所求的最优解稳定性好，能反映实际系统的传热过程。

3．1 特性参量 K1，K2，Ke，K3，K4 的确定

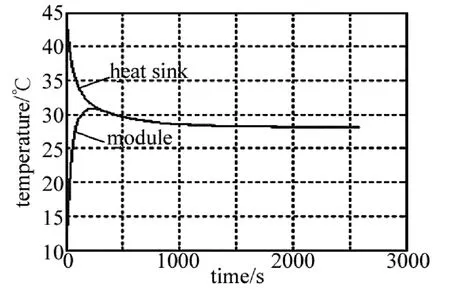
Fig.4 Temperature vs.time of K1，K2，Ke，K3，K4experiment

按照上述分步方案，首先进行了确定K1，K2，Ke，K3和K4参量的实验。先让TEC通电，调整通电方向，对装有激光二极管的模组制冷，检测到模组与散热片到达合适的温差后，让TEC断电。同时采集到散热片和模组温度特性曲线如图4所示，依据热力学定律，热量不断自发从热面转移到冷面，两者温度相等后，一起下降至室温。在TEC断电情况下，分析数学模型(见图3)，冷面转移到热面的热功率Pc和内阻产生的热功率Pr都为0，系统输入为单位阶跃信号，零时刻之后，散热片和模组才具有初始温度Th(0)，Tw(0)，同时系统有了环境温度T，输出为散热片温度Th，模组温度Tw。

在TEC断电的条件下，列出系统输入Xi与输出Xo的关系式:

分别消除 Xo，1，Xo，2可得单输出与单输入传递函数，在环境温度不变的条件下，认为系统输出为经过其传递函数，输入Xi为一常数阶跃响应，为了便于非线性曲线拟合，对其阶跃响应数学表达式进行归一化简化处理，输出可以表示为:

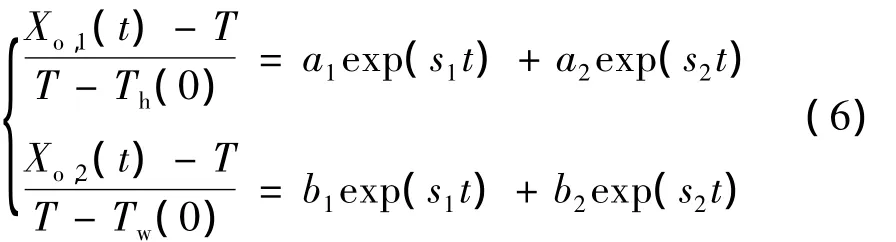
式中，s1和s2为方程s2+Es+F=0的根。E和F为方程系数。显然a1，a2不独立，且b1，b2也不独立，根据拉斯变换初值定理可知，a1+a2=-1，b1+b2=-1，同时它们满足如下的关系:

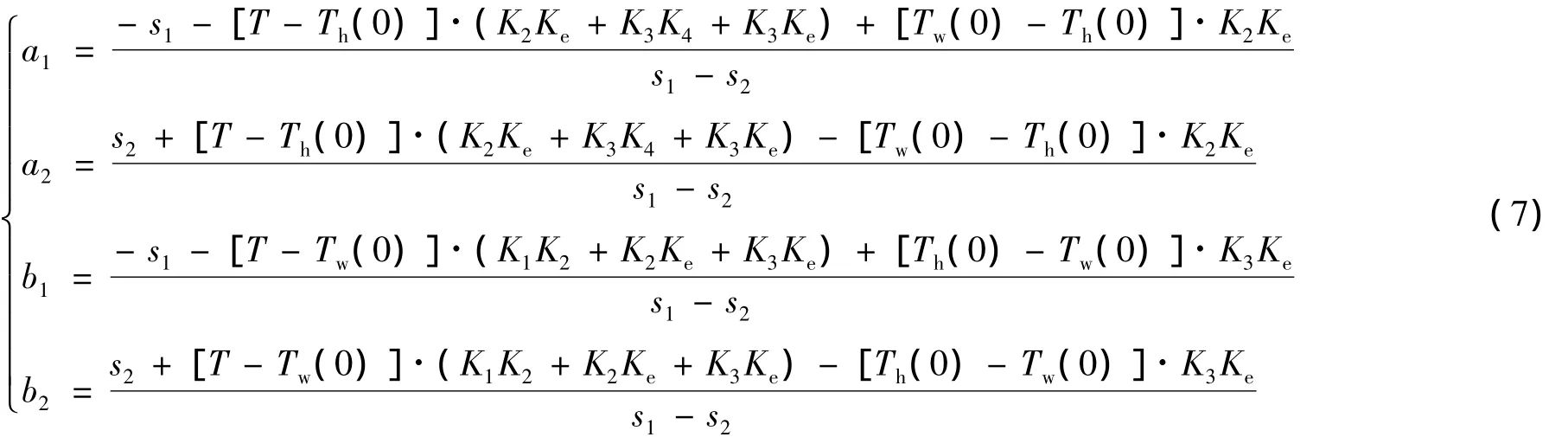
调用MATLAB的非线性最小二乘法曲线拟合函数，按照最小二乘法原理，要求实验曲线Xo，1与拟合曲线 Xo，1′满足如下关系:

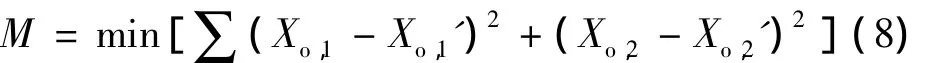
按照(6)式同时对模组和散热片数据进行归一化处理，也就是对 TEC 断电条件下的系统输出 Xo，1，Xo，2进行归一化处理。然后按照最小二乘法原理对归一化实验曲线进行特征辨识。拟合结果为:a1=-0.4339，a2=-0.5483，b1=0.4484，b2=-1.4744，s1=-0.0029，s2=-0.0170，归一化实验拟合曲线如图5所示。再将拟合的结果代入(7)式的4个方程，同时由(4)式可以知道，K3为模组质量与其比热容的乘积的倒数，且模组是为铝制材料，质量为2.9g，先确定K3=0.392的条件下，求解 K1，K2，Ke，K4这 4 个未知数:K1=0.021，K2=0.14169，Ke=0.0265，K4=0.0066。

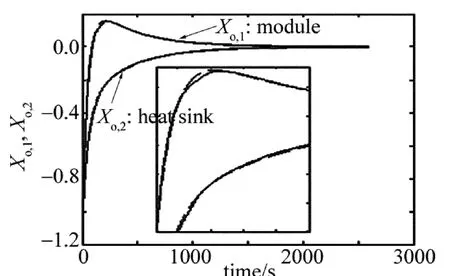
Fig.5 The normalized experimental curve and fitting curve of Xo

3．2 参量 Pr，Pc的确定

在确定了 K1，K2，Ke，K3，K4参量后，进行了优化参量Pr，Pc的实验。让TEC通电，对模组制冷，采集到装有激光二极管模组温度下降和散热片温度上升温度曲线，如图6所示。系统输入为单位阶跃信号，零时刻之后，散热片和模组初始温度为Th(0)，Tw(0)，系统环境温度为T，在环境温度不变的情况下，模组和散热片初始温度与环境温度相等，即T=Th(0)=Tw(0)，输出为散热片温度Th，模组温度Tw。根据图3中的数学模型列出系统输入Xi与输出Yo的关系:

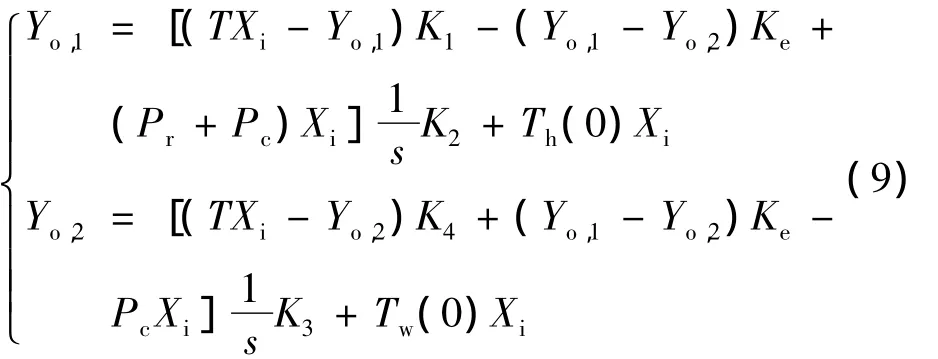
式中，Yo，1，Yo，2表示模组和散热片初始温差和环境温度相等、以及TEC通电条件下的系统输出。分别消除Yo，1，Yo，2，可得单输出与单输入传递函数 H1=Yo，1/Xi和H2=Yo，2/Xi，那么TEC通电条件下的阶跃响应为:

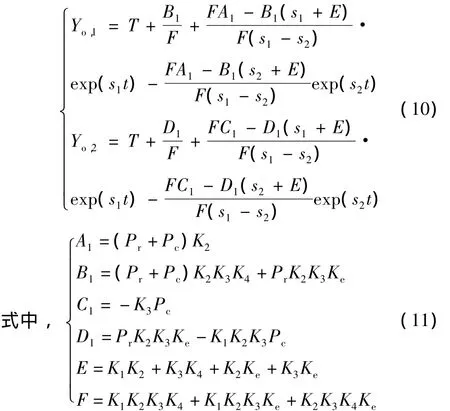
将 s1，s2，K1，K2，Ke，K3，K4代入(11)式，调用MATLAB的非线性曲线拟合 lsqcurvefit函数，按照(10)式对Pr和Pc进行特征辨识，要求拟合曲线Yo，1′，Yo，2′与实时曲线 Yo，1，Yo，2平方和最小，得到参量的值为:Pr=0.986W，Pc=1.3214W。最后用SIMULINK建立如图3所示的仿真模型，再用拟合参量值进行仿真，在MATLAB中分别用实线、长虚线、短虚线绘制了实验曲线、拟合曲线和仿真曲线，如图6所示。这3条曲线所反映的热电制冷器的制冷制热特性和规律是一致的，在冷面与热面温差最大时，TEC的制冷功率就小于抑制热能转移功率，模组温度开始上升，散热片温度跟随上升。

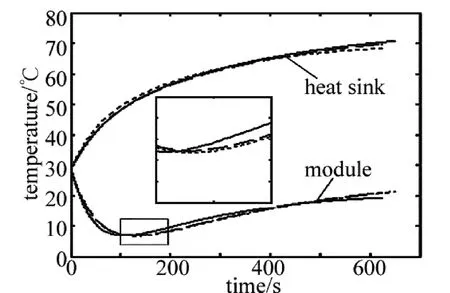
Fig.6 Temperature curve with experiment simulation and fitting of Pr，Pc experiment

4 结论

提出了半导体激光器温控系统结构模块的数学模型，运用时域分析的方法计算了模组和散热片的阶跃响应，对比数学模型的仿真分析，验证了模型仿真分析与理论分析的一致性，在基于相差识别温度采集系统基础上，利用非线性曲线拟合最小二乘法对数学模型的各个参量进行特征辨识，此方法为进一步半导体激光器温度控制奠定了基础。

［1］ GAO P D，ZHANG F Q.Design and implementation of high precision temperature control system for semiconductor lasers［J］.Laser Technology，2014，38(2):270-273(in Chinese).

［2］ CHEN W，YANG Zh，ZHANG W.Design of high precision laser temperature control circuit［J］ .Laser Technology，2014，38(5):669-674(in Chinese).

［3］ LIAO Zh Y，DENG H F，WU L H，et al.Design of high precision constant temperature control systems based on laser diodes［J］.Laser Technology，2012，36(6):771-775(in Chinese).

［4］ ZHANG Y N，TAN Y D，ZHANG Sh L.Temperature control system for frequency stabilization of total internal cavity microchip laser［J］.Infrared and Laser Engineering，2012，41(1):101-106(in Chinese).

［5］ YIN Zh Y，WANG Y F，LI G，et al.Design of high performance temperature controlling system based on TEC［J］.Computer Measurement＆ Control，2010，18(6):1296-1297(in Chinese).

［6］ AYAN R，AMITAVA B O，SANKAR D，et al.A simple scanning semiconductor diode laser source and its application in wavelength modulation spectroscopy around 825nm.［J］.Optics and Laser Technology，2007，39(2):359-367.

［7］ LIU Y，PAN H T，ZHAO Sh M，et al.Optimization design of structure of TEC temperature control system for microfluidic PCR［J］.Transducer and Microsystem Technologies，2013，32(9):85-88(in Chinese).

［8］ WANG X Z，ZENG Zh X，ZHONG Y N，et al.Precise measurement and control of temperature in semiconductor laser base on phase recognition［J］.Journal of Optoelectronics·Laser，2013，24(2):239-245(in Chinese).

［9］ CHENG X L，DENG Zh M.Simulation analysis of thermal smart structure for composite with TEC［J］.Computer Simulation，2008，25(4):16-21(in Chinese).

［10］ GUAN F W，LIU J，YU Sh M，et al.Clibration and R-T characteristics of NTC thermistor［J］.OME Information，2011，28(7):69-73(in Chinese).