表面张力对坡面薄层水流临界雷诺数的影响

孙三祥, 雷鹏帅, 张云霞, 武金明

(1.兰州交通大学 环境与市政工程学院, 甘肃 兰州 730070; 2.寒旱地区水资源综合利用教育部工程研究中心, 甘肃 兰州 730070)

表面张力对坡面薄层水流临界雷诺数的影响

孙三祥, 雷鹏帅, 张云霞, 武金明

(1.兰州交通大学 环境与市政工程学院, 甘肃 兰州 730070; 2.寒旱地区水资源综合利用教育部工程研究中心, 甘肃 兰州 730070)

资助项目：长江学者和创新团队发展计划项目“黄土坡地坡面流产沙过程及模拟”(IRT0966)

第一作者：孙三祥(1965—)，男(汉族)，甘肃省秦安县人，硕士，教授,主要从事土壤水力侵蚀方面的研究。E-mail:sunsanxiang@mail.lzjtu.cn。

摘要：[目的] 探究坡面薄层水流流态判别时表面张力的作用。[方法]采用比较作用力大小的理论方法。在比较表面张力(未降雨条件下)在运动方向上的所体现的表面波阻力与黏滞力大小的基础上，基于相关文献试验及数值模拟结果，分析波长、波高与水深的定量关系。[结果] (1) 层紊流判别临界雷诺数与弗劳德数、滚波波长、波高有关。 (2) 滚波发生条件(Fspan≥2)，坡面薄层水流临界雷诺数大于明渠水流临界雷诺数。[结论] 滚波发生后坡面薄层水流临界雷诺数最大值为明渠水流的1.187 5倍。

关键词：坡面薄层水流; 表面张力; 雷诺数; 弗劳德数; 滚波

层紊流流态是坡面薄层水流最基本的水动力学特性之一，它对坡面流的径流计算和输沙演算有直接影响[1]。坡面薄层水流层紊流流态的判别，一般直接借鉴明渠水流的临界雷诺数为标准，根据上、下临界雷诺数将流态依次分为层流、过渡流和紊流3种。明渠水流下临界(层流)雷诺数为500。但坡面薄层水流临界雷诺数的大小，国内外学者的看法并不是很一致。姚文艺、Emmett，Yoon[2]试验资料表明，下临界雷诺数为900(降雨条件下为800)，上临界雷诺数为2 000。吴长文、王礼先[3]认为在降雨条件下自然坡面薄层水流保持层流的条件是不存在的。Woolhiser等[4]采用运动波模型对牧场小流域的多次暴雨资料分析表明，坡面流流态可能是层流。Selby[4]认为坡面薄层水流是层流与紊流的混合。坡面薄层水流流态的分歧点大多集中在对其“层流”的界定上[5]。其雷诺数目前均采用明渠水流公式，按照平均水深计算。另外，与明渠水流不同，在一定临界水力条件下，坡面薄层水流会以“滚波”形式沿坡向下运动[6]。Dressler[7]认为谢才公式中的无量纲阻力系数达到床面比降的1/4形成滚波。根据水波理论[8]，滚波发生的条件是弗劳德数Fr≥2。滚波的演化由3个阶段组成[7]： (1) 初始的小振幅阶段，波周期基本不变； (2) 过渡阶段，波周期开始增加和出现波的聚合过程； (3) 最后阶段，发生显著的聚合现象，可以是小波聚合大波，也可以是大波吞并小波；同时，波周期也随着波高的增加而增加。

鉴于国内外学者对坡面薄层水流临界雷诺数的大小的看法不一致，进一步分析探讨非常必要。目前对于坡面流层、紊流流态的判别，主要基于试验观测，有必要从理论上予以分析。本研究通过表面波阻力与黏滞力大小的比较，基于相关文献试验资料，分析未降雨条件下表面张力对坡面薄层水流临界雷诺数的影响。

1表面张力作用

水工模型试验要求，若水深小于1.5 cm，必须考虑表面张力作用[9]。坡面薄层水流水深小，水流表面张力的作用不能忽略。表面张力与黏滞力属于阻滞流态运动的力，试验结果也表明，相同雷诺数条件下，坡面薄层水流阻力比明渠水流大[2]。因此可认为坡面薄层水流临界雷诺数应该大于500，其力学作用机理可以从表面张力与黏滞力之比来分析。

基于表面波(毛细波)运动特性，考虑表面张力作用，运用波动理论所得坡面流表面张力在运动方向上的力—表面波阻力为[10-11]：

(1)

式中：ρ——水体密度(kg/m3)；g——重力加速度(m/s2)；a——波幅(m)；B——过水断面宽度(m)。

明渠水流无量纲数雷诺数Re是水流的惯性力与黏滞力的比值，其计算式为：

(2)

式中：u——断面平均流速(m/min)；h——坡面平均水深(m)；v——水流的运动黏性系数(m2/s)。

弗劳德数Fr反映了水流的惯性力和重力之比。其计算式为：

(3)

表面波阻力与黏滞力之比为：

(4)

考虑B>>h， χ≈B，

式中：χ——湿周(m)； λ——波长(m)。

波幅为滚波峰值水深与平均水深的差值。试验中水深和波高采用数显测针(精度为0.01mm)测定。

式中：q——单宽流量(m2/s)。

式中：k——滚波数。

滚波数采用目测法，即单位时间内(1min)通过断面的滚波数量[12]。

2试验资料分析

2.1　室内模拟降雨试验

潘成忠等[12]通过上方来水和模拟降雨相结合的方法，研究了不同坡度和流量条件下滚波的参数变化。试验结果表明，在未降雨条件下，当流量分别为5和15L/min·m，坡度1.5°，3°，6°，9°，12°和15°(即2.6%～25.9%)时，波幅与水深之比为1∶1.7～1∶1。其具体试验条件为，针头式降雨器，降雨高度为5m,降雨均匀度大于85%。变坡式玻璃水槽底部铺设水砂纸以使床面接近裸土表面,水槽尺寸5m×1m×0.25m(长×宽×高)，来水经过二次稳流后进入试验水槽。水深和波高采用重庆水文仪器厂生产的数显测针(精度为0.01mm)测定。波高为滚波峰值水深与平均水深的差值。

降雨使断面滚波数显著增大,但其对波高和波长均无显著影响。说明降雨触发更多的滚波产生，而对其形状影响较小。

2.2　数值模拟

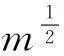
h′=h﹝1+0.005 sin(πt)﹞,Fr=3.71

模拟结果表明，起始区段，滚波形态发育不完全，波幅逐渐增大，流经30 m距离后，滚波形态发育完全，波幅与水深比为1∶1。表明定床和动床模拟过程中，滚波发育过程均经历了Brock所描述的3个阶段。在滚波形成及过渡阶段，动床较定床滚波初始小振幅阶段振动过渡过程更长，振幅更不规律；在滚波充分发展阶段，虽然动床床面的冲淤厚度较大，但滚波运动特性与定床情况类似(波数、最大水深相同或接近)。

2.3　室内定床放水试验

研究者[13-14]在坡度为3°，5°，10°时，采用放水试验，通过绘制lg(hf)与lg(v)的曲线来反映下临界雷诺数的值。得出的坡面薄层水流下临界雷诺数值约为700。具体试验条件为，恒定水流，下垫面为PVC塑料板(5 mm厚)，未加糙。床面尺寸8 m(长)×0.3 m(宽)×0.2 m(高)。用体积法测流量，根据床面宽确定平均水深采用，同时采用精度为0.01 mm的SX40-1测针测量水深，以相互校正。温度计测水温。

3分析讨论

3.1　未发生滚波

水深小于1.5 cm，波速小于23 cm/s，波长小于1.72 cm，为短波，根据定义，其波长与水深之比λ/h≤2.5[9]。

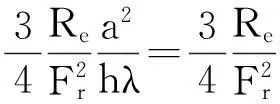
(5)

即坡面薄层流下临界雷诺数与的弗劳德数有关。

3.2　发生滚波

根据公式(4)，为了体现表面张力的最大影响，即公式(4)有最大值，取波幅与水深比为1∶1，波长最小值等于波幅[8]。滚波发生的条件是弗劳德数Fr≥2[8]，则：

(6)

明渠水流临界雷诺数为500～575，根据公式(6)，滚波发生后坡面薄层流下临界雷诺数为594～683。

该结论与文献[2]试验结果(下临界雷诺数为900)有差距，与本研究测得临界雷诺数的值(约为700)较为接近。

4结 论

(1) 由于表面张力的影响，坡面薄层水流层紊流临界判别数大于明渠水流临界判别数。弗劳德数、滚波波长、波高影响层紊流判别临界雷诺数。

(2) 考虑表面张力的作用，基于坡面薄层水流滚波发生条件(Fr≥2)分析得出坡面薄层水流临界雷诺数最大值为明渠水流临界雷诺数1.187 5倍。与相关文献试验结果有差距，与本研究定床放水试验结果接近。

[参考文献]

[1]张永东,吴淑芳,冯浩，等.土壤侵蚀过程中坡面流水力学特性及侵蚀动力研究评述[J].土壤,2013,45(1):26-33.

[2]姚文艺,汤立群.水力侵蚀产沙过程及模拟[M].河南 郑州:黄河水利出版社,2001.

[3]邵学军,王虹,费祥俊.坡面薄层流的数值模拟及在坡面流侵蚀研究中的应用[J].水利学报,2002(5)：15-19.

[4]罗榕婷,张光辉,曹颖.坡面含沙水流水动力学特性研究进展[J].地理科学进展,2009,28(4):567-574.

[5]吴淑芳,吴普特,原立峰.坡面径流调控薄层水流水力学特性试验[J].农业工程学报,2010,26(3):14-19.

[6]刘俊娥,王占礼,袁殷，等.黄土坡面薄层流产流过程试验研究[J].干旱地区农业研究,2010,28(5):223-227.

[7]李侃禹,曹志先,刘青泉.可冲刷坡面滚波数值模拟研究[J].力学与实践,2009,31(1):24-28.

[8]陶明德,水波引论[M].上海:复旦大学出版社,1990.

[9]赵德志,李焱.水工模型试验关于表面张力影响的波速论证[J].水利学报,2004(4)：38-41.

[10]周光炯,严宗毅,许世雄,等.流体力学[M].北京:高等教育出版社,2000.

[11]孙三祥.考虑表面张力作用的坡面流运动方程[J].水力发电学报,2013,32(1):145-149.

[12]潘成忠,上官周平.降雨和坡度对坡面流水动力学参数的影响[J].应用基础与工程科学学报,2009,17(6):843-851.

[13]冯美娟.定床阻力坡面薄层水流水力特性研究[D].甘肃 兰州:兰州交通大学,2013.

[14]冯美娟,孙三祥,孙移汉，等.基于VOF法的坡面薄层流水力特性数值模拟[J].灌溉排水学报,2013,32(2):142-144.

Effects of Capillary Force on Critical Reynolds Number of Thin Sheet Flow on Slope Surface

SUN Sanxiang, LEI Pengshuai, ZHANG Yunxia, WU Jinming

(1.SchoolofEnvironmentalandMunicipalEngineering,LanzhouJiaotongUniversity,Lanzhou,Gansu730070,China; 2.EngineeringResearchCenterforColdandAridRegionsWaterResourceComprehensiveUtilization,MinistryofEducation,Lanzhou,Gansu730070,China)

Abstract：[Objective] For studing the function of surface tension which be used for distinguishing laminar flow or turbulent flow of thin sheet flow on slope surface. [Methods] The theoretical method of comparing acting force was adopted. Upon the basis of comparison between resistance of surface waves which embodies the surface tension(no rain) in the direction of motion, and viscous force, the quantitative relationships among wave length, wave height and depth of water were analyzed with reference to the data from test and numerical simulation results in the related literatures. [Results] (1) The critical Reynolds number used to distinguishing laminar flow or turbulent flow depended on Froude number(Fspan), roll wave length and wave height; (2) In roll wave occurrence condition (Fspan≥2), the critical Reynolds number of thin sheet flow on slope surface was bigger than open channel flow. [Conclusion] The maximum of critical Reynolds number of the thin sheet flow on slope surface after roll wave occurred was 1.187 5 times of the corresponding value of open channel.

Keywords:thin sheet flow on slope surface; surface tension; Reynolds number; Froude number; roll wave

文献标识码：A

文章编号：1000-288X(2015)02-0179-03

中图分类号：U455.4

收稿日期：2014-10-18修回日期：2014-12-26