考虑空域分布多尺度信息熵的SAR 图像模板匹配*

张东兴，陈金来，赵培洪

(海军蚌埠士官学校 信息技术系，安徽 蚌埠233000)

1 引 言

合成孔径雷达(Synthetic Aperture Radar，SAR)图像匹配是把不同成像条件下对同一场景录取的两幅或多幅SAR 图像在空间上进行对准，以确定图像之间的平移、旋转和缩放等关系的过程［1－4］。SAR 图像匹配有广泛的应用，包括飞行器的景象匹配导航、目标跟踪、SAR 图像融合、变化检测和目标识别［5－6］等。

SAR 图像匹配可以分为基于灰度的匹配［7－8］和基于特征的匹配［9－11］:基于灰度的匹配将图像看作二维信号，采用统计的方法建立某种相似性度量，如相关函数、差平方和、差绝对值等，以判定相似性;基于特征的匹配是分别提取图像的特征，如点、线，区域等，对该特征进行描述，并通过特征描述的参数建立匹配关系。SAR 图像一般含有较多的相干斑噪声，且不同的成像条件下的图像几何结构变化较大［12］，因此SAR 图像对匹配算法的抗噪声和抗畸变的要求较高。不同的SAR 图像匹配算法有其各自适用的图像类型和应用，一般而言很难找到比较通用的算法。

自从香农将熵的概念引入信息论中以来［13］，熵已经在信号和图像处理等领域被广泛应用［14－15］。近年来，基于最大互信息的图像匹配方法得到了广泛研究［16］。互信息反映了两图像之间的统计相关性，一般用图像熵定量描述互信息。这种匹配方法不需要对图像进行预处理，而且可用于多种图像的自动化匹配，但研究表明这种算法计算量大、耗时长，且容易出现局部极值而造成误匹配。图像熵仅反映图像像素点值的数目，文献［17］给出了一种基于单元信息熵矢量的匹配算法以解决熵相同但形状不同的图像之间的区别问题;文献［18］给出了一种基于多尺度熵(Multi－Scale Entropy，MSE)的匹配跟踪算法，通过改变尺度因子得到一个多尺度信息熵矢量，利用矢量间的距离进行匹配，噪声会直接改变图像的灰度进而影响信息熵，仿真表明该算法易受噪声的影响而产生误配。尽管多尺度熵考虑了像素值在灰度空间的分散情况，但如果将图像的像素位置打乱，其多尺度熵仍然不变，即熵和多尺度熵都没有考虑像素空域分布的信息。因此，本文引入空域分布多尺度信息熵(Spatial Distribution MSE，SDMSE)的概念，对模板图像和各基准子图的各列或行求取多尺度熵，进而得到SDMSE 矩阵。通过求矩阵之间的相似系数来获取相似性度量，相似系数最大的位置对应匹配点。仿真表明本文算法的抗噪性能相对基于熵和多尺度熵的匹配方法有大幅的提高。

2 图像熵及多尺度熵

根据香农信息论，熵是表征事物存在或运动过程的不确定性的度量。对一个随机矢量R 来说，熵H(R)定义为

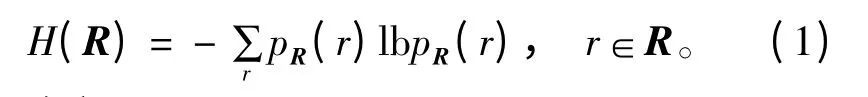
式中，pR(r)是随机矢量R 中元素r 的概率分布函数。一般而言，熵可以用来表征某消息的信息量，熵越大信息量越大。为将熵的概念引入图像匹配，需要先定义图像的熵，设图像像素的灰度共有s 级，图像的熵可以定义为

设图像是尺寸为m×n 个像素，第k 个灰度出现的次数为ck，则有

从式(2)看，熵的值取决于像素灰度值的概率分布函数。对一副给定的图像，式(3)中的m×n 是定值，pk仅取决于ck，ck为第k 个灰度像素的出现次数，也即任意两个灰度的像素只要其出现次数一样，其对熵的贡献是一样的，而无视它们在灰度空间的差异。

文献［19］给出了一种多尺度熵的算法，对长度为n 的一维离散信号(图像各列首尾相接可以得到一维信号)按照下式重新构建X 得到序列

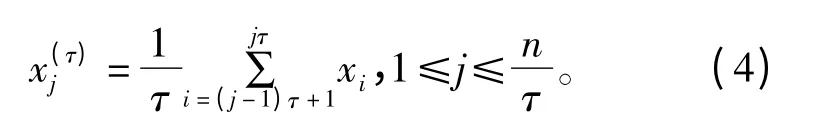
式中，τ 为尺度因子，也即熵统计每个灰度级的像素个数，多尺度熵则要统计每τ 个灰度级的像素个数。j=1，2，…，round(n/τ)，round(·)为向上求整操作。对Xτ序列按照式(2)求熵值H(τ)，随着τ 的变化将得到一系列熵值，这一系列熵值组成的序列即为X 的多尺度熵En={H(1)，H(2)，H(3)，…，H(τ)，…，H(256)}。当τ=1 时，H(τ)=H;随着τ 变大H(τ)在减小，当τ=256 时，H(τ)=0。在实际计算图像的多尺度熵时，为避免计算量太大，一般只选少数几个τ 值来组成多尺度熵，根据文献［18］的建议τ 分别为1、2、8、16 来构建图像多尺度熵。

不同灰度的像素对熵的贡献取决于像素出现个数而无视其在灰度空间差异，而多尺度熵的缺陷在于将像素位置打乱，其多尺度熵仍然一样，即没有考虑像素在空域的分布信息。鉴于此，本文给出一种考虑像素空域分布的多尺度信息熵以更完整地描述图像所蕴含的信息，用以匹配时得到更好的抗噪声性能。

3 图像空域分布多尺度信息熵及匹配

一个尺寸为m×n 个像素的图像，可以用矩阵的形式表示为

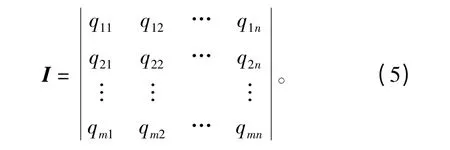
式中，qi，j为位于第i 行、第j 列的像素。要考虑像素空域分布的多尺度信息，可以对图像的行、列或某区域逐个进行多尺度熵的计算。这里以列为例，对图像的第j 列［q1j，q2j，...，qmj］T按照式(4)计算得到尺 度 τ 下 的 序 列其 中 k =round(m/τ)，j =1，2，…，n。使τ 变化r 个值，可以得到第j 列向量的r 个尺度的熵向量，对所有列求多尺度熵可以得到一个r×n 的熵矩阵。

熵用于图像模板匹配需要在基准图像中对各个位置的基准子图计算熵，并度量两者之间的相似性。熵是标量，可以通过差的绝对值来建立相似性度量，差越小越相似;多尺度熵是矢量，可以用矢量间的欧式距离来建立相似度量，距离越小越相似。图像的空域分布多尺度熵是一个矩阵，因此需要度量矩阵之间的相似性，本文采用求相关的方法来度量两矩阵之间的相似度。设两图像的SDMSE 矩阵为M1、M2，将两矩阵的各列分别进行首尾相连得到两个向量m1、m2，利用下式进行相关系数c 的求解:

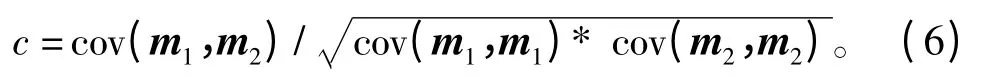
式中，cov 表示求协方差运算。c 越大表示两矩阵的相关性越强，也即两矩阵越相似。式(6)计算得出的最大值对应匹配位置。

4 仿真与分析

对常见的三种图像噪声即泊松噪声、高斯噪声和椒盐噪声进行抗噪性对比实验。衡量一幅图像噪声的强弱需要用到信噪比(Signal to Noise Ratio，SNR)的概念，其大小取决于图像信号功率和图像噪声功率之比，即

式中，ps和pn分别是信号和噪声的功率。若匹配误差小于10 个像素为正确匹配的话，本文将实时图可以正确匹配的最小信噪比叫作临界信噪比。为验证本文算法的性能，使用不同的SAR 图像进行模板匹配仿真。为减少计算量，选取4 个尺度来构建图像多尺度熵矢量。实验数据和结果是在处理器为奔腾双核2 GHz、内存为2 GB的电脑、运行软件为MATLAB R2010a 的条件下获得。

4.1 仿真一

本仿真对基于熵、多尺度熵和SDMSE 的SAR图像匹配算法，从计算时间和抗噪声性能两方面进行对比。使用的图像如图1所示，图2是匹配效果，表1是实验数据。

图1 仿真一中用的基准图和模板图Fig.1 The images used in the template matching in Simulation 1

图2 仿真一的匹配相关面Fig.2 Correlation surface in Simulation 1

表1 三种算法的抗噪声性能对比Table 1 The anti－noise performance of three algorithms

仿真表明三种算法对无噪声的图像都可以正确匹配，相对而言SDMSE 的计算时间大幅增加。从表1可以看出:

(1)采用熵和多尺度熵的匹配，受泊松噪声(泊松噪声取决于图像本身)影响，匹配误差太大，可认为匹配失败，而本文算法则可以正确匹配;

(2)受高斯噪声影响，采用熵和多尺度熵的匹配在信噪比分别大于44.03 dB和34.78 dB情况下才可以正确匹配，而SDMSE 在6.7 dB的信噪比情况下就可以做到正确匹配;

(3)在椒盐噪声的干扰下，基于熵和多尺度熵的匹配算法要在更大的信噪比(50 dB以上)才可以得到正确匹配，SDMSE 在15 dB左右即可得到无误差匹配。

4.2 仿真二

从仿真一可以看出SDMSE 匹配算法可以获得较好的抗噪声性能，但计算时间大幅增加。为减少计算量，在尺度个数分别为4、3、2、1 的情况下进行计算匹配时间和抗噪性能的对比。当尺度个数为1时，没有体现出多尺度，严格来讲不是SDMSE，为了对比也将该种情况进行仿真，图3给出了匹配所用图像，图4是匹配效果图，实验数据如表2所示。

图3 仿真二中用的基准图和模板图Fig.3 The images used in the template matching in Simulation 2

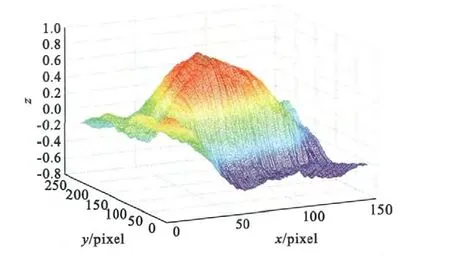
图4 仿真二的匹配相关面Fig.4 Correlation surface in Simulation 2

表2 尺度个数对匹配性能的影响Table 2 Experimental data of the four algorithms

从表2可以看出，随着尺度个数的减少，平均计算时间递减，其中尺度个数为4、3、2 时，平均计算时间相差几十秒，但尺度个数由2 变为1 时，计算时间减少了160 多秒，减幅较大。尺度个数由4 变为1，计算时间减少了40%。如何折衷抗噪性能的降低和计算时间的减小需要视情况而定。从抗噪性能来看，表中四种情况都对泊松噪声有很好的适用性，可以无误差匹配。随着尺度个数的减少，SDMSE 匹配算法对高斯噪声和椒盐噪声的适应性依然很强，因此，在信噪比允许的情况下可以考虑选用尺度个数较少的SDMSE 算法以节省运算时间。

5 结束语

图像的熵和多尺度熵只考虑了像素在灰度空间的情况，而无视像素的位置信息，因此本文考虑像素空域分布，给出一种空域分布多尺度信息熵(SDMSE)以更准确地描述图像信息。对图像的每一列计算多尺度熵，各列的多尺度熵组成一个多尺度熵矩阵。仿真结果表明，SDMSE 相比熵和多尺度熵具有更好的抗噪声性能，因为图像噪声是普遍存在而且会直接影响像素和熵的值，所以本文算法有一定的应用价值。减小尺度的个数会使抗噪性能略有降低，但可以减小计算量，如何折衷两者可以视具体情况而定。

本文算法虽然抗噪声性能优异，但计算量较大。在减少计算量方面，本文仿真二也进行了探索，虽然一定程度上降低了计算量，但计算时间仍然较长。如何在不降低抗噪性能的情况下进一步减小计算量是一个有待研究的问题。

［1］ 孙仲康，沈振康. 数字图像处理及其应用［M］. 北京:国防工业出版社，1986:233－235，307－309.SUN Zhongkang，SHEN Zhenkang.Digital Image Processing and Its Applications［M］. Beijing:National Defense Industry Press，1986:233－235，307－309.(in Chinese)

［2］ 贺柏根，朱明.改进的抗全仿射尺度不变特征变换图像匹配算法［J］.光学精密工程，2011，10(19):2472－2477.HE Baigen，ZHU Ming.Improved fully affine invariant SIFT－based image matching algorithm［J］.Optics and Precision Engineering，2011，10(19):2472－2477.(in Chinese)

［3］ 邱建国，张建国，李凯. 基于Harris 与Sift 算法的图像匹配方法［J］.测试技术学报，2009，23(3):271－274.QIU Jianguo，ZHANG Jianguo，LI Kai. An Images Matching Method Base on Harris and Sift Algorithm［J］.Journal of Test and Measurement Technology，2009，23(3):271－274.(in Chinese)

［4］ 李壮，雷志辉，于起峰.基于梯度径向夹角直方图的异源图像匹配［J］.测绘学报，2011，40(3):318－325.LI Zhuang，LEI Zhihui，YU Qifeng. MatchingMulti sensor Images Basedon Gradient Radius Angle Pyramid Histogram［J］.Acta Geodaetica et Cartographica Sinica，2011，40(3):318－325.(in Chinese)

［5］ 刘振，姜晖，徐海峰.基于二维非参数特征分析的SAR 图像目标识别［J］.电讯技术，2012，52(12):1940－1945.LIU Zhen，JIANG Hui，XU Haifeng. SAR Image Target Recognition Based on Two Dimensional Nonparametric Feature Analysis［J］. Telecommunication Engineering，2012，52(12):1940－1945.(in Chinese)

［6］ 何峻，赵宏钟，付强.自动目标识别性能评估指标简述［J］.电讯技术，2007，47(5):32－37.HE Jun，ZHAO Hongzhong，FU Qiang. A Survey of Measures on ATR Performance Evaluation［J］.Telecommunication Engineering，2007，47(5):32－37.(in Chinese)

［7］ 张慧慧，林伟，吕全义.基于线特征直方图的SAR 图像预匹配算法［J］.计算机科学，2013，40(4):266－269.ZHANG Huihui，LIN Wei，LYU Quanyi. SAR Image Matching Pretreatment Algorithm Based on Line Feature Histogram，Computer Science，2013，40(4):266－269.(in Chinese)

［8］ 李强，张钹.一种基于图像灰度的快速匹配算法［J］.软件学报，2006，17(2):216－222.LI Qiang，ZHANG Bo. A Fast Matching Algorithm Based on Image Gray Value［J］. Journal of Software，2006，17(2):216－222.(in Chinese)

［9］ Huang Yang，Liu Jinshuo，Tu Meisheng，et al.Research on CUDA－ based SIFT Registration of SAR Image ［C］//Proceedings of the 2011 Fourth International Symposium on PAAP.Tianjin:IEEE，2011:100－104.

［10］ Bellavia F，Tegolo D，Valenti C.Improving Harris corner selection strategy［J］. IET Computer Vision，2011，5(2):87－96.

［11］ Liu Zhaoxia，An Jubai，Jing Yu. A Simple and Robust Feature Point Matching Algorithm Based on Restricted Spatial Order Constraints for Aerial Image Registration［J］. IEEE Geosciences and Remote Sensing Society，2012，50(2):514－527.

［12］ 王光新，林有明，张送保. SAR 图像数据稀疏性分析及在特征增强中的应用［J］. 计算机科学，2011，38(2):267－270.WANG Guangxin，LIN Youming，ZHANG Songbao.Sparsity of SAR Image with Application to Feature Enhancement［J］. Computer Science，2011，38(2):267－270.(in Chinese)

［13］ 荆仁杰，叶秀清，徐胜荣，等. 计算机图像处理［M］.杭州:浙江大学出版社，1992.JING Renjie，YE Xiuqing，XU Shengrong，et al.Computer image processing［M］.Hangzhou:Zhejiang University Press，1992(in Chinese)

［14］ Shiozak I A.Edge extraction using entropy operator［J］.CV GIP Proceedings，1986，36(1):1－9.

［15］ Pal N R，Pal S K.Object2 background segmentation using new definitions of entropy［J］.IEEE Proceedings E－Computers and Digital Techniques，1989:136(4):284－295.

［16］ 魏雪丽，张桦，马艳洁，等.基于最大互信息的图像拼接优化算法［J］.光电子·激光，2009，20(10):1399－1402.WEI Xueli，ZHANG Hua，MA Yanjie，et al.Image mosaic optimization algorithm Based on the maximum mutual information ［J］. Journal of Optoelectronics·Laser，2009，20(10):1399－1402.(in Chinese)

［17］ 江和平，沈振康.基于单元信息熵矢量特征的图像匹配跟踪算法［J］.信号处理，2006，22(5):678－682.JIANG Heping，SHEN Zhenkang.Image Matching Tracking Algorithm Based on the Unit－entropy Vector Feature［J］.Signal Processing，2006，22(5):678－682.(in Chinese)

［18］ 刘兴淼，王仕成，赵静.基于图像多尺度熵的红外图像匹配跟踪算法［J］.控制与决策，2011，26(5):768－772.LIU Xingmiao，WANG Shicheng，ZHAO Jing. Infrared image matching tracking algorithm based on image multi－scale entropy［J］.Control and Decision，2011，26(5):768－772(in Chinese)

［19］ Costam，Goldberger A L，Peng C K.Multiscale entropy analysis of complex physiologic time series［J］. Physical Review Letters，2002，89(5):1－4.