LTE－A 上行链路中单用户MIMO 的球形译码算法性能分析*

张 源，沈 皓，赵 昆，夏 斌

(1.上海贝尔股份有限公司，上海201206;2.上海交通大学 电子工程系，上海200240)

1 引 言

长期演进方案(Long－Term Evolution，LTE)是当前移动通信的主流技术标准之一，相比上一代的技术标准具有高速数据传输和低延迟等特性，其演进标准LTE－Advanced(LTE－A)正在推动着移动通信技术的进一步发展。多输入多输出(Multiple－input Multiple－output，MIMO)技术是LTE－A 的核心技术之一，能够为系统实现空间分集和空间复用等增益方式，其中空间复用的意义在于无需增加发送功率和带宽即可显著提高无线系统的容量和频谱效率。在MIMO 技术方面，LTE－A 中相对LTE 引入了一些增强。就上行链路而言，LTE 尚未支持单用户MIMO(Single－User MIMO，SU－MIMO)，LTE－A 则引入了对最大4 天线发送8 天线接收的SU－MIMO 的支持［1］，在空间复用的情形下对吞吐量有了大幅提升。在多址技术方面，正交频分多址(Orthogonal Frequency Division Multiple Access，OFDMA)和单载波频分多址(Single－Carrier FDMA，SCFDMA)分别为LTE－A 的下行和上行链路所采用。相比OFDMA，SC－FDMA 在保持正交性的同时实现了较低的峰均比(Peak－to－Average Power Ratio，PAPR)，从而简化了用户终端(User Equipment，UE)的实现。

接收端检测算法对于MIMO 系统的性能和复杂度具有重要影响，也是MIMO OFDMA 和MIMO SC－FDMA 技术的主要难点之一。空间复用使得MIMO 系统的发送端利用多个天线同时发送多个数据流，这些数据流的多个线性组合到达接收端的多个天线，从而引入数据流之间的干扰。对于空间复用MIMO 系统的检测算法，改进其性能和复杂度的权衡具有重要的意义，在文献中已有相当数量的研究。最大似然(Maximum Likelihood，ML)检测是理论上最优的检测算法，但因为实现的复杂度随天线数目和调制阶数呈指数增长而无法应用于实际系统。低复杂度的算法中，迫零(Zero Forcing，ZF)和最小均方误差(Minimum Mean Square Error，MMSE)都属于线性检测算法，虽然其复杂度相比ML 有很大的降低，但是性能不够理想，因而以ML 为基础的降低复杂度的算法同样受到关注。为了接近ML 的性能并显著地降低复杂度，文献［2］提出了球形译码(Sphere Decoding，SD)检测算法。这类算法的基本思想是，在一个以输出矢量为中心半径为某预设值的多维球内，搜索格点并找出最大似然点，其中格点集合由所有可能的输入矢量经过系统函数映射得到。因为搜索仅限于球内格点而不是所有格点，所以搜索的格点数相比ML 可以显著减少。初始半径的确定以及球内格点的搜索方法都直接影响到搜索的格点数，因而成为SD 算法的关键问题。

将SD 算法应用于MIMO 系统的信号检测最早由文献［3］提出，随后很多研究提出了SD 算法的针对特定系统的实现方案以及各种改进。文献［4］对文献［2］中深度优先的格点搜索方法进行了改进，并且在找到更近的有效格点时缩小半径，从而在保持性能的同时提升了搜索效率，降低了复杂度。相比基于深度优先搜索的SD 算法，一些广度优先的算法，如K－ best SD［5］和固定复杂度SD(Fixed－complexity SD，FSD)［6］分别通过设定搜索格点数目的上限和固定值来控制复杂度，从而更有利于硬件实现，但性能损失较为明显。对于SD 算法在MIMO OFDMA 系统中的应用也已经有相当数量的研究，如文献［7］针对SD 算法本身，文献［8］针对与之配合使用的相关方法。然而在MIMO SC－ FDMA 系统中，发送端相比MIMO OFDMA 系统增加了离散傅里叶变换(Discret Furier Transform，DFT)扩展的环节，使得接收端检测算法的设计变得更为复杂。作者在深入调研的基础上得知，现有文献中尚未充分涉及SD 算法在MIMO SC－FDMA 系统中的应用。与此相关的文献主要有文献［9－11］，分别对SD 算法考虑了不同的实现方案，并通过仿真对误码率(Bit Error Rate，BER)或误块率(Block Error Rate，BLER)进行了评估。然而现有文献中存在的一个共同问题是，所用的MIMO SC－FDMA 系统模型和仿真设置相比实际的LTE－A 上行链路尚有显著的差距，对于信道估计均采用理想的假定，因而对于在实际系统中应用SD 算法的参考意义有所不足;除此之外还有其他多种问题存在，例如文献［11］未指明具体采用何种SD 算法作为其实现方案的基础。为了分析SD 算法在实际的LTE－A 系统中的适用性，本文针对LTE－A 上行SU－MIMO 的应用场景，在遵循3GPP 标准的仿真平台中实现了SD 算法并进行了性能评估;所引入的实现方案不仅考虑了性能上与ML 的接近性，也考虑了在实际系统中的可实现性。从所得到的仿真结果出发，本文阐明了SD相对MMSE 的性能增益的存在，并分析了不同的调制编码方案(Modulation and Coding Scheme，MCS)和物理资源块(Physical Resource Block，PRB)数目等配置下该增益的相对强弱，从而初步明确了SD 算法的适用条件，为其工程实现提供了参考依据。

文中符号说明如下:(·)T表示矩阵的转置，(·)H表示矩阵的共轭转置，IN表示N×N 的单位矩阵，‖·‖表示矢量的欧氏范数。

2 系统模型

完整的LTE－A 上行链路包含多个模块，如发送端有Turbo 编码、速率匹配、DFT 扩展等，这些模块在接收端都有对应的部分。为简化描述，以下我们仅给出与接收端检测算法相关的数学表达式。令发送天线数为Nt，接收天线数为Nr。在发送端(UE侧)，已编码的比特序列经过QAM(包括QPSK、16QAM、64QAM)调制生成复值符号，所生成的QAM符号经过N 点DFT 扩展得到频率域信号，并被映射到M ＞N 个频率点。随后，这些频率点经过M 点IFFT 得到时间域信号，该时间域信号在添加循环前缀(Cyclic Prefix，CP)之后进行发送。

在接收端，接收信号经过移除CP，并经过M 点FFT 得到频率域信号。随后经过解资源映射，分别得到N 个子载波的信号。OFDM 符号中第n 个子载波的频率域信号可表示为

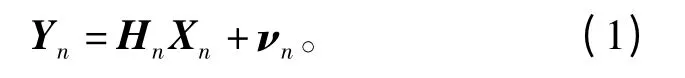
其中，Yn∈CNr×1是第n 个子载波的接收信号矢量，Hn∈CNr×Nt为第n 个子载波的频率域信道矩阵，Xn∈CNt×1为相应的频率域发送信号，νn∈CNr×1为相应的噪声。Xn与DFT 扩展之前的QAM 符号的关系可表示为

其中，FN∈CN×N为DFT 矩阵，xnt∈CN×1为第nt个发送天线的时间域信号，由N 个QAM 符号组成，其第k 个分量xnt(k)即为第k 个时刻的QAM 符号。接收端可以通过解调参考信号(Demodulation Reference Signal，DM－ RS)实现频率域的信道估计，Hn的估计值以及噪声方差的估计值被作为检测算法的输入参与对的求解。

3 算法实现方案

对于第2 节所述的系统模型，检测算法所要实现的目标是求解所对应比特的对数似然比(Log Likelihood Ratio，LLR)值，其输入包括Yn、以及。针对这一目标，SD 算法在系统中的实现需要考虑两个方面:一是选取何种SD 算法，二是将何种距离量度作为最小化的对象;前者决定了算法实现的内部流程，后者决定了算法实现的外部流程。出于对性能上与ML 的接近性以及在实际系统中的可实现性两方面的考量，本文采用文献［12］中的单树搜索SD 算法，并结合文献［11］中的迭代干扰消除流程，引入LTE－A 上行链路中SD 算法的实现方案。该实现方案由以下步骤描述:

(1)初始化:对n=1，2，…，N，计算Xn的MMSE解并经过IDFT 和解调得出QAM 符号矢量的估计此时视为SD算法的第0 次迭代;

在以上步骤中，距离量度的初始化(即初始半径的确定)与文献［12］的不同之处在于，参与距离量度计算的QAM 符号矢量是最近一次得到的而不是基于ZF 所得的结果。就算法实现而言，本文与文献［9］的主要区别在于通过迭代干扰消除将1 次NNt流的SD 求解转化为N 次Nt流的SD 求解，从而避免了高复杂度;与文献［10］的主要区别在于不依赖符号间干扰较弱的假设，并且对MMSE 算法未作修改;与文献［11］的主要区别在于结合了具体化的SD 算法，并选择了更易于实现的初始半径确定方法，避免了QR 分解的计算。

4 仿真结果与分析

本节给出第3 节所描述的SD 算法实现方案在LTE－ A 上行链路中的一些仿真结果。仿真采用3GPP 标准中规定的PUSCH 信号发送和接收流程(未配置控制信息的传输)，信道模型采用3GPP EPA 模型(反映低速运动的情形)。子帧结构方面采用正常CP，每个子帧内的14 个OFDM 符号中有12 个数据符号和2 个DM－ RS 符号，接收端通过DM－RS 实现信道估计。子载波的映射方式为集中式，总数目为2048 个。我们考虑三种不同的参数配置情形:MCS 10，5 个PRB，码率0.678 8(配置1);MCS 10，10 个PRB，码率0.666 7(配置2);MCS 20，5 个PRB，码率0.824 2(配置3)。配置1 和配置2采用QPSK，配置3 采用16QAM，从而便于观察不同调制阶数之间的对比。

图1给出了EPA 信道下2 发4 收，采用配置1的BER 仿真结果，图2给出了这一情形下的BLER仿真结果。从两幅图中都可以看出，当SNR 充分高时，采用SD 算法能够产生显著的相对MMSE 的增益。与此相反的是，当SNR 充分低时，MMSE 的性能则优于SD。对于高SNR 的性能增益可以解释为，SD 算法在本质上是降低复杂度的ML，因而在SNR 充分高时体现出相对MMSE 的优势。另一方面，SNR 充分低时由于MMSE 和ML 的性能差别不大，而SD 相对ML 的复杂度降低导致了相对此差别更明显的性能损失;具体地说，由于此时信道估计的效果不够好，使得初始解(MMSE 检测的结果)更加不准确，并且增强了干扰消除时的误差传播，因而导致SD 的性能有明显的损失，这就解释了低SNR 下MMSE 的优越性。然而实际系统通常需要满足较小的错误率上限的要求(如要求BLER 小于0.01)，此时SD 相对MMSE 已经有了较为可观的增益(如图2所反映的增益至少约1.4 dB)，因而使用SD 对于提升性能具有充分的意义。

图1 EPA 信道下2 发4 收，采用配置1 的误码率Fig.1 Bit error rate under EPA channel，with 2 transmit and 4 receive antennas，using configuration 1

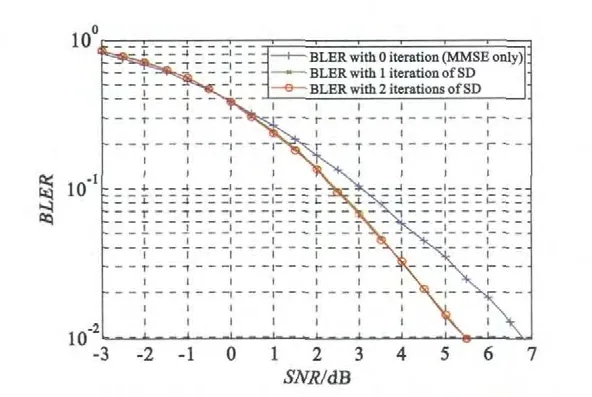
图2 EPA 信道下2 发4 收，采用配置1 的误块率Fig.2 Block error rate under EPA channel，with 2 transmit and 4 receive antennas，using configuration 1

为了比较不同配置下SD 相对MMSE 的增益大小，我们分别在图3和图4中给出了配置2 和配置3的BLER 仿真结果。考虑到错误率充分低时数值精确度可能不够好，我们选取BLER 为0.05 时的增益进行比较。通过图上测量得出，配置1、配置2 和配置3 中SD 相对MMSE 的增益分别为0.724 dB、0.71 dB和1.1 dB，可见配置3 的增益显著高于前两者。究其原因，首先配置3 有较高阶的调制，这使得ML(以及SD)相对MMSE 的增益较高;其次，较高的MCS 对应较高的工作SNR，从而信道估计的结果更加准确，亦导致增益的提高。由此可以认为，对于较高的MCS，SD 更能够体现出相对MMSE 的性能优势。

图3 EPA 信道下2 发4 收，采用配置2 的误块率Fig.3 Block error rate under EPA channel，with 2 transmit and 4 receive antennas，using configuration 2

图4 EPA 信道下2 发4 收，采用配置3 的误块率Fig.4 Block error rate under EPA channel，with 2 transmit and 4 receive antennas，using configuration 3

从图1和图2中还可以看出，将SD 算法进行二次迭代几乎不再有额外的增益，即二次迭代未能够改进BLER，甚至BER 也未见改进;与此类似，图3也表明二次迭代产生的额外增益较为微弱。而根据文献［11］中的结果，在无编码的情形下二次迭代能够产生显著的额外增益。两种情形的对比可以说明，信道编码的运用使得增加一次迭代能够产生的增益被显著地削弱。具体地说，无编码系统的性能取决于单个QAM 符号的解调结果，故只要改进部分比特的LLR 即能够显著地改进符号的解调结果;而有编码系统的性能取决于整个码块的译码结果，增加一次迭代可能改进了码块中部分比特的LLR，但是这些改进还不能够使得整个码块的译码结果得到充分的改进，从而无法像无编码系统那样通过增加一次SD 算法的迭代来充分提升性能。因而从经验的角度我们可以认为，SD 算法的二次迭代不适用于实际系统。

5 结束语

本文通过对现有文献中的SD 算法以及相关方法的分析，引入了一种针对LTE－A 上行链路的SD算法实现方案，并通过遵循3GPP 标准的仿真平台对其错误率性能进行了仿真。仿真结果验证了SD相对MMSE 的性能增益的存在，并揭示出不同的配置情形下该增益的相对强弱。分析发现，当SNR 充分高时采用SD 算法能够产生显著的相对MMSE 的增益，当调制阶数较高时该增益更大，然而将SD 算法进行二次迭代几乎不再有额外的增益。该方案以及相应的结果不仅适用于SU－MIMO，也适用于通过多用户配对所组成的虚拟MIMO。通过对仿真结果的分析，SD 算法的适用情形初步得以明确，可以作为其工程实现的参考依据。概括地说，本文的创新点不仅包括在遵循3GPP 标准的仿真平台中实现并评估了SD 算法，也包括采用了实际(非理想)的信道估计，以及分析了不同的配置下性能增益的变化，因而从工程实现的角度弥补了现有文献的不足。在本文已完成工作的基础上，对其中所引入的SD算法的实现方案进行复杂度和收敛性等相关的理论分析，以及考虑如何针对高阶调制等情形进一步降低SD 算法的复杂度，并通过仿真评估其性能和增益的变化趋势等方面，将会作为后续的工作内容。

［1］ Sesia S，Toufik I，Baker M. LTE－The UMTS Long Term Evolution:From Theory to Practice ［M］. 2nd ed. New York:Wiley，2011.

［2］ Fincke U，Pohst M.Improved methods for calculating vectors of short length in a lattice，including a complexity analysis［J］. Mathematics of Computation，1985，44(4):363－371.

［3］ Viterbo E，Boutros J.A universal lattice code decoder for fading channel ［J］. IEEE Transactions on Information Theory，1999，45(5):1639－1642.

［4］ Agrell E，Eriksson T，Vardy A，et al.Closest point search in lattices［J］.IEEE Transactions on Information Theory，2002，48(8):2201－2214.

［5］ Guo Z，Nilsson P. Algorithm and implementation of the K－best sphere decoding for MIMO detection［J］. IEEE Journal on Selected Areas in Communications，2006，24(3):491－503.

［6］ Barbero L，Thompson J.Fixing the complexity of the sphere decoder for MIMO detection ［J］. IEEE Transactions on Wireless Communications，2008，7(6):2131－2142.

［7］ Shah M A，Mennenga B，Fettweis G. Iterative Soft－ In Soft－ Out Sphere Detection for 3GPP LTE ［C］//Proceedings of IEEE 71st Vehicular Technology Conference.Taipei:IEEE，2010:1－5.

［8］ Wang C，Tsai P.Precoder selection under K－best MIMO detection for 3GPP－ LTE/LTE－ A systems ［C］//Proceedings of 18th Asia－Pacific Conference on Communications.Jeju Island:IEEE，2012:933－938.

［9］ Liu X，He X，Ren W，et al.Evaluation of Near MLD Algorithms in MIMO SC－ FDMA System［C］//Proceedings of 2010 6th International Conference on Wireless Communications Networking and Mobile Computing. Chengdu:IEEE，2010:1－4.

［10］ Jar M，Matus E，Perez－Adeva E，et al.Two－stage detector for SC－FDMA transmission over MIMO ISI channels［C］//Proceedings of 2012 International Symposium on Wireless Communication Systems. Paris:IEEE，2012:391－395.

［11］ Moriyama M，Iwanami Y. Complexity reduction using QRD－ M or SD in MIMO Interleaved SC－ FDMA receiver with iterative detection［C］//Proceedings of 2012 International Symposium on Information Theory and its Applications.Honolulu，HI:IEEE，2012:145－149.

［12］ Studer C，Wenk M，Burg A，Bolcskei H. Soft－ Output Sphere Decoding:Performance and Implementation Aspects［C］//Proceedings of 40th Asilomar Conference on Signals，Systems and Computers. Pacific Grove，CA:IEEE，2006:2071－2076.