基于TLS 的主动全向声呐浮标目标定位与跟踪*
2015-03-18屈也频梅风华
李 涛,屈也频,梅风华
(海军装备研究院 航空装备论证研究所,上海200436)
1 引 言
声呐浮标是航空搜潜主要的潜艇定位与跟踪设备,其目标定位与跟踪算法一直是航空反潜研究的重点[1-5]。文献[6]基于HYFIX 法研究了被动全向浮标目标定位问题;文献[7]研究了多枚声呐浮标的数据融合定位问题;文献[8]基于反正切法研究了DIFAR 浮标目标定位估计方法,上述方法均通过定位方程的解算来定位目标,受测量噪声影响较为严重;文献[9]和[10]则从提高测量信息利用率的角度,分别研究了基于卡尔曼滤波的单枚、多枚被动定向浮标定位算法,缺点是需已知测量信息的误差模型,这限制了其应用;文献[11]基于泰勒展开法研究了直线运动目标的主动全向浮标定位问题,但上述文献均没有考虑浮标位置定位精度的影响。由于浮标在对目标进行监测过程中受水面的风、海流等影响,其位置在水中是随机漂移的,在航空搜潜过程中需要确定浮标在水中的位置并定期进行更新[12]。文献[13]考虑到浮标定位误差的影响,基于最小二乘法(Least Square,LS)对主动全向浮标的目标定位问题进行了研究,在浮标定位误差和目标测距误差较小的情形下取得较好的效果,但由于浮标定位存在误差,最小二乘法得出的目标位置估计实际上是有偏的,因此不适合误差较大的情形。考虑到浮标定位误差、目标测距误差的统计特性以及潜艇的运动特性,本文基于总体最小二乘法(Total LS,TLS)研究主动声呐浮标的目标定位与跟踪问题。
2 主动全向声呐浮标定位原理
主动声呐浮标一般用于在得知潜艇概略位置后的精确定位,以典型的3 枚浮标包围阵型为例,各声呐浮标的几何关系如图1所示。考虑到声呐作用距离通常要高出探测目标深度一个数量级以上,即目标垂直向的俯仰角很小,只在水平坐标内考虑目标定位。
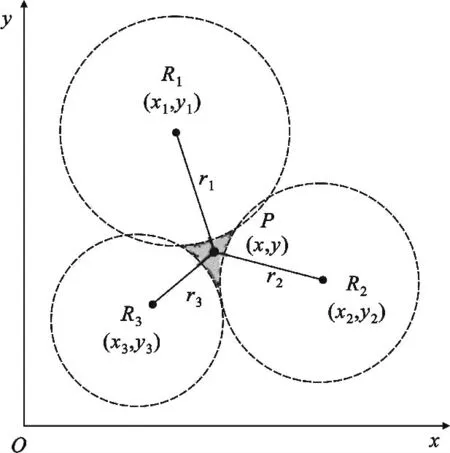
图1 主动全向声呐浮标系统定位原理Fig.1 The target positioning principle of active omni-directional sonobuoys
根据图1所示的几何关系,可得目标的定位方程为
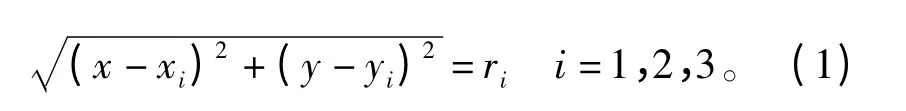
式中,ri由主动浮标根据回波延时测出,xi、yi由反潜巡逻机/直升机的声呐浮标参考系统测出。由式(1)的任意两个圆的交点可以解算出一组目标位置,由三组位置坐标的重合点最终得出实际的目标位置。实际过程中由于ri、xi、yi存在测量误差会导致3 个交点不重合,解算出的目标位置是一个区域,极端情形下甚至没有交点。为解决这一问题,由式(1)的3 个方程消去x 和y 的二次项,建立线性方程组:
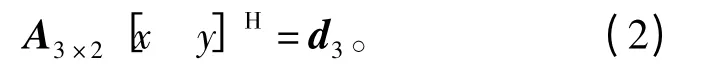
式中,H 为转置运算,且
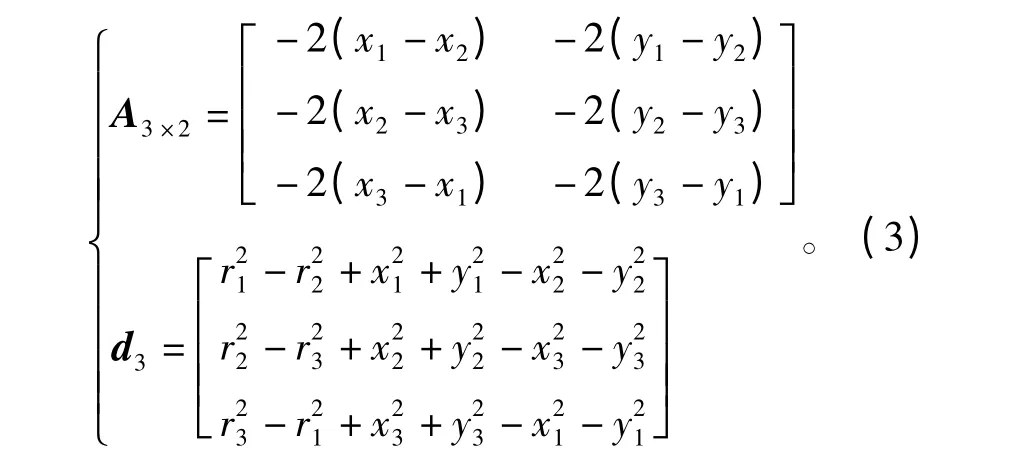
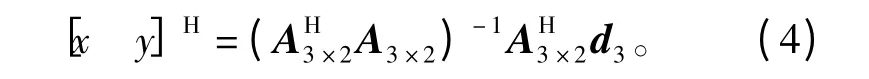
求解式(2)的最小二乘解,则观察式(3)知,当ri、xi、yi存在测量误差时,A3×2及d3均存在误差,而由于式(4)的求解过程只考虑将d3中的误差最小化,因此由式(4)解算出的目标位置实际上不是无偏估计。
3 基于总体最小二乘法的定位与跟踪算法
考虑ri、xi、yi的测量误差,在目标运动的情形下,测量误差的随机特性可以认为是固定,但不同测量对应的目标位置是变化的,即被估计量是非平稳的,考虑到潜艇运动的物理限制和规律性,相对于不同时刻的测量间隔而言其位置变化是平滑的,利用测量误差的随机性,可以采用多次测量的结果提高定位及跟踪精度。下面具体推导这一过程。
考虑潜艇的运动模型:

式中,x(k)为k 时刻目标状态向量,且
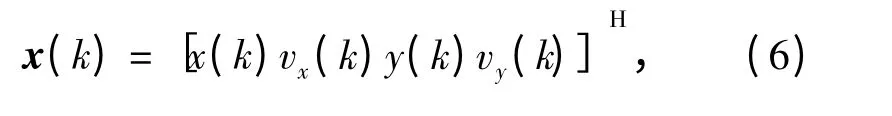
其元素分别表示潜艇的x 坐标、x 轴方向速度、y 坐标、y 轴方向速度;Φ(k)为状态转移矩阵;Γ(k)为输入控制矩阵,典型匀速直线运动状态下分别为

式中,T 为测量周期;v(k)为潜艇x 轴方向和y 轴方向的加速度状态向量,匀速直线运动状态下定义为高斯分布的白噪声向量。
对于主动全向浮标而言,能够得到的关于目标的测量为目标的距离和速度(多普勒)信息,距离信息的量测方程如式(2),速度信息的量测方程为
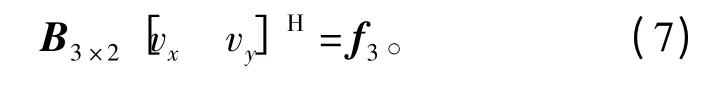
式中,
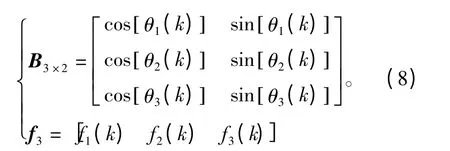
式中,fi(k)为k 时刻第i 枚浮标测得的目标径向速度,θi(k)(i=1,2,3)为k 时刻第i 浮标目标连线与x 轴的夹角,即

式(2)和式(7)可合并成量测方程:
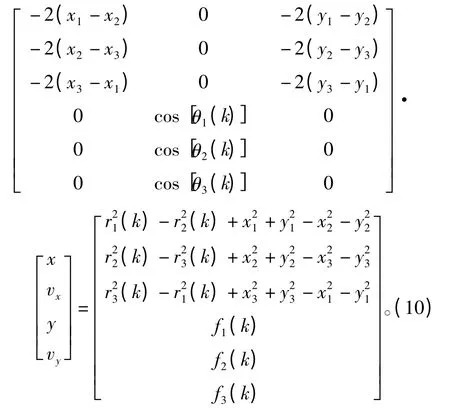
将式(10)重新定义为
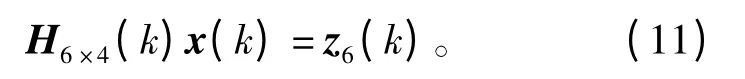
由于式(9)中存在未知量x(k)、y(k),为避免将式(11)的线性方程组非线性化,可以将式(9)中的x(k)、y(k)用式(12)中的预测值代替:

由于目标运动的随机误差以及量测误差的影响,由式(11)及(12)解算的结果均存在误差,其中式(11)如果通过最小二乘法来解算,由于H6×4(k)存在测量误差,同样会使得估计是有偏的,为此首先将式(11)改写为

式中,U(k)= [H6×4(k) z6(k)],ω(k)=[x(k) vx(k) y(k) vy(k)-1]H。通过求解式(13)的总体最小二乘解,会自然考虑U(k)中各个元素的测量误差,这一过程可以通过以下的LMS算法的递推过程来实现:
取ω0=[(k)-1],作N 次循环计算(i=0…5):
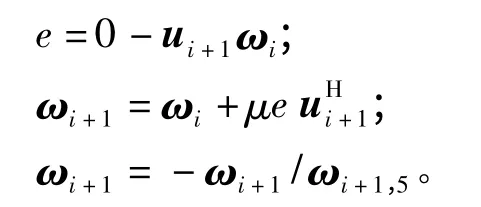
式中,ui+1(i =0…5)为U(k)的第i +1 行,ωi+1,1-4为ωi+1的第1-4 个元素,ωi+1,5为ωi+1的第5 个元素,μ 为迭代控制系数,一般取小的常值。由于每一时刻的迭代过程初值由预测值构成,为实现递推,航迹的起始点可以通过式(11)的最小二乘解给出。
4 仿真试验及结果分析
仿真试验验证算法两个方面的性能,试验1 验证算法的定位性能,试验2 验证算法的跟踪性能,均通过与最小二乘法比较来验证。
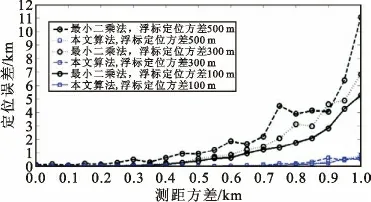
图2 定位性能仿真结果Fig.2 The simulation results of target positioning

图3 跟踪性能仿真结果(浮标定位方差为100 m)Fig.3 The simulation results of target tracking (sonobuoy position RMS=100 m)
图2中,在测距误差小于100 m 时,最小二乘法和本文算法性能相似,但当测距误差增大时,本文算法的性能明显优于最小二乘法。同时还可看出,最小二乘法对浮标定位误差非常敏感,而本文算法在不同浮标定位误差情形下均表现出类似的结果,显示其具有很好的抑制浮标定位误差影响的能力。
从图3中可以更清楚地看出,采用最小二乘法时当目标驶离浮标所围区域后,基本上已经不具备跟踪能力,采用本文算法时跟踪性能明显要优于最小二乘法,这对于潜艇的实时位置和航向解算是非常有利的。
分析上述试验结果,由本文算法的迭代过程可以看出,实际上由于k 时刻状态估计为 珓(k)预测值(k)与加权和构成,而(k)又是由珓(k-1)根据式(12)预测得来的,以此类推,珓(k)实际上是由不同时刻的测量信息非线性加权的结果,因此对测量误差起到了平滑的效果,实现了航迹的整体优化。同时,由LMS 算法随机梯度优化的性质决定了其具备跟踪非平稳估计量的性能,因此在目标存在机动的情形下,即使算法使用匀速直线运动模型进行状态预测,依然具备了较好的目标跟踪效果。
5 结束语
综上所述,本文提出一种基于TLS 算法的主动全向浮标定位与跟踪算法。算法首先对主动全向浮标的定位方程和测速方程进行变换形成线性的量测方程,然后利用潜艇测距误差和浮标定位误差的随机性,基于LMS 算法对TLS 量测方程进行递归解算,递归解算过程根据潜艇运动所受的物理限制,利用运动模型的状态预测值作为递归过程的初值,实现了航迹的整体优化。仿真结果显示算法较之最小二乘法具有更好的抑制测量误差的能力和机动目标跟踪能力,对于主动全向声呐浮标的目标定位具有一定应用价值。
[1] Coraluppi S. Multistatic sonar localization[J]. IEEE Journal of Oceanic Engineering,2006,31(4):964-974.
[2] Sergey S. Localization in airborne multistatic sonars[J].IEEE Journal of Oceanic Engineering,2008,33(3):278-288.
[3] 胡柱喜,孙明太,苏维国,等. 被动定向浮标LOFIX 定位精度分析[J]. 电光与控制,2009,16(12):26-29.HU Zhuxi,SUN Mingtai,SU Weiguo,et al. Simulation Analysis of LOFIX Fixing Accuracy for Passive Omnidirectional Sonobuoy[J]. Electronics Optics & Control,2009,16(12):26-29.(in Chinese)
[4] 王隽,王英民,陶林伟. 浮标定位算法的仿真研究[J].声学技术,2009,28(6):95-98.WANG Jun,WANG Yingmin,TAO Linwei. The simulation and research on the sonobuoy location algorithm[J].Technical Acoustics,2009,28(6):95-98.(in Chinese)
[5] 杨蕾. 被动型声纳浮标定位技术研究[D]. 哈尔滨:哈尔滨工程大学,2009.YANG Lei. Study of Passive Sonar Buoys Location Technology[D]. Haerbin:Haerbin Engineer University,2009,.(in Chinese)
[6] 孙辉,孙明太,刘京莲. 被动全向浮标HYFIX 定位精度仿真分析[J]. 电光与控制,2010,17(1):85-88.SUN Hui,SUN Mingtai,LIU Jinglian. Simulation Analysis on HYFIX Locating Accuracy of Passive Omnidirectional Sonobuoy[J]. Electronics Optics & Control,2010,17(1):85-88.(in Chinese)
[7] 魏继国,屈也频. 航空声纳浮标定位的数据融合方法研究[J]. 航空电子技术,2008,39(2):34-38.WEI Jiguo,QU Yeping. Data Fusion Analysis Applied to Airborne Sonobuoy Positioning[J]. AVIONICS TECHNOLOGY,2008,39(2):34-38.(in Chinese)
[8] 孔银垒,王英民. DIFAR 浮标反正切目标方位估计方法[J]. 声学技术,2010,29(4):370-373.KONG Yinlei,WANG Yingmin. Research on arctangent bearing estimation of DIFAR sonobuoy[J]. Technical Acoustics,2010,29(4):370-373.(in Chinese)
[9] 陶林伟,王英民. 一种新的单枚被动定向浮标目标定位方法[J]. 兵工学报,2011,32(3):365-369.TAO Linwei,WANG Yingmin. A Target Location Algorithm Based on Single Direction Finding and Ranging Sonobuoy[J]Acta Armamentarii,2011,32(3):365-369.(in Chinese)
[10] 陶林伟,王英民. 基于扩展卡尔曼滤波的DIFAR 浮标阵定位算法及分析[J]. 西北工业大学学报,2011,29(5):738-744.TAO Linwe,WANG Yingmin. DIFAR(Direction Finding and Ranging)Sonobuoy Array Tracking Algorithm Based on Extended Kalman Filter(EKF)[J]. Journal of Northwestern Polytechnical University,2011,29(5):738-744.(in Chinese)
[11] 董志荣. 主动声呐浮标目标运动分析数学模型[J].电光与控制,2007,14(1):5-9.DONG Zhirong. Mathematical models for target moving analysis through active son buoy[J]. Electronics Optics& Control,2007,14(1):5-9.(in Chinese)
[12] 张欣,杨日杰,汤燕. 基于扩展卡尔曼滤波的浮标定位方法[J]. 火力与指挥控制,2005,30(4):59-62.ZHANG Xin,YANG Rijie,TANG Yan.Research of Buov Location Calculation Method based on Extended Kalman Filter[J]. Fire Control and Command Control,2005,30(4):59-62.(in Chinese)
[13] 杨日杰,周旭,张林琳. 主动全向声纳浮标跟踪潜艇优化布放方法[J]. 系统工程与电子技术,2011,33(10):2249-2253.YANG Rijie,ZHOU Xu,ZHANG Linlin. Optimal deployment of active omni- directional sonobuoys in underwater target tracking[J]. Systems Engineering and Electronics,2011,33(10):2249-2253.(in Chinese)
