非对称基坑开挖监测位移下数值对比分析

2015-03-18刘云波朱有奇

河北工程大学学报(自然科学版) 2015年2期

刘云波，朱有奇，杨德，赵建

(1.河海大学岩土工程科学研究所，江苏南京210098;2.上海瀚联建筑设计咨询公司河南分公司，河南郑州450000)

目前，实际工程中有很多问题由于边界条件较为复杂，很难通过计算求出其解析解，只有当边界条件比较简单、规则，且方程的性质比较特殊时，才能进行解析解的计算。随着有限单元法和计算机技术的发展，使有限元分析成为解决复杂工程问题的一个有效途径［1］。朱有奇、卢国胜等［2－6］在分析主动土压力、被动土压力和静止土压力与位移关系的基础上，根据朗肯土压力理论，提出了考虑位移的土压力计算方法;徐日庆、龚慈［7－9］等针对绕墙底向外转动的刚性挡土墙，提出了一种简单可行的土压力计算方法，采用改进的库仑主动土压力公式计算各转角下的土压力分布，用于绕墙底向外转动位移模式下挡土墙的设计及验算;徐日庆［9］等研究了考虑平动位移效应的非极限状态土压力计算理论，通过比较，发现理论公式计算结果与模型试验结果较吻合。

本文主要以现场监测数据为依据，根据ABAQUS数值模拟，对现场监测数据位移与数值模拟位移进行比较分析。

1 工程概况

本工程监测区域为南京青奥轴线地下工程B2－J1区基坑工程，该区为盆式基坑，开挖8 m深度以下包含数个内嵌基坑，具体为梅子洲主线隧道YK10+312－－YK10+525段基坑、J匝道JK0+206.5－－JK+0319.354 段基坑、M 匝道MK0+228.142－－ MK0+346.043 段基坑、L 匝道 LK0+228.632－－LK0+381.551 段基坑、I匝道 IK0+082.139—IK0+117.646 段基坑与青奥中心、国际风情街的地下连通道基坑［2］。本文重点对B2－J1区主隧道基坑的开挖情况进行监测分析，并与ABAQUS数值模拟分析对比。

2 ABAQUS基坑开挖的有限元模拟

有限元法不仅可以模拟基坑开挖的全过程，还可以计算支护结构弯矩、支撑轴力以及土体的应力和位移。根据实际情况在数值分析中做出以下假设［1］:

(1)不考虑土体的流变影响。

(2)不考虑温度对支撑轴力的影响。

(3)土体性质为各向均质同性，土体本构模型采用Mohr－Coulomb理想弹塑性模型。

(4)不考虑基坑降水开挖对土体性质的影响。

2.1 模型建立

2.1.1 计算区域及边界条件

我们所要计算的区域一般是开挖时对土体有影响的区域，理想情况下，当土体不发生位移时，土体的受力也就不会改变，也就是说计算区域要取到土体不发生变形的边界处。但是由于计算条件有限，不可能完全实现这种情况，因此为重点分析支护结构变形和作用在支护结构上的作用力，模型侧边界取大于基坑开挖深度的2倍，模型底面边界取大于基坑开挖深度的3倍。模型上施加的边界约束条件为:模型两侧边界的水平位移被限制，底部边界的水平和竖向位移都被限制［3］。

2.1.2 单元划分

在有限元模型中，土层采用 4节点的 CPE4实体单元模拟，地下连续墙采用梁单元B21进行模拟，划分网格。

2.1.3 参数选取

根据地质勘查报告揭示的土层情况，计算中将土层简化，划分为5层，综合考虑地质资料后，各层土和地下连续墙的计算参数取值见表1［2］。

2.1.4 初始地应力的平衡

在岩土工程中，初始地应力的实际存在使得土体开挖导致开挖土体应力关系的改变，因此基坑周围的应力场也随之发生改变。随着开挖的施工进程的进行，基坑的性状也不断改变。ABAQUS提供了实现初始地应力平衡的功能，利用单元的“生死功能”和分步分析计算的方式来模拟开挖过程，使得土体开挖过程和应力情况与实际情况基本符合［4］。

2.1.5 开挖过程模拟

根据基坑开挖和支护结构的施工工序，模拟分析中主要考虑四个施工阶段。针对分步开挖的情况，我们可以利用 ABAQUS中的“生死单元”功能来实现分步开挖土体的模拟，而支撑的架设可以通过开挖后控制土体边界条件来实现，基本步骤为:

步骤1:施加土体重力，建立初始地应力场。步骤2:开挖第一层土体，开挖深度为8.5 m，通过*Model change，remove实现。

步骤3:开挖第二层土体，开挖深度为5 m，通过*Model change，remove实现。

表1 各层土和地下连续墙的计算参数取值Tab.1 Parameter values of layers of soil and underground continuous wall

步骤4:开挖第三层土体，开挖深度为4 m，通过*Model change，remove实现。

步骤5:开挖第四层土体，开挖深度为4 m，通过*Model change，remove实现。

2.2 数值模拟的结果分析

2.2.1 实测水平位移与模拟结果的分析

从图1—图3中可以看出:墙体水平位移与实际监测变化趋势基本符合，首先是悬臂开挖的墙顶向外发生三角形分布的位移［5］，然后随着开挖深度的增加和支撑的架设，墙体开始发生转动，支撑以上墙体向坑外移动，支撑以下土体发生鼓形变形［5］;最大位移点位置逐渐地下降，且最大位移也逐渐增大。当开挖至基坑底部时，墙体因为土体卸荷的原因，导致基坑底部以下土体对墙体低端的约束减弱，从而使得墙低端出现了向坑内的位移。

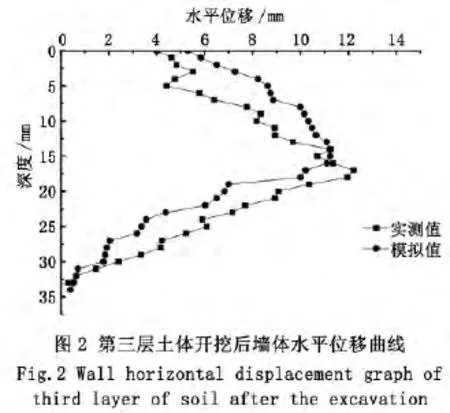
2.2.2 土压力数值结果与计算结果对比分析

当h1=8、4 m时，分别取H=20、30 m时土压力分布图如图4、图5。

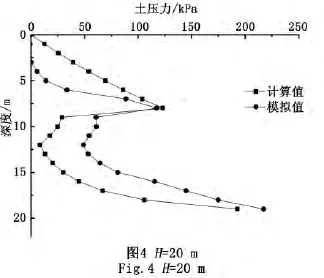
从图中可以看出:在开挖面附近的土压力，随着墙体高度的增加而增大［7］。在支撑以上部分，模拟值要小于计算值;而在开挖面以下部分，则模拟值大于计算值［8］。反映出了模拟值并未达到极限状态，而计算值是按照极限状态来计算的。悬臂段土体还要受到墙体的被动土压力的影响而增加，二级开挖段墙体还要继续向前移动，土压力继续减小［9］。