《乐学轨范》律数考

桑 坤

《乐学轨范》律数考

桑 坤

《乐学轨范》继承了朱熹、蔡元定的律学成果，使用“九分寸法”精确计算了十二律的长度，并将大吕、夹钟、仲吕三律的倍半之数并列在同一组数据中，统合了蕤宾后下生和蕤宾后重上生两种三分损益生律顺序所产生的不同律学结果。

乐学轨范；律吕新书；琴律说；九分寸法；三分损益法

《乐学轨范》（成书于1493年）卷一《音调律吕诸图说》中，对十二律管长度予以计算，原文如下：

黄钟长九寸’围九分’以下十一律围并同’三分损一下生林钟；

大吕长四寸一分八厘三毫’三分益一上生夷则’倍数长八寸三分七厘六毫；

太簇长八寸’三分损一下生南吕；

夹钟长三寸六分六厘三毫六丝’三分益一上生无射’倍数长七寸四分三厘七毫三丝；

姑洗长七寸一分’三分损一下生应钟；

仲吕长三寸二分八厘六毫二丝三忽’倍数长六寸五分八厘三毫四丝六忽’以七百二十九乗’三分益一口生变黄钟；

蕤宾长六寸二分八厘’三分损一下生大吕；

林钟长六寸’三分益一上生太簇；

夷则长五寸五分五厘一毫’三分损一下生夹钟；

南吕长五寸三分’三分益一上生姑洗；

无射长四寸八分八厘四毫八丝’三分损一下生仲吕；

应钟长四寸六分六厘’三分益一上生蕤宾。［1］725-726

上列数据看起来并非严格的三分损益法，从应钟一律起，数据明显与损益相生之所得有较大出入。后几律可以计算到毫、丝、忽及忽以下的细微数据，但南吕、姑洗两律仅计算到“分”，这里为什么不需要更精确？大吕、夹钟、仲吕三律各有“半下生长”、“全倍数重上生长”①见《乐学轨范·卷一·十二律围长图说》律管图中文字标识。（即其半、倍管长）两个数据，但从数字上看又不是简单的倍半关系，这样的数据是如何产生的呢？不过，这组奇怪的数据对我却并不陌生。数年前，在研读朱熹《琴律说》时就接触过这组数据，在蔡元定《律吕新书》中，也有相同数据。

一、《乐学轨范》十二律数的来源

朱熹（1130-1200）在其《琴律说》一文（至迟成书于宋宁宗年间，1195年-1200年）中言明，他使用“太史公九分寸法”（即九进制）对十二律数进行计算。其原文为：

十二律数曰：黄钟九寸’为宫。琴长九尺而折其半’故为四尺五寸’而下生林钟。林钟六寸’为徵。为第九徽。徽内三尺’徽外一尺五寸。上生太簇。太簇八寸’为商。为第十三徽。徽内四尺’徽外五寸。下生南吕。南吕五寸三分’为羽。为第八徽。徽内二尺七寸’徽外一尺八寸。上生姑洗。姑洗七寸一分’为角。为第十一徽。徽内三尺六寸’徽外九寸。下生应钟。应钟四寸六分六厘。位在八徽内二寸七分。内二尺四寸’外二尺一寸。上生蕤宾。蕤宾六寸二分八厘。位在十徽、九徽之间。内三尺一寸五分’外一尺三寸五分。上生大吕。大吕八寸三分七厘六毫。在龙龈内二寸半。内四尺二寸半’外二寸半。下生夷则。夷则五寸五分五厘一毫。在九徽、八徽之间。内二尺八寸半’外一尺六寸半。上生夹钟。夹钟七寸四分三厘七毫三丝。为第十二徽。徽内三尺八寸’徽外七寸。下生无射。无射四寸八分八厘四毫八丝。在八徽内。徽内二尺五寸’徽外二尺。上生中吕。中吕六寸五分八厘三毫四丝六忽。为第十徽’亦为角。徽内三尺四寸’徽外一尺一寸。复生变黄钟’八寸七分八厘有奇。今少宫以下即其半声’为四寸三分八厘有奇也。以上十二律’并用太史公九分寸法约定。《周礼》郑注以从简便’凡律’寸皆九分’分皆九厘’厘皆九丝’丝皆九忽。琴尺皆十寸’寸皆十分’分皆十厘’厘以下不收。［2］

朱子对十二律的计算方法是损益相生，蕤宾后重上生，使十二律高保持在一个八度之内。与《乐学轨范》中的律数作一对比，二者几乎完全相同，不同的是，《琴律说》由于“蕤宾后重上生”的步骤，使得大吕、夹钟、仲吕三律处于黄钟和清黄钟之间，而《乐学轨范》使用损益交替相生，大吕、夹钟、仲吕三律则必然高于清黄钟，所以《乐学轨范》作者补充了此三律的倍数。见下表：

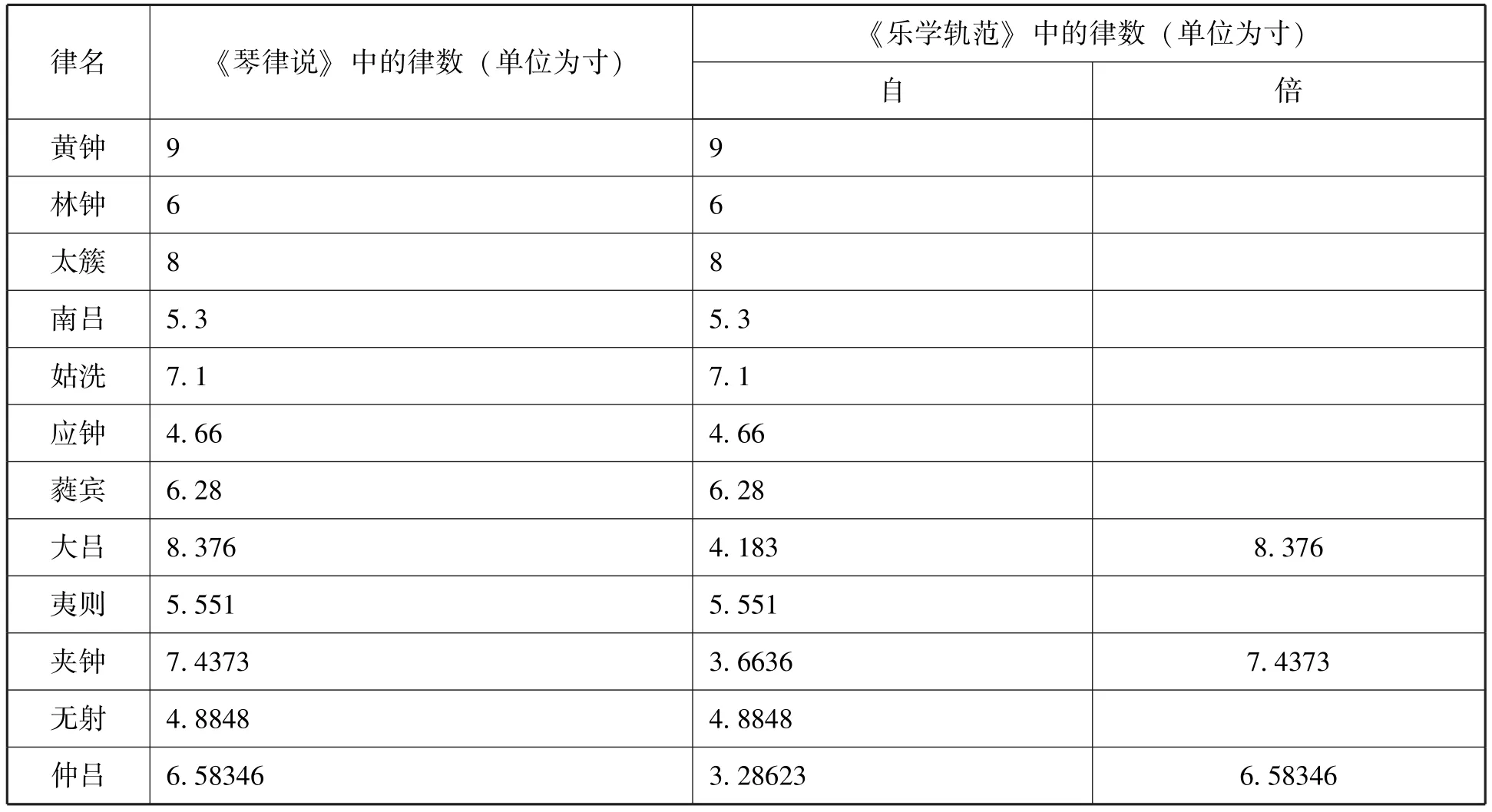
表一

朱熹在《琴律说》中解释使用九分寸法运算的原因为“以上十二律，并用太史公九分寸法约定。《周礼》郑注以从简便，凡律，寸皆九分，分皆九厘，厘皆九丝，丝皆九忽。”归因于从古，朱熹认为这样的运算有一定的理论渊源，遵循了从《史记》以来研究三分损益生律的方法，实践了《周礼》中郑玄对律长计算中的单位计量方式。

在蔡元定《律吕新书》（约成书于1186年）卷一的《十二律之实第四》中，蔡元定对十二律管的容积及长度有这样的计算结果：

子’黄钟’十七万七千一百四十七’全九寸’半无；

丑’林钟’十一万八千口口九十八’全六寸’半二十①此为文渊阁《四库全书·经部·乐类·律吕新书卷一·十二律之实第四》原文，“二十”疑为“三寸”。’不用；

寅’太簇’十五万七千四百六十四’全八寸’半四寸；

卯’南吕’十口万四千九百七十六’全五寸三分’半二寸六分不用；

辰’姑洗’十三万九千九百六十八’全七寸一份’半三寸五分；

巳’应钟’九万三千九百一十二’全四寸六分六厘’半二寸三分三厘不用；

午’蕤宾’十二万四千四百一十六’全六寸二分八厘’半三寸一分四厘；

未’大吕’十六万五千八百八十八’全八寸三分七厘六毫’半四寸一分八厘二毫；

申’夷则’十一万口口五百九十二’全五寸五分五厘一毫’半二寸七分二厘五毫；

酉’夹钟’十四万七千四百五十六’全七寸四分三厘七毫三丝’半三寸六分六厘三毫六丝；

戌’无射’九万八千三百口口四’全四寸八分八厘四毫八丝’半二寸四分四厘二毫四丝；

亥’仲吕’十三万一千口口七十二’全六寸五分八厘三毫四丝六忽’余二算’半三寸二分八厘六毫二丝二忽。［3］

他将十二律按照相生顺序进行排列，每一律都列出了全、半之数，有些数据标注不用。《乐学轨范》中出现的数据均可在这里找到。对比如下：

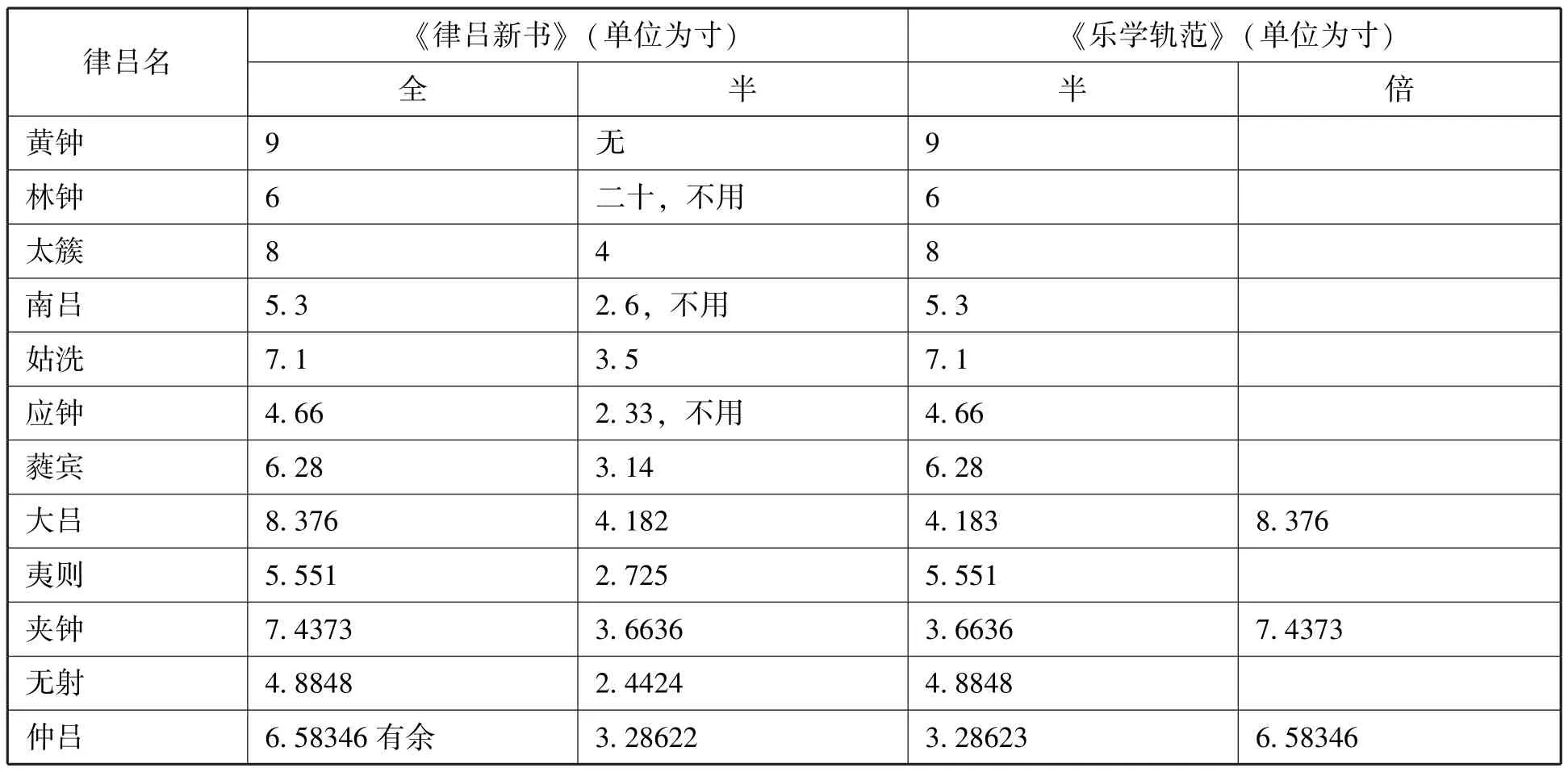
表二

由上表可见，《乐学轨范》中出现的十二律数据与《律吕新书》亦是几乎完全一致，只是在大吕、仲吕两律上在小数点后第五位出现微小差异（表二中使用斜体标出）。此两律自倍关系明显，这个差异疑因《律吕新书》传抄讹误造成。

在《律学新书》中，蔡元定与朱子一样，使用“九分寸法”计算律长，除了循古，他还对九进制所算得数据总结出一个工艺范畴的意义：

案十二律之实约以寸法’则黄钟、太簇得全寸；全寸约以分法’则南吕、姑洗得全分；约以厘法则应钟、蕤宾得全厘；约以毫法则大吕、夷则得全毫；约以丝法则夹钟、无射得全丝。至仲吕之实十三万一千七十二’以三分之不尽’二算其数不行’此律之所以止于十二也。［3］

观察这三组“九分寸法”数据，确实如蔡元定所述，从南吕起，每两律在小数点后多一位。一寸是九分，一分是九厘，在单位“寸”内整除不尽，便约在“分”内除，再不尽就往“厘”、“毫”、“丝”、“忽”这些单位内进行计算。现在我们来还原一下蔡元定的计算过程。

以“太簇长八寸，三分损一下生南吕”为例，已知太簇律长8寸，求三分损一后的南吕律长，即“九分寸法”下计算8（寸）×。过程如下：

第一步，三其法：

2寸×9＝18（分），18÷3＝6（分）

八寸三分之即8÷3＝2.6（寸）

第二步，倍其实：

2.6寸×2＝2×2＋0.6×2＝4寸＋12分（9＋3）＝4寸＋1寸＋3分＝5.3（寸）

使用上述方式计算，体现了古人的智慧。三分损益法以3为除数，“九分寸法”下，被除数除以3，可通过增加小数点后位数得到相对简单的有理数，方便计算。如此计算所得，远比十进制下因不断三分以致出现的复杂结果要简明许多。

通过爬梳文献可见，《乐学轨范》继承了朱熹、蔡元定的律学思维。《乐学轨范》对蔡元定的乐律学思想是十分推崇的，其序言中明确讲到“惟蔡元定之书深得律吕之源。”《琴律说》与《律吕新书》中对十二律的计算均是以损益相生为顺序，而《乐学轨范》则是按照律管长度、音高清浊次第排序，并将数据列在管律图后，体现了其力图以“道”制“器”的意图。如此精确的真数领域内三分损益的得数，目的是计算律管长度，但忽视了实践中管律应出现的管口校正的问题。虽然其数据精确到九进制下小数点后五位，在同径律管的实践中所得音高未必能达到如此精准。

二、关于《乐学轨范》中的十二律数

由上文可见，“九分寸法”是解读《琴律说》《律吕新书》《乐学轨范》中律数的关键。“九分寸法”与西方现代数学中的九进制之间，虽然计算过程与出发点并不相同，但其计算结果是一致的。为使《乐学轨范》的律数更直观地展示其三分损益计算的准确性，笔者将《乐学轨范》中的数据转换为易于理解的十进制（见表三左起第三列）。进制转换是现代数学的基础内容，它的计算方法是数码乘以相应权之和。数码是表示数的符号，权指每一位所具有的值。

数制九进制十进制数码0-8 0-9权90，91，92……100，101，102……特点逢九进一逢十进一

例如南吕律数5.3，换算为十进制：

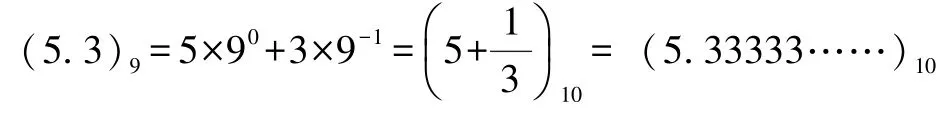
再如应钟律数4.66，换算为十进制：

如此类推，将九进制的十二律长全部换算为十进制数据，详见表三左起第三列。

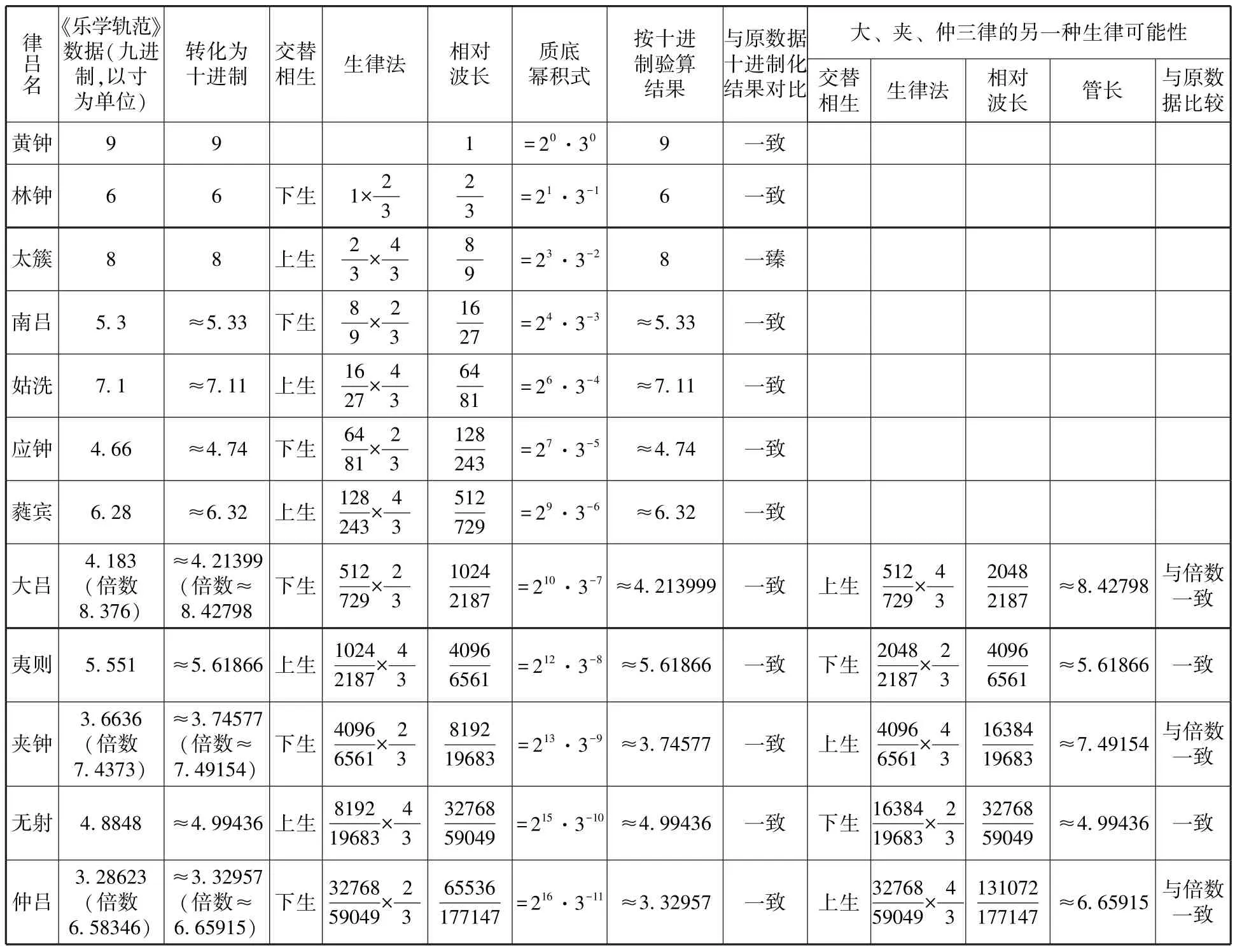
表三

上表中左起第八列是在十进制中从九寸黄钟起，以三分损益法重新演算的十二律数，很明显它与第三列的数据完全一致，《乐学轨范》的这组数据非常精确。

表三中另以分数形式列出生律法，由此计算出相对波长，并转写为质底幂积式，十二律的相生方法及生律顺序一目了然。由此可见，这组建立在九进制基础上的数据严格遵照三分损益法计算，所得结果十分精确，精确度可在九进制下达到小数点后五位，换算成十进制可达小数点后十位开外。其相生方式是损益相间，但是其中大吕、夹钟、仲吕三律各出现倍、半两组数据，经过验算可知，如果保持蕤宾后下生，可得到此三律半数，其相生次序与《史记·生钟分》相同，在音域上就会形成超出八度的排列。假设蕤宾后重上生，那么将得出此三律的倍数，可将十二律排列在一个八度内，这又暗合《吕氏春秋》的相生结果。借用五线谱记谱，以相生顺序可排列为：

综上所述，《乐学轨范》以九进制为基础，精确计算了十二律的长度，并将大吕、夹钟、仲吕三律的倍半之数并列在同一组数据中，统合了蕤宾后下生和蕤宾后重上生两种方式所产生的不同的乐律学结果。可惜的是在《乐学轨范》一书中并未明确指出其律数使用九分寸法运算。

三、一个小问题

在《乐学轨范》十二律数中，对仲吕一律的描述是这样的：

仲吕长三寸二分八厘六毫二丝三忽’倍数长六寸五分八厘三毫四丝六忽以七百二十九乗’三分益一口口生变黄钟。［1］726

其中的“以七百二十九乗”显得突兀，令人不解。是余数吗？还是有其他含义？

原来这是蔡元定在计算变律时的一个手段。《律吕新书》在解释六变律时提到设七百二十九这一数的由来：

变律者其声近正’而少高于正律也。然仲吕之实一十三万一千口口七十二以三分之’不尽’二算既不可行’当有以通之律。当变者有六’故置一而六’三之得七百二十九’以七百二十九因仲吕之实十三万一千口口七十二’为九千五百五十五万一千四百八十八’三分益一’再生黄钟、林钟、太簇、南吕、姑洗、应钟六律’又以七百二十九归之’以从十二律之数。记其余分’以为忽秒’然后洪纖高下’不相夺伦。至应钟之实六千七百一十口万八千八百六十四以三分之又不尽’一算数又不可行’此变律之所以止于六也。［4］

原来七百二十九这个数字的确立是由于“仲吕之实”无法继续三分损益生出变黄钟，为了方便计算，借用数36＝729，来完成六变律的计算。因此，“以七百二十九乗”，就是指剩下的计算需要使用仲吕实数乘以729，获取一个更大的数来继续。仲吕一律后紧跟这一句，显示了《乐学轨范》的作者对蔡元定六变律思维的洞悉。不过在原文献中，《十二律围图说》一节一直只在管长这一维度中讨论十二律，并未涉及变律和实积的问题，突然出现“实积”这个范畴的数据，显得有些突兀。

小 结

《乐学轨范》一书中对十二律的计算是精确的，它使用了九分寸法进行运算，有效避免了十进制下小数点后面位数过多的问题。这种做法来源于南宋朱熹和蔡元定的理论积淀，但《乐学轨范》也并未一味传抄，而是择取与《史记·生钟分》相同的损益相间、蕤宾后下生的生律方式，获得十二律的本数，又将大吕、夹钟、仲吕三律的倍数一并列入，暗合《吕氏春秋》以来蕤宾后重上生的生律方式，使十二律可以在一个八度内得到统合。这种综合两种三分损益生律顺序产生的集合，最大程度上总结了当时的乐律学成果，具有较高的学术价值。

(责任编辑：黄向苗)

［1］成俔.乐学轨范：卷一·十二律围长图说［M］.影印本.

［2］朱熹.琴律说［M］／／御纂朱子全书：卷四十一·乐.刻本.北京：武英殿，1714.

［3］蔡元定.律吕新书：卷一·十二律之实第四［M］／／四库全书：经部·乐类.上海：上海古籍出版社，2003.

［4］蔡元定.律吕新书：卷一·变律第五［M］／／四库全书：经部·乐类.上海：上海古籍出版社，2003.

Text Research on Musical Temperament in Standard of Music Discipline

SANG Kun

The book Standard of Music Discipline inherited Zhu Xi and Cai Yuanding's achievements on temperament，and applied novenaryon to accurately calculate the length of the twelve temperament.It recorded the data of both the half and whole length of the three temperaments in the list，namely dalv，jiazhong and zhonglv，and integrated the different results of two sanfen sunyi methods.

Standard of Music Discipline；the New Book of Temperament；On Temperament of guqin；novenary；Sanfen Sunyi method

J612.1

A

2015-10-05

桑坤（1986— ），女，山东泰安人，中国艺术研究院在读博士研究生，主要从事中国音乐史与音乐形态学研究。（北京100027）