二阶退化双曲型方程的第二Darboux问题及其推广和应用

赵晓辉， 闻国椿，杨广武

(1.河北科技大学 理学院，河北 石家庄 050018； 2.河北工程技术学院 经济管理学院，河北 石家庄 050091;3.北京大学 数学科学院 100871)

二阶退化双曲型方程的第二Darboux问题及其推广和应用

赵晓辉1，2， 闻国椿3，杨广武1

(1.河北科技大学 理学院，河北 石家庄 050018； 2.河北工程技术学院 经济管理学院，河北 石家庄 050091;3.北京大学 数学科学院 100871)

本文主要给出一般区域上的Darboux第二问题与一般斜微商问题解的表示式，进而使用复分析的方法证明了这些问题解的存在性与唯一性。本文中得到的结果，可用来解决一般区域上的广义chaplygin方程的Tricomi问题。

退化双曲型方程；广义Darboux问题；解的存在唯一性

1 二阶退化双曲型方程的Darboux第一问题简介

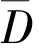
uxx-uyy+aux+buy+cu+d=0，(a,b,c,d均为x,y的已知函数)

的Darboux第一和第二问题，且所加条件较强。而对于在较弱条件下求解退化双曲型方程的Darboux问题。文献[5]属于这方面的新成果，但未及讨论第二Darboux问题。本文主要来讨论二阶退化双曲型方程的第二Darboux问题和斜微商问题，所得到结果，可用来解决一般区域上广义Chaplygin方程的Tricomi问题，Tricomi问题对空气动力学中的有关问题有着重要的应用。

我们首先考虑二阶线性退化双曲型方程

K(y)uxx+uyy+aux+buy+cu+d=0,(x,y)∈D,

(1)

其中D是由X轴上的线段L0=(0,2)与下半平面中两条特征线

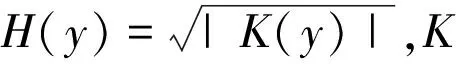
假定方程(1)的系数满足条件C：

(2)

方程(1)的Darboux第一问题可表述为：

u(z)=φ(z),z∈L1,u(x)=ψ(x),x∈L0,

(3)

其中φ(z),ψ(x)满足条件

(4)

这里α(0<α<1),k2都是非负常数.

下面引入方程(1)更一般的边值问题：

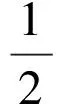
(5)

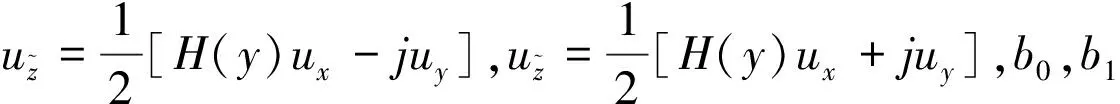
(6)

其中α(0<α<1),k0,k2都是非负常数.不难看出，前述问题D是问题P的一种特殊情形.

本文中要用到文献[5]中已证明的下述定理：

定理1 如方程(1)满足条件C，则(1)的Darboux型问题P是唯一地可解的.

2 二阶退化双曲型方程的广义Darboux第二问题

(7)

考虑在区域D′上的方程(1)带有如下边界条件的斜微商边值问题(问题P′)：

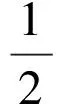
(8)

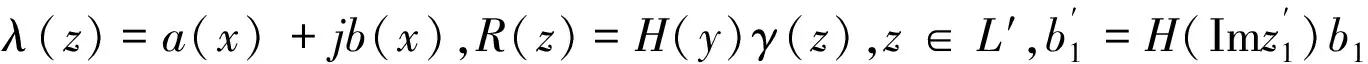
Cα[λ(z),L′]≤k0,Cα[γ(z),L′]≤k2,

(9)

这里α(0<α<1),k0,k2都是非负常数.

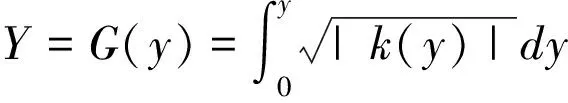
(10)

μ=2σ(ν)-ν=2σ(x+γ1(x))-x-γ1(x),0≤x≤l我们作如下变换

(11)

其中ν,μ都是实变量.以上变换的逆变换为

(12)

不难看出，变换(11)把区域D′映射为区域D，又变换(11)及其逆变换(12)可写成

(13)

与

(14)

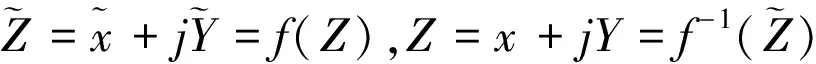
ξμ=Aξ+Bη+E,ην=Cξ+Dη+F,z∈D′

(15)

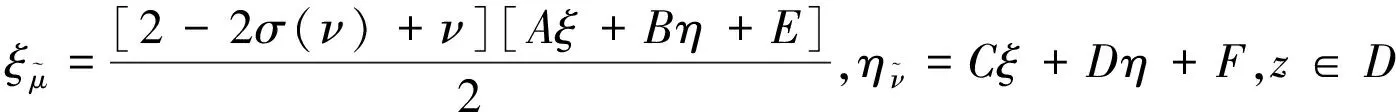
(16)

而通过变换(13)，边界条件(8)可转化为

(17)

定理2 设方程(1)在D′上满足条件C，则方程(1)的问题P′存在唯一解u(z).

(2)其次，考虑区域D″是以L0∪L″1∪L″2为边界的单连通区域，其中L″1,L″2的表示式为

L″1={γ1(x)+y=0,0≤x≤l},L″2={γ2(x)+y=0,l≤x≤2}

(18)

(19)

的Riemann-Hilbert问题(问题A′)，其中z″1=l-jγ1(l)=l-jγ2(l),又λ(z),γ(z)满足条件

Cα[λ(z),Γ]≤k0,Cα[γ(z),Γ]≤k2,Cα[λ(z),L″1]≤k0

(20)

ν=2τ(μ)-μ=2τ(x-γ2(x))-x+γ2(x),l≤x≤2

(21)

作变换

(22)

其中μ,ν都是实变量.上述变换的逆变换为

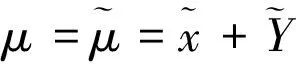
(23)

于是

(24)

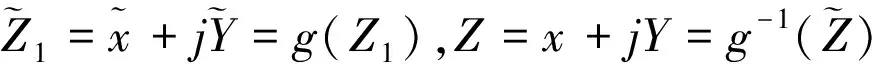
(25)

又方程组(15)转化为

(26)

而通过变换(24)，在L0∪L″1∪L″2上的边界条件转化为

(27)

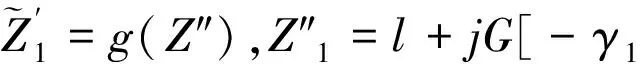
定理3 如果方程(1)在带有边界L0∪L″1∪L″2的区域D″上满足条件C，且在L″上满足边界条件(19)，则问题P″存在唯一解u(z).

[1]BitsadzeA.V,Someclassesofpartialdifferentialequations[M].NewYork:GordonandBreach,1988.

[2]BitsadzeA.V，NakhushevAN.Theoryofdegeneratinghyperbolicequations[J].Dokl.Akad.NaukSSSR， 204(1972)：1289-1291(Russian).

[3]ProtterM.H.TheCauchyproblemforahyperbolicsecondorderequationwithdataontheparabolicline[J].Can.J.Math.6(1954): 542-553.

[4]WenGuochun.Linearandquasilinearcomplexequationsofhyperbolicandmixedtype[M].London:Taylor&Francis,2002.

[5]WenGuochun.Darbouxtypeproblemfordegeneratehyperbolicequationsofsecondorder[J].数学进展，2007,36(4):467-475.

[6] 闻国椿、杨广武、黄沙,等.广义解析函数及其拓广[M].石家庄：河北教育出版社，1989.

[7] 闻国椿.线性与非线性椭圆型复方程[M].上海：上海科学技术出版社，1986.

Generalized darboux’s second problem for degenerate hyperbolic equations

ZHAO Xiao-hui1，2， WEN Guo-chun3，YANG Gang-wu1

(1.SchoolofSciences,HebeiUniversityofScienceandTechnology,ShijiazhangHebei050018,China； 2.SchoolofEconomicsandManagement,HebeiPolytechnicInstitute,ShijiazhangHebei050091,China; 3.SchoolofMathematicalSciences,PekingUniversity,Beijing100871,China)

The present paper deals with some boundary value problems for the degenerate hyperbolic equations of second order,mainly the representation of solutions for Darboux’s second problem and general oblique derivative problem in general domains is given,and the existence and uniqueness of solutions for the problems are proved.The results in this paper can be used to solve Tricomi problem of generalized Chaplygin equations in general domains.

Degenerate hyperbolic equations； Generalized Darboux’s second problem； Existence and uniqueness of solutions

2015-06-21

国家自然科学基金资助(10471149)；河北省教委基金资助(2350044)

赵晓辉(1982-)，女，河北顺平人，硕士研究生，讲师，主要从事偏微分方程的函数论方法研究及模糊数学.

1001-9383(2015)03-0001-06

O175

A