带未知观测输入和观测丢失多传感器随机不确定系统的集中式融合滤波
2015-03-17逄崇雁孙书利
逄崇雁,孙书利
(黑龙江大学 电子工程学院,哈尔滨 150080)
带未知观测输入和观测丢失多传感器随机不确定系统的集中式融合滤波
逄崇雁,孙书利*
(黑龙江大学 电子工程学院,哈尔滨 150080)
对带未知观测输入和观测丢失的多传感器随机不确定系统设计了集中式融合滤波器。通过乘性噪声描述的随机不确定性存在于系统的状态和观测矩阵中。在没有观测干扰任何先验信息的情况下,应用线性无偏最小方差准则,设计了不依赖于未知观测输入的具有Kalman形式的集中式融合滤波器。仿真验证了算法的有效性。
未知输入;观测丢失;乘性噪声;集中式融合滤波;线性无偏最小方差
0 引 言
由于未知输入在系统故障检测与分离等方面有重要应用,带未知输入系统的状态评估问题得到了众多学者的关注。以往文献对带未知输入系统的滤波问题的研究已有较多报道。在没有未知输入先验信息的情况下,文献[1]在线性最小方差意义下给出了一种三步递推Kalman滤波器。文献[2]利用奇异值分解设计了一种状态滤波器。文献[3]针对非线性系统,通过设计降维观测器和高阶滑膜观测器给出状态和未知输入同时估计方法。除了未知输入的影响,在网络系统中,由于网络宽带限制及外界干扰影响,观测数据不可避免会出现观测丢失及乘性噪声干扰现象。对于带观测丢失的系统,文献[4]利用满足Bernoulli分布的随机变量表示观测丢失,给出了线性最小方差滤波器。文献[5、6]对具有不同丢失观测率的多传感器系统,在线性最小方差意义下,分别给出了集中式和分布式融合算法。但文献[4-6]没有考虑系统的不确定性。对带乘性噪声的系统,文献[7]利用线性矩阵不等式方法研究了线性离散系统的估计和控制问题。文献[8、9]分别对单传感器和多传感器系统,在线性最小方差意义下设计了最优估值器和集中式融合估值器。文献[10]研究了带乘性噪声系统的鲁棒滤波问题。然而,文献[8-10]没有考虑外界未知干扰的影响。
以上文献均分别对带有未知输入、观测丢失或乘性噪声系统开展的研究工作。但同时考虑以上诸多不确定性的文章鲜见。同时,由于多传感器信息融合可以克服单一传感器在时间和空间的限制,而在目标跟踪、导航和工业监测等领域具有广泛应用。集中式融合将每个时刻得到的原始观测数据,直接送到融合中心进行融合,具有全局最优性。因此,本文应用线性无偏最小方差准则,对同时带未知观测输入、观测丢失和乘性噪声的多传感器随机不确定系统,其中没有未知观测输入的任何先验信息,观测丢失用一组满足Bernoulli分布的随机变量描述,随机不确定性由不相关的乘性噪声表示,提出了集中式融合滤波算法。
1 问题阐述
考虑带未知观测输入、乘性噪声和观测丢失的多传感器随机不确定系统:
(1)
(2)
其中,系统状态为x(t)∈Rn;观测输出为yi(t)∈Rmi,i=1,2,…,L;系统噪声w(t)∈Rr与观测噪声vi(t)∈Rmi,i=1,2,…,L,是相关白噪声;状态乘性噪声ξ(t)∈R与观测乘性噪声λi(t)∈R,i=1,2,…,L,是与其他随机变量不相关的标量白噪声,均值为零,方差分别为Qξ(t)和Qλi(t);{γi(t)},i=1,2,…,L,是表示观测丢失的满足Bernoulli分布的随机噪声序列,概率分布为Prob{γi(t)=1}=αi,Prob{γi(t)=0}=1-αi,0≤αi≤1,γi(t)=1表示观测数据没有丢失,γi(t)=0表示观测数据丢失,该序列不相关于其他随机变量;θi(t)∈Rpi为未知观测输入干扰;Φ0(t),Φ1(t),Γ(t),H0i(t),H1i(t)和Di(t)是适当维数的时变矩阵,下标i表示第i个传感器,L为传感器的个数。
假设1 w(t)和vi(t)是零均值相关白噪声,方差阵和协方差阵为:
(3)
其中,Qvii(t)=Qvi(t)>0,δtk是Kroneckerdelta函数,即δtt=1,δik=0{δtt=0(t≠k)},E表示均值,T表示转置。
假设2 初始状态x(0)与ξ(t),λi(t),γi(t),w(t)和vi(t)不相关,且满足
(4)
假设3rank[Di(t)]=pi,mi>pi,i=1,2,…,L。rank[*]表示矩阵*的秩。

2 集中式融合滤波器
首先,对系统状态方程进行如下转换:
(5)
其中
(6)
易得W(t)的期望和方差分别为
(7)
则由(5)和(6)易知状态二阶矩矩阵X(t)=E[x(t)xT(t)]可如下计算:
(8)
系统(2)在假设1-假设3下,具有多传感器增广观测方程:
(9)
其中
(10)
其中,Imi表示mi×mi维的单位矩阵。
由于不知道观测干扰θc(t)的任何先验信息,对系统(1)和(9),笔者设计如下不依赖于未知干扰θc(t)的Kalman形式的集中式融合滤波器:
(11)
下面的定理给出了计算增益矩阵Fc(t)和Lc(t+1)的公式。
定理1 在假设1-假设3下,系统(1)和(9)的集中式融合滤波器(11)的系数矩阵Fc(t)和Lc(t+1)由下列公式计算:
(12)
(13)
其中
(14)
(15)
(16)
(17)
滤波误差方差阵Pc(t+1)计算为:
(18)

证明:由(1)和(11)有集中式融合滤波器的滤波误差方程:
(19)
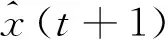
(20)
(21)
将(20)与(21)代入(19),滤波误差方程可整理为:
(22)
进一步,由(22)可求出集中式滤波器的滤波误差方差阵Pc(t+1)为:
(23)
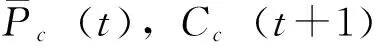
(24)
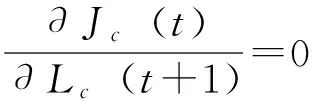
(25)
又Lc(t+1)Dc(t+1)=0,则有:
(26)
由Cc(t+1)可逆和Dc(t+1)列满秩,可知式(26)左边的矩阵可逆,利用假设3和矩阵求逆引理,可求出式(13)和式(15)。证毕。
3 仿真研究
考虑带未知观测输入、观测丢失和乘性噪声的3传感器随机不确定系统(1)-(2),系统噪声w(t)与观测噪声vi(t)相关,满足如下关系式vi(t)=ciw(t)+δi(t),i=1,2,3。w(t)和δi(t)为零均值、方差分别为Qw和Qδi的不相关高斯白噪声,ci为相关系数。仿真中取与文献[10]相同的状态参数:
其他参数取:
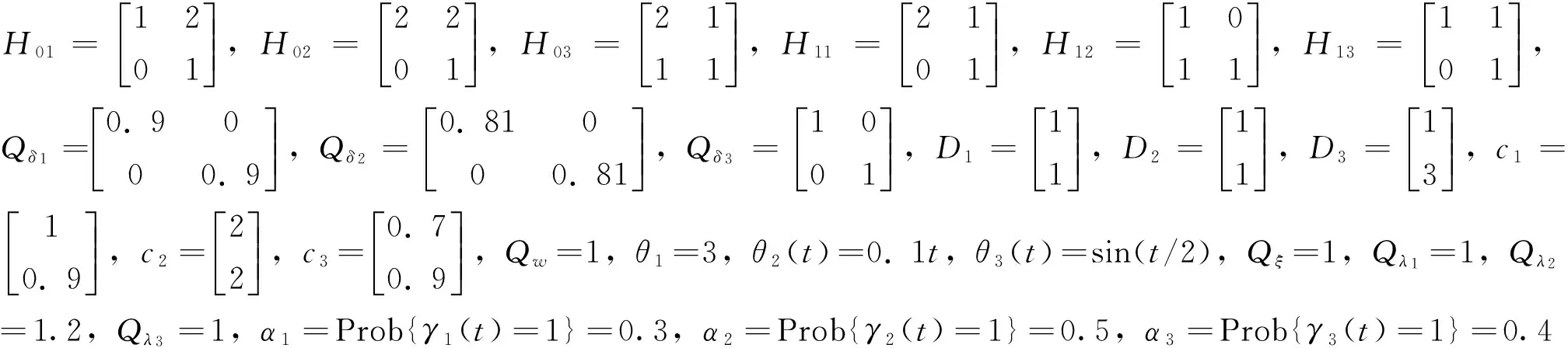
目的是求集中式融合滤波器,并与各局部滤波进行比较。为了验证算法的正确性给出200次Monte-Carlo实验的结果。
仿真结果如下:集中式融合滤波器跟踪曲线图见图1,其中,实线代表真实值,虚线代表滤波值,由图1可见,所提出的滤波器具有较好的跟踪性能。集中式融合滤波器和3个局部传感器的MSE比较图见图2,由仿真图可见,集中式融合滤波器的精度高于各局部滤波器的精度,符合理论结果。同样的参数条件下,由200次Monte-Carlo仿真实验得到的本文集中式融合滤波器(考虑未知观测输入)和文献[10]集中式融合滤波器(未考虑未知观测输入)的均方误差(MSEs)比较结果见图3,由图3可见,考虑了未知观测输入的影响,因而具有更高的精度。
4 结 论
本文对含有未知观测输入、观测丢失和乘性噪声的多传感器随机不确定系统,在不知道未知输入的任何先验信息的情况下,应用线性无偏最小方差准则推导了不依赖于未知观测输入的具有Kalman滤波器形式的集中式融合滤波器。
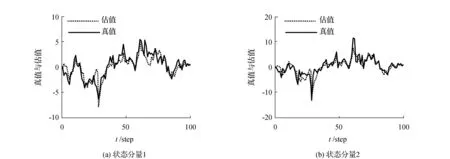
图1 集中式融合滤波器跟踪图Fig.1 Tracking performance of the centralized fusion filter
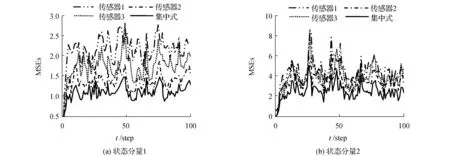
图2 局部和集中式融合滤波器的均方误差比较Fig.2 Comparison of the MSEs for the local and centralized fusion filters
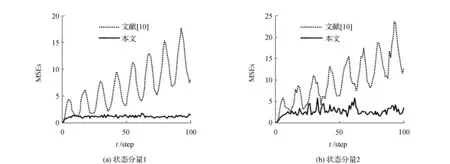
图3 本文和文献[10]集中式融合滤波器MSE比较Fig.3 Comparison of the MSE of centralized fusion filters in this paper and Ref.[10]
[1]GillijnsS,MoorBD.Unbiasedminimum-varianceinputandstateestimationforlineardiscrete-timesystemswithdirectfeedthrough[J].Automatica,2007,43(5):934-937.
[2]屈冬梅,马 静,孙书利.带未知输入随机奇异系统多传感器分布式融合滤波[C]//第二十九届中国控制会议.北京:北京航空航天大学出版社,2010:1 431-1 435.
[3]杨俊起,朱来芳.状态估计与未知输入和可测噪声同时重构方法[J].控制与决策,2013,28(8):1 145-1 151.
[4]NahiNE.Optimalrecursiveestimationwithuncertainobservation[J].IEEETransactionsonInformationTheory,1969,15(4):457-462.
[5]SunSL,LiXY,YanSW.Estimatorsforautoregressivemovingaveragesignalswithmultiplesensorsofdifferentmissingmeasurementrates[J].IETSignalProcessing,2012,6(3):178-185.
[6]ZhangT,MaJ,SunSL.Distributedfusionfilterfordiscrete-timestochasticsystemswithuncertainobservationandcorrelatednoises[C]//Proceedingsofthe8thIEEEInternationalConferenceonControlandAutomation,2010:704-708.
[7]LiWW,TodorovE,SkeltonRE.Estimationandcontrolofsystemswithmultiplicativenoisevialinearmatrixinequalities[C]//ProceedingsoftheAmericanControlConference,2005,3:1 811-1 816.
[8]MaJ,SunSL.Optimallinearestimationforsystemswithmultiplicativenoiseuncertaintiesandmultiplepacketdropouts[J].IETSignalProcessing,2012:839-848.
[9]MaJ,SunSL.Centralizedfusionestimatorsformulti-sensorsystemswithmultiplicativenoisesandmissingmeasurements[J].JournalofNetworks,2012,7(10):1 538-1 545.
[10]MohamedSMK,NahavandiS.Robustfinite-horizonKalmanfilteringforuncertaindiscrete-timesystems[J].IEEETransactionsonAutomaticControl,2012,57(6):1 548-1 552.
[11]方保镕,周继东,李医民.矩阵论[M].北京:清华大学出版社,2004:358-364.
Centralized fusion filtering for stochastic uncertain systems with unknown measurement inputs and missing measurements
PANG Chong-Yan,SUN Shu-Li*
(School of Electronic Engineering,Heilongjiang University,Harbin 150080, China)
A centralized fusion filter is designed for a multi-sensor stochastic uncertain system with unknown measurement inputs and missing measurements.The stochastic uncertainties are described by multiplicative noises existing in the state and measurement matrices of systems.A Kalman-like centralized fusion filter independent of unknown inputs is given by using the linear unbiased minimum variance criterion in the case that no prior information about unknown inputs is available.A simulation example shows the effectiveness of the algorithms.
unknown input;missing measurements;multiplicative noise;centralized fusion filter;linear unbiased minimum variance
10.13524/j.2095-008x.2015.02.033
2015-03-30
国家自然科学基金资助项目(61174139);黑龙江省杰出青年基金资助项目(JC201412)
逄崇雁(1989-),女,黑龙江佳木斯人,硕士研究生,研究方向:状态估计,E-mail:pangchongyan@126.com;*通讯作者:孙书利(1971-),男,黑龙江伊春人,教授,研究方向:状态估计、信号处理、信息融合、传感器网络等,E-mail:sunsl@hlju.edu.cn。
TP274.2
A
2095-008X(2015)02-0074-06
