变截面钢支撑滞回性能研究
2015-03-17刘洪波曹正旺邵永松刘晓丽柳艳杰
刘洪波,曹正旺,邵永松,刘晓丽,柳艳杰
(1.黑龙江大学 建筑工程学院,哈尔滨 150080;2.哈尔滨工业大学 建筑设计研究院,哈尔滨 150090;3.黑龙江省民族职业学院,哈尔滨 150066)
变截面钢支撑滞回性能研究
刘洪波1,2,曹正旺1,邵永松2,刘晓丽3,柳艳杰1
(1.黑龙江大学 建筑工程学院,哈尔滨 150080;2.哈尔滨工业大学 建筑设计研究院,哈尔滨 150090;3.黑龙江省民族职业学院,哈尔滨 150066)
为改善铰接钢支撑受压稳定性从而提高受压承载力,将支撑设计成两端小中间大的变截面构件,通过增大支撑中部截面尺寸,使支撑在受压时塑性区域向两端外移,形成更大范围的塑性区,更有利于其在地震作用下的耗能。利用有限元分析方法研究工形截面、方钢管截面和圆钢管截面的变截面支撑的滞回性能。研究表明在保证支撑构件满足规范要求的宽厚比前提下,支撑长细比和楔率是影响变截面支撑滞回性能的主要因素,变截面支撑初始轴向刚度、承载能力、耗能性能随楔率增大而增大。
钢支撑;变截面;滞回性能
0 引 言
钢支撑体系由于其构造简单,可有效地限制结构的侧向变形,是建筑结构抗侧力体系中一种最常见的,在多高层钢结构建筑中应用广泛。钢支撑根据支撑轴线是否通过梁柱交点又分为中心支撑和偏心支撑。中心支撑可为钢框架提供较大抗侧刚度,有效限制结构在地震作用下的侧向变形,但是中心支撑容易发生受拉屈服和受压失稳,支撑失稳后承载力快速降低,支撑无法继续承担荷载,同时也不利于结构的耗能[1];偏心支撑同时具有良好的延性和耗能能力,但在地震作用下只有耗能梁段处能发挥其非线性行为,使得耗能梁段变形大,震后结构维护困难,同时耗能梁段计算复杂[2]。
本文根据铰接钢支撑在小偏心受压时杆中弯矩和变形最大、杆端弯矩和变形为零[3]的受力特点提出一种受力明确、构造简单的变截面全钢中心支撑,并对其滞回性能进行研究,分析其承载能力与耗能能力。
1 建立有限元模型
研究支撑滞回性能的模型主要分为:塑性铰模型、现象学模型、有限元模型[4]。由于塑性铰方法和现象学方法无法考虑支撑截面尺寸沿轴线方向的变化,为研究变截面支撑的抗震性能,本文利用ANSYS有限元程序对3种截面形式变截面支撑(工形截面、方钢管截面和圆钢管截面)在低周循环荷载作用下的受力性能进行研究,研究支撑屈曲后承载力及支撑耗能。在进行变截面支撑滞回性能研究时,控制端部截面相同,通过改变楔率,研究楔率对变截面支撑滞回性能的影响,研究不同楔率变截面支撑在低周循环荷载作用下的受力性能[5]。本文采用均匀增幅位移加载方式来研究变截面支撑的滞回性能。定义γ为变截面支撑的楔率,由下式计算:
式中b1、b0分别为支撑中部截面、端部截面翼缘宽度。
利用ANSYS有限元分析软件中SHELL181单元建立不同参数的变截面支撑模型,选用Q235钢材,弹性模量E=2.06×105MPa,切线模量Es t=0.02E,屈服应力σy=235 MPa,泊松比ν=0.3,采用双线性随动强化法则及Von Mises屈服准则,按照构件在第一局部屈曲模态下的屈服形式,对支撑中部施加截面外径1/1 000的局部初始缺陷,按照构件在第一整体屈曲模态下的屈服形式,对模型整体施加支撑长度1/1 000的整体初始缺陷。由于构件残余应力仅影响滞回曲线中初次受压的最大值,随后由于支撑被反复受压屈曲和拉直屈服,构件内部发生应力重分布,使残余应力不再影响支撑的滞回性能[6]。因此,本文不考虑残余应力的影响。
2 变截面支撑滞回性能研究
2.1 工形变截面支撑滞回性能
利用ANSYS有限元分析软件模拟工字形变截面支撑在低周循环荷载作用的受力,比较端部截面相同时变截面支撑的滞回性能[7]。共选取了4个截面,构件截面尺寸见表1,其中H-1为等截面支撑,H-2、H-3、H-4为变截面支撑。

表1 工形变截面支撑构件几何参数表
构件在低周循环荷载作用下的滞回曲线见图1。图1横坐标为支撑端部轴向位移Δ与支撑单调加载达极限荷载时端部位移Δy的比值,纵坐标为荷载P与支撑端部全截面屈服荷载Poy的比值(受压为正),虚线为单调加载曲线。

图1 H组试件滞回曲线Fig.1 Hysteretic curves of H groups
由图1可见,在弹性范围内,滞回环面积几乎为零,支撑不参与耗能;支撑构件进入屈服阶段,支撑因塑性变形逐渐开始耗能,每级荷载循环3次后支撑承载力趋于稳定,且支撑强度随循环次数增多有所降低。
试件承载力经多次循环加载后相比单调加载均有所降低;拉应力状态下,由于构件未发生平面外位移,支撑轴向刚度几乎没有发生变化;压应力状态下,由于构件发生侧向变形,支撑轴向刚度随加载幅值的增大而逐渐变小,当压应力卸载完毕后逐步施加拉应力,支撑轴向刚度随拉应力的增大逐渐恢复。
各试件滞回环总面积见图2。图2横坐标为循环加载圈数,纵坐标为滞回曲线累计面积(无量纲)。

图2 H组试件滞回环面积Fig.2 Hysteretic loop area of H groups
由图2可见,滞回环面积随着加载圈数增多而增大,说明支撑耗能逐渐增多;当加载圈数相同时随楔率增大,滞回环面积逐步增大。
2.2 方钢管变截面支撑滞回性能
与工字形变截面支撑滞回性能研究方法相似,方钢管变截面支撑的滞回性能同样使用ANSYS有限元分析软件[8],模拟方钢管变截面支撑在低周循环荷载作用下的受力,比较端部截面尺寸相同时变截面支撑的滞回性能。共选取了4个截面,构件截面尺寸见表2,其中F-1、F-3、F-4为变截面支撑,F-2为等截面支撑。
方钢管变截面支撑试件在低周循环荷载作用下的滞回曲线见图3。图3滞回曲线受压为正,虚线为单调受压加载曲线。

表2 方钢管变截面支撑构件几何参数表

图3 F组试件滞回曲线Fig.3 Hysteretic curves of F groups
观察滞回曲线可知,与工形变截面支撑相似,方钢管变截面支撑的滞回曲线特征:幅值相同时,支撑承载力随加载圈数增多而降低;在拉应力状态下,与支撑初始轴向刚度相比,支撑轴向刚度基本未变,在压应力状态下,支撑轴向刚度有所降低;变截面支撑承载力随着楔率增大逐渐提高,且其滞回曲线逐渐饱满。
各试件滞回环总面积见图4。图4横坐标为循环加载圈数,纵坐标为滞回曲线累计面积(无量纲)。
观察图4中曲线可见:循环加载圈数相同时,变截面支撑累计耗能相比等截面支撑大幅提高,且随楔率增大,变截面支撑耗能能力越强,例如:当楔率均为0.5时,F-3试件相比F-2试件耗能提高93.41%。
2.3 圆钢管变截面支撑滞回性能
选取不同截面参数的圆钢管变截面支撑与等截面支撑,研究其在低周循环荷载作用下的受力性能[9],试件截面参数见表3。表3中组别Y-1、Y-3、Y-4为变截面试件,Y-2为等截面试件。
2.3.1 滞回曲线
圆钢管变截面支撑荷滞回曲线见图5。图5受压为正,虚线为单调受压加载曲线。

图4 F组试件滞回环总面积Fig.4 Hysteretic loop area of F groups

表3 圆钢管变截面支撑构件几何参数表

图5 Y组试件滞回曲线Fig.5 Hysteretic curves of Y groups
由图5可见:与工字形变截面支撑、方钢管变截面支撑相似,圆钢管变截面支撑滞回曲线具有以下特征:加载幅值相同时,随加载圈数增多支撑承载力降低;在拉应力状态下,与支撑初始轴向刚度相比,支撑轴向刚度基本未变;在压应力状态下,支撑轴向刚度较初始轴向刚度;变截面支撑承载力随着楔率增大逐渐提高,且其滞回曲线逐渐饱满[10]。
各试件滞回环总面积见图6。图6横坐标为循环加载圈数,纵坐标为滞回曲线累计面积(无量纲)。
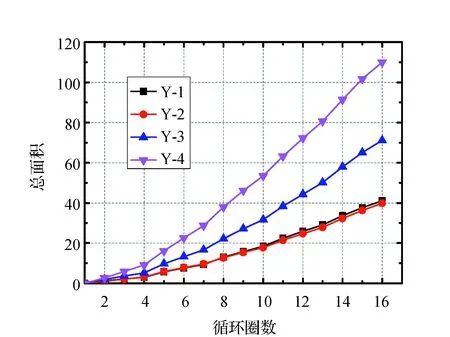
图6 Y组试件滞回环总面积Fig.6 Hysteretic loop area of Y groups
由图6可见:循环加载圈数一定时,支撑总耗能随楔率增大而逐渐增多;楔率一定时,小长细比变截面试件总耗能较等截面试件提高,例如:当楔率均为0.5时,Y-3试件较Y-2试件提高78.55%。
3 结 论
本文研究了3种截面形式(工字型、方钢管、圆钢管)的变截面支撑在低周往复循环荷载作用下的受力性能,比较长度及端部截面尺寸相同时不同
楔率变截面支撑的滞回性能,并得到以下结论:
1)在满足规范要求的支撑板件宽厚比前提下,支撑楔率及长细比是影响变截面支撑滞回性能的主要因素。
2)构件长度、端部截面尺寸相同时,随楔率不断增大,变截面支撑初始轴向刚度逐步增大;在循环荷载作用下,变截面支撑承载力相比等截面支撑大幅提高,其能量耗散能力大为改善,且随着楔率增大耗能能力更强;在满足支撑平面外稳定的前提下,楔率范围可扩展更大,楔率甚至可大于1。
[1]马 宁.全钢防屈曲支撑及其钢框架结构抗震性能与设计方法[D].哈尔滨:哈尔滨工业大学,2010:1-15.
[2]罗亚男.K型偏心支撑钢框架弹塑性受力性能研究[D].西安.西安科技大学,2013.
[3]Dinnik A H.纵向弯曲与扭转[M].谢贻权译.上海:上海科学技术出版社,1962:75-104.
[4]黄明泽,连尉安.钢支撑滞回试验及模拟方法探索[J].低温建筑技术,2009,7:52-54.
[5]李 莹.中心支撑框架结构及钢支撑滞回曲线模拟[J].科技创新导报,2012,25:111-113.
[6]申 林.高层钢结构钢支撑滞回性能分析及抗震设计对策[D].西安:西安建筑科技大学,2000:50-52.
[7]于海丰,张文元,张耀春.Q235焊接工字形钢支撑的低周疲劳性能试验及数值模拟[J].四川大学学报:工程科学版,2012,(2):182-190.
[8]赵宝成,于安林,王军良,等.内填Y形钢支撑加固多层钢筋混凝土框架结构滞回性能试验研究[J].建筑结构学报,2013,(8):107-118.
[9]白 翔,吕玉彬,白补林,等.变截面轻型门式刚架拼接处设计方法研究[J].中国安全生产科学技术,2013,(1):51-57.
[10]孙学水,王 湛,胡淑军,等.新型耗能支撑的试验研究和有限元分析[J].建筑钢结构进展,2014,(3):24-29.
Hysteretic behavior of variable cross-section steel brace
LIU Hong-Bo1,2,CAO Zheng-Wang1,SHAO Yong-Song2,LIU Xiao-Li3,LIU Yan-Jie1
(1.College of Civil Engineering,Heilongjiang University,Harbin 150080,China;2.The Architectural Design and Research Institute of Harbin Institute of Technology,Harbin 150090,China;3.Heilongjiang Vocational College for Nationalities,Harbin 150066,China)
In order to strengthen the stability of the steel braced frame with pinned connections thus enhance the bearing capacity,the braces were designed in variable cross section which great in the middle and little at both ends.It has been noticed that the expansion of the middle section area making the braces plastic zone shifted towards both ends under the force of pressure.As a result,a larger plastic zone formed.The I-section,circular hollow and rectangular hollow variable cross-section braces hysteretic behavior was investigated by finite element method.The results indicate that in braces width-thickness ratio meets standard requirements,the main factors affecting variable cross-section braces hysteretic behavior are the slenderness ratio and the wedge ratio.Wedge ratio is the larger,capacity of initial axial rigidity,carrying capacity and energy dissipation are the better.
steel brace;variable cross-section;hysteretic behavior
10.13524/j.2095-008x.2015.02.019
2014-11-13;
2014-12-06
黑龙江省教育厅科学技术研究项目(12531482);黑龙江大学杰出青年科学基金资助项目(JCL201104);中国博士后科学基金资助项目(20110491076)
刘洪波(1976-),男,黑龙江鸡东人,教授,博士,研究方向:高层钢结构和建筑智能材料,E-mail:interdage@163.com。
TU973.13
A
2095-008X(2015)02-0001-06
