孔隙结构渗透性能的数值模拟研究

刘 阳，赵起超

(煤炭工业郑州设计研究院股份有限公司，河南 郑州 450007)



孔隙结构渗透性能的数值模拟研究

刘 阳，赵起超

(煤炭工业郑州设计研究院股份有限公司，河南 郑州 450007)

以渗透系数为评价指标，利用ANSYS有限元程序模拟孔隙结构的孔隙率和平均孔径对其渗透性能的影响。通过建立渗流仿真模型计算不同孔隙率、不同孔径对应的等效渗透系数，并拟合数学表达式来分析孔隙率、孔径对孔隙结构渗透系数的影响程度。结果表明：孔隙结构的等效渗透系数与孔隙率呈线性正相关关系，与平均孔径呈二次幂函数正相关关系。

孔隙结构；渗透系数；孔隙特征

孔隙结构特征包括孔隙的孔隙率、平均孔径、孔喉比以及孔隙结构的贯通度。根据压汞试验显示，液体能够进入的孔径的大小与进液压力有关，也就是说孔径的大小影响孔隙结构渗流的难易程度，孔喉比就是孔径与孔道尺寸的相对比值，孔喉比较大时也是影响渗透系数的关键因素[1]。按孔隙体的发育程度将孔隙分成贯通孔隙、“盲端”孔隙和“死”孔隙三种类型[2]。“死”孔隙在孔隙体中孤立的存在，两端均不与其他孔相连；“盲端”孔隙只有一端与其他孔相连；贯通孔隙至少与两个孔连接。“盲端”孔隙仅仅在初始渗流期起贮存流体的作用，在后期的“饱和”渗流期对孔隙渗流的影响就会很小。本文仅针对贯通孔隙的孔隙特征进行分析。

1 二维孔隙渗流的ANSYS模拟

通过对比发现，在一定温差下的热传导与在一定水头下的渗流的数学表达式很相似。首先达西定律和热传导定律很相近，其次是渗流场和温度场的微分方程及边界条件相似。

根据这两大物理场的近似性[3]，利用ANSYS数值分析软件模拟水在孔隙体中的渗流。数值计算过程：用温差T来代表渗透压差H，用导温系数a来代表导流系数b，用热流密度tf来代表水的流速v，用热流梯度tg来代表水力梯度J。从而，把导热问题转化为水的渗流问题求解。

1.1 二维孔隙渗流模型

很多学者研究了规则孔隙分布状态下混凝土的渗透特征[1]，为了验证混凝土渗透特征的有效性，需要进一步进行随机孔隙分布的渗透试验模拟。孔隙的分布基于随机理论的蒙特卡洛方法，在一个预定的孔隙率下随机布置[4]。在固定孔隙率的情况下，孔隙位置随机分布。建立的结构体模型为：确定结构的孔隙率为30%，绿色颗粒为孔隙单元，红色颗粒为固相单元。利用该模型来模拟二维多孔结构的稳态渗流(见图1、图2)。

1.2 二维孔隙渗透模型的设置

1.2.1 二维孔隙模型的基本假定

1) 假定所有空隙都为贯通的有效空隙，不存在盲端孔隙；

2) 假定渗透系数各向同性；

3) 孔隙单元的渗透系数的取值按照等开度平滑孔隙渗透系数计算公式确定[4]。

图1 多孔介质孔隙分布

图2 结构体加载情况

1.2.2 二维孔隙渗流的边界条件

1) 上下边界为隔水边界；

2) 右边界水头压力为H0=100 m；

3)左边界为自由边界，水头压力为0 m。

1.3 二维孔隙渗流场模拟结果

1.3.1 二维孔隙的渗流场的等值线图

从图3和图4可以看出：该孔隙结构二维有限元模型的渗流速度和水力梯度除了在邻近单元之间存在渗流场的变化外，还受其他层位孔隙渗流的影响。渗流速度和水力梯度呈现非均匀性，因此该渗流模型属于二维渗流。

图3 渗流速度等值线图

图4 水力梯度等值线图

从图3看出，多孔结构的渗流速度在整个渗流断面内是不均匀分布的，在孔隙通道处，渗流速度最大，固相单元渗流速度最小。

1.3.2 二维孔隙渗流渗透系数的计算

由达西定律计算孔隙结构的渗透系数为K=V/J=V/(ΔP/L)，式中：V为水的流速，m/s；J为水力梯度，MPa/m。对该渗流断面上的各个单元的渗透系数进行计算，进而求得孔隙结构该渗透断面上的“等效”渗透系数[4]。

通过上述数值模拟的等值线图看出，渗流速度v和水力梯度J呈现竖向明显的随机性。在计算孔隙体的整个渗流断面的“等效”渗透系数时，须选取整个断面上的所有单元参与计算。

2 渗透系数的影响因子分析

为了通过数值模拟得出渗透系数k与孔隙率φ、孔径Lp的关系，弄清楚孔隙结构渗流的影响因子对渗透系数的影响程度，按照表1和表2安排孔隙结构渗流模拟试验，并按上述计算公式计算出不同孔隙状态下的等效渗透系数。

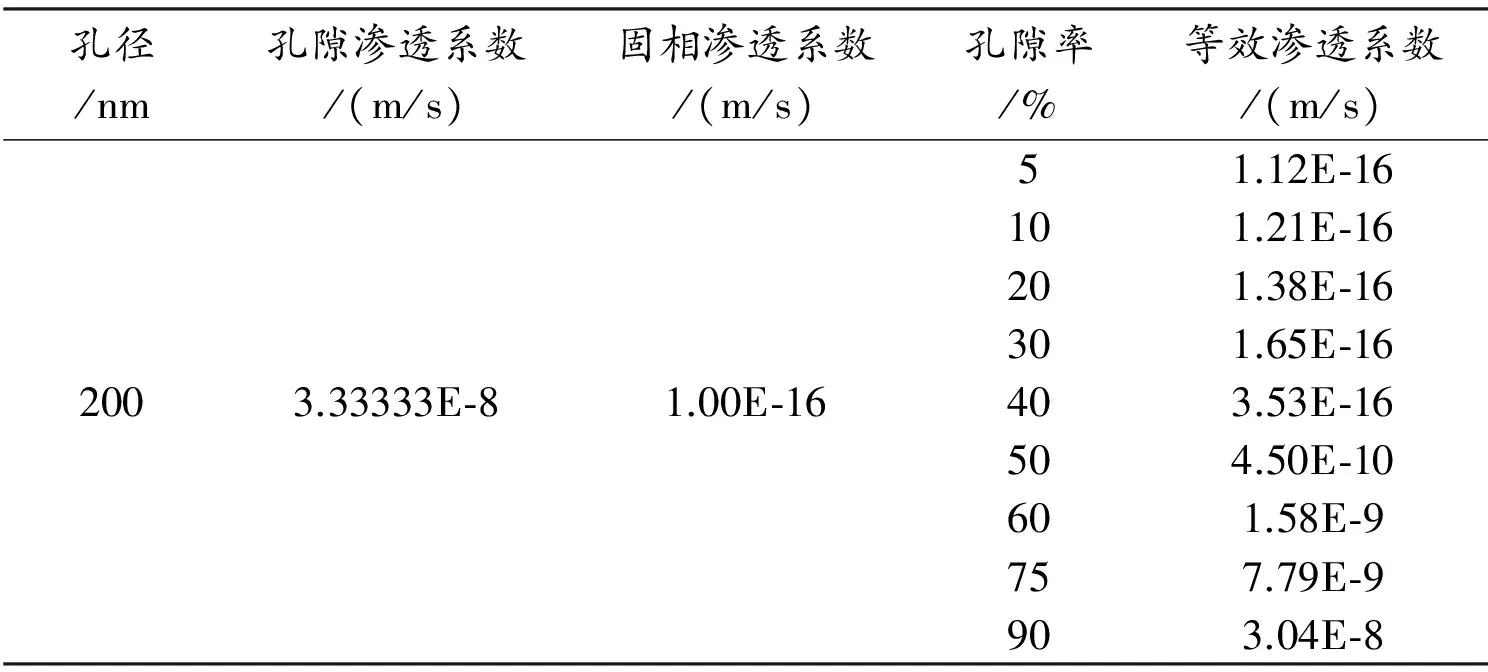
表1 孔隙率-渗透系数的关系

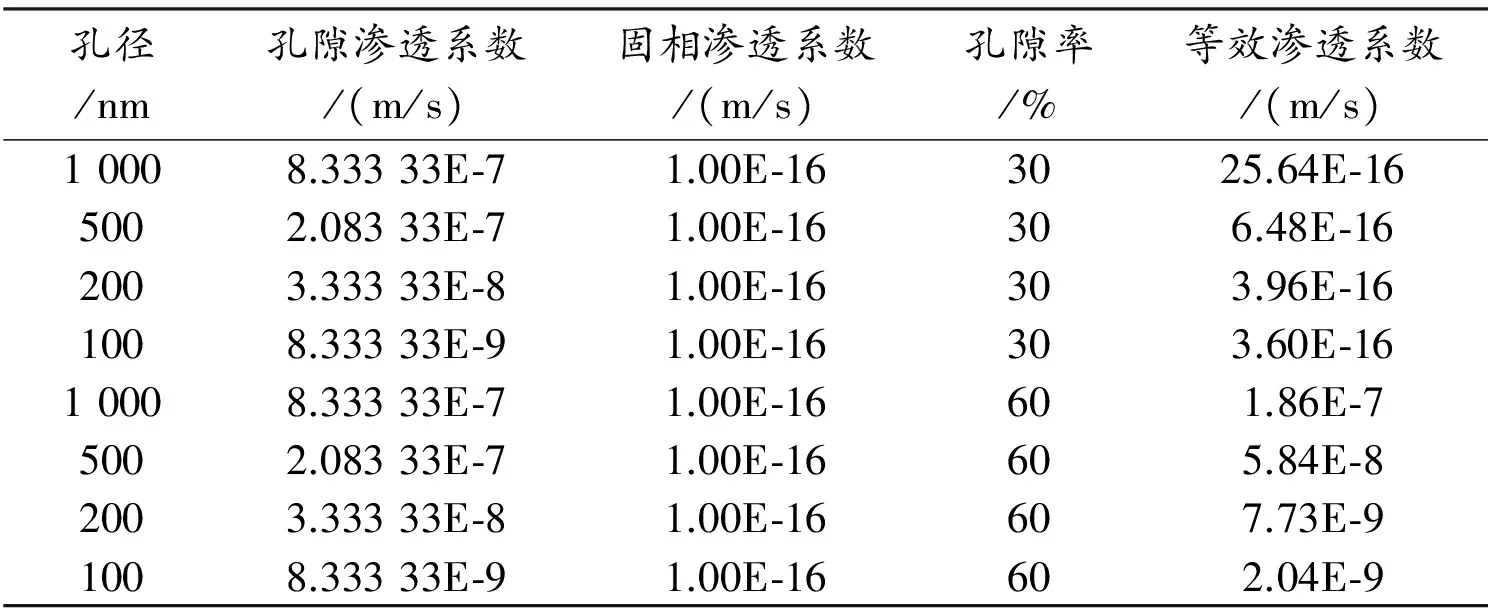
表2 平均孔径-渗透系数的关系

2.1 渗透系数k与孔隙率φ的关系

由图5和图6看出：混凝土的孔隙率在0～40%之间时，渗透系数与孔隙率基本呈线性正相关关系。二者满足k=2.088 1φ+1.000 7的关系，R2接近于1，说明二者线性相关性非常高，曲线拟合的精度满足要求。孔隙率在40%～50%之间，渗透系数发生突变；混凝土的孔隙率在50%～90%之间时，渗透系数与孔隙率基本呈线性正相关关系。

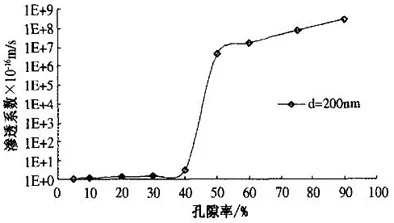
图5 孔隙率-渗透系数关系(a)

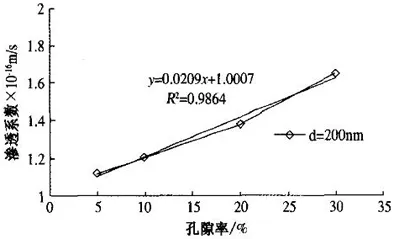
图6 孔隙率-渗透系数关系(b)

2.2 渗透系数k与孔径Lp的关系

由图7和图8看出：混凝土的孔隙率固定，渗透系数随孔径增大而增大，二者大致呈二次幂正相关关系。这一结论与Ergun(厄根)方程相吻合，说明随机孔隙渗流模拟试验结果的可靠性很高。

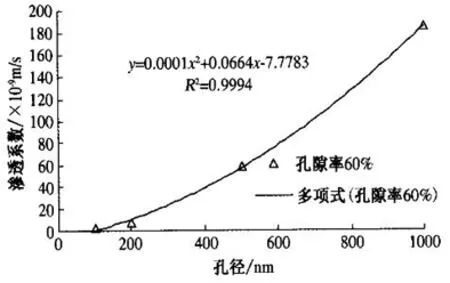
图7 孔隙率60%时渗透系数随孔径变化

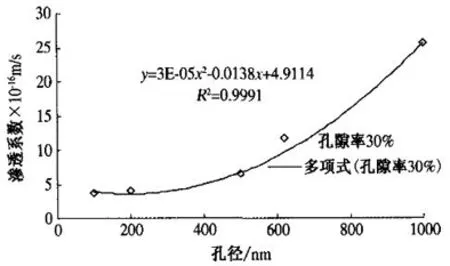
图8 孔隙率30%时渗透系数随孔径变化

3 结论

(1)孔隙结构的渗透系数与其孔隙率呈线性正相关关系；这一点无论是规则孔隙分布的渗流结果还是随机分布的孔隙渗流结果，都具有这一显著特征，并且同现有的Ergun(厄根)方程相符合。随机模拟结果还发现，多孔介质的渗透系数随着孔隙率增加到一定程度，会出现一个突变的现象，然后又趋向规律化。

(2)孔隙结构的渗透系数与其孔径呈二次幂函数正相关关系，与Ergun(厄根)方程相吻合，说明随机孔隙模拟试验结果的可靠性很高。

(3)孔隙结构的渗透系数与孔隙率和平均孔径密切相关，研究孔隙结构的渗透性能，同时还须从孔隙结构的微观结构入手研究孔隙分形特征[5-6]，本文没有对此展开研究。

[1]刘阳，乔熙，张鹏．多孔介质渗透系数的数值模拟研究[J].徐州建筑职业技术学院学报，2010，10(4)：8-12．

[2]叶礼友．基于N-S方程的多孔介质微观渗流数值模拟[D].武汉：武汉工业学院，2008．

[3]余雄杰，邱勇.三维有限元渗流模拟计算在水库安全评价中的应用研究[J].吉林水利，2008(3)：20-22.

[4]李守巨，上官子昌，孙伟，等．多孔岩土材料渗透系数与孔隙率关系随机模拟[J]．辽宁工程技术大学学报，2010，29(4)：589-592．

[5]刘阳，贾俊超，王磊．多孔结构孔隙特征的分形研究[J].河南城建学院学报，2011(1)：33-36．

[6]李留仁，赵艳艳，李忠兴，等. 多孔介质微观孔隙结构分形特征及分形系数的意义[J].石油大学学报，2004,28(3)：105-107.

Numerical simulation research on pore structure’s Permeability

LIU Yang, ZHAO Qi-chao

(ZhengzhouCoalIndustryDesignandResearchInstituteCo.,Ltd.,Zhengzhou450007,China)

Taking permeability coefficient as assessment?criteria, ANSYS finite element program is used to simulate the effect caused by porosity of pore structure and average pore diameter on permeability. Calculation of different porosity, pore size different permeability coefficient are made through the establishment of a simulation model, and the degree of influence is discussed based on fitting a mathematical expression analysis of porosity and pore size on the pore structure of the permeability coefficient. The results show that the equivalent permeability and porosity of the pore structure, as well as the average pore size have a positive linear correlation and correlated second power function respectively.

pore structure; permeability; porosity characteristics

2015-01-20

刘 阳(1983-)，男，河南驻马店人，硕士，助理工程师。

1674-7046(2015)02-0022-04

10.14140/j.cnki.hncjxb.2015.02.005

TU528

A