城市道路地下空洞病害发展机理及对路面塌陷的影响
2015-03-17陶连金袁松安军海
陶连金,袁松,安军海
(北京工业大学建筑工程学院,北京100124)
0 引言
近年来,我国各大城市道路空洞造成的路面塌陷事故频繁发生,给社会带来了巨大的经济损失。然而,道路地下空洞具有隐蔽性强、突发性强、引起原因众多、难以提前预测等特点,因此,研究其对城市道路路面塌陷的影响问题就显得十分必要。宋谷长等[1]分析了北京城市道路塌陷的特点与成因,并在此基础上提出相关对策。李智强[2]指出土层因素、管道渗漏和管道回填是引起城市道路路面塌陷的主要因素,并将城市地陷的发育过程分为细颗粒流失、隐伏土洞形成和临界塌陷状态三个阶段。高明生[3]对部分城市道路塌陷事故的原因和危害进行了统计分析并提出了预防措施。陈昌彦等[4-5]也分析了城市道路塌陷的成因。但这些研究均限于统计和概括分析,比较笼统。余乐[6]采用有限元软件模拟了空洞的角度和覆跨比对路基的影响。翟淑花[7]以刚性管和地下空洞为主体,运用FLAC3D建立三维数值模型,分析了空洞演化对管道位移场和应力场的影响,但有限元软件模拟土颗粒的运动有很大的局限性。为此,笔者基于离散元软件PFC2D,从土颗粒角度分析砂土路基下空洞的发展破坏机理,并定量给出地下空洞对路面塌陷的影响程度,以期为道路地下空洞病害的治理及路面塌陷预测提供依据。
1 地下空洞发展机理模拟
道路地下空洞发展机理的模拟基于离散元软件PFC2D。该软件适用于模拟颗粒介质的运动及固体颗粒流动问题的计算,可从微观角度反映空洞的变形发展过程,直观地揭示其破坏机制。图1给出了路面下地基中存在直径3 m、埋深2 m空洞的计算模型。图2给出了空洞从形成到发展直至路面发生塌陷的过程,其中,t为软件计算时步。

图1 计算模型Fig.1 Calculation model

图2 路面塌陷过程Fig.2 Process of road surface collapse
从图2中可以看出,空洞形成后,其顶部的部分松动颗粒开始掉落,并逐渐形成塌落区。计算到3.0×105步时,可以明显看出,空洞顶部土体逐渐形成梯形松动带。松动带两侧土体(呈三角形分布)逐渐振动密实,而塌落带土体不断脱落、下移,最终充实空洞,并完全脱离路基底面,形成路面下空洞区。施加路面超载后,面层发生弯折破坏,造成道路中断。
2 工程背景与数值模型
2.1 工程背景
北京市区道路多为4~15 cm沥青混凝土面层15~50 cm的水泥稳定砂砾或泥灰结碎(砾)石或工业废渣,路基底部土层多为人工堆积层、杂填土、黏质粉土、砂质粉土、粉细砂等,相对路面层刚度较小、整体性较差,与路面底部容易发生脱离,而形成松动或空洞带。
2.2 PFC2D数值模型
结合北京地区地层实际情况,在模拟时选取实际路基下的地基,路基为50 cm厚水泥稳定砂砾,路面为15 cm厚沥青混凝土。由于目前计算机速度和容量的限制,对模型的大小和颗粒的尺寸进行了优化试算[8]。
试样的尺寸为21.00 m×20.65 m,为了更加真实地模拟路面结构,将其分为三层结构,顶层为路面层,中间层为路基层,底层为土基层。颗粒单元半径从Rmin到Rmax均匀分布,模型的初始面积孔隙比为0.16,路面层采用平行接触模型,路基层为接触黏结模型。数值实验基本参数见表1,其中,I1、I2分别为颗粒法向接触刚度和颗粒切向接触刚度。

表1 模型试样基本参数Table 1 Basic parameters of model
定义边界[9-11],以上下左右四个墙体为边界围成指定的区域,定义的颗粒在此边界内随机生成。为了加快颗粒生成的效率,先生成比原半径小的颗粒,再乘以一个放大系数得到指定的颗粒半径,施加重力加速度,运算得到初始平衡状态。布置三个监测点,从上至下分别为路面层底部监测点、基层底部监测点和土基层顶部监测点,其水平位置为地下空洞中心对应位置。数值模型如图3所示。

图3 基本模型Fig.3 Basic model
通过数值模拟,分析地下空洞的规模D、埋深h、施工扰动振动波速度幅值v、路基土性因素,对道路破坏的影响趋势和程度,分析路基空洞在不同情况下的发展趋势。模拟工况参数见表2。
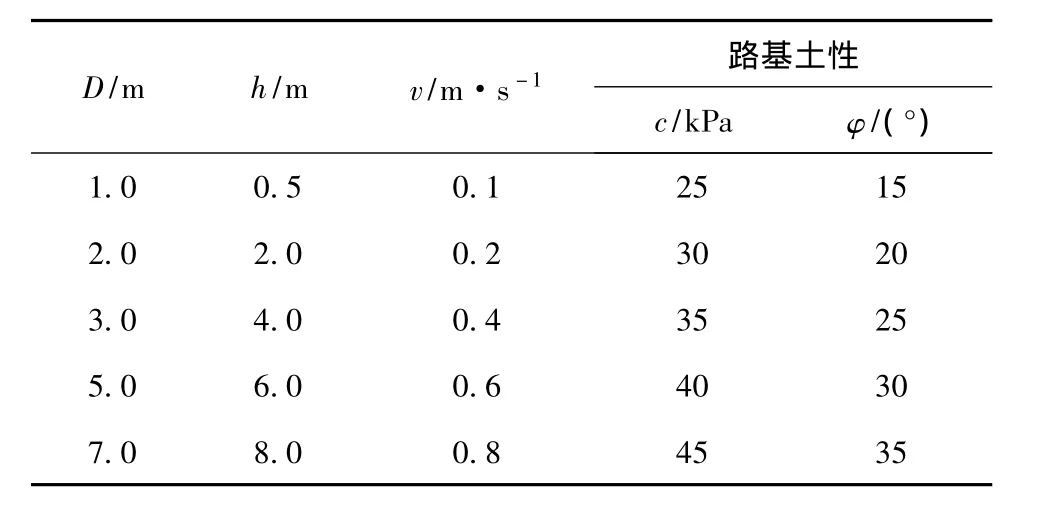
表2 模拟工况参数Table 2 Parameters of simulated condition
其中,施工扰动工况采用图4所示地铁施工中实测的振动波及其傅里叶谱确定,从模型底层输入的振动波速度幅值取为0.1、0.2、0.4、0.6、0.8 m/s。
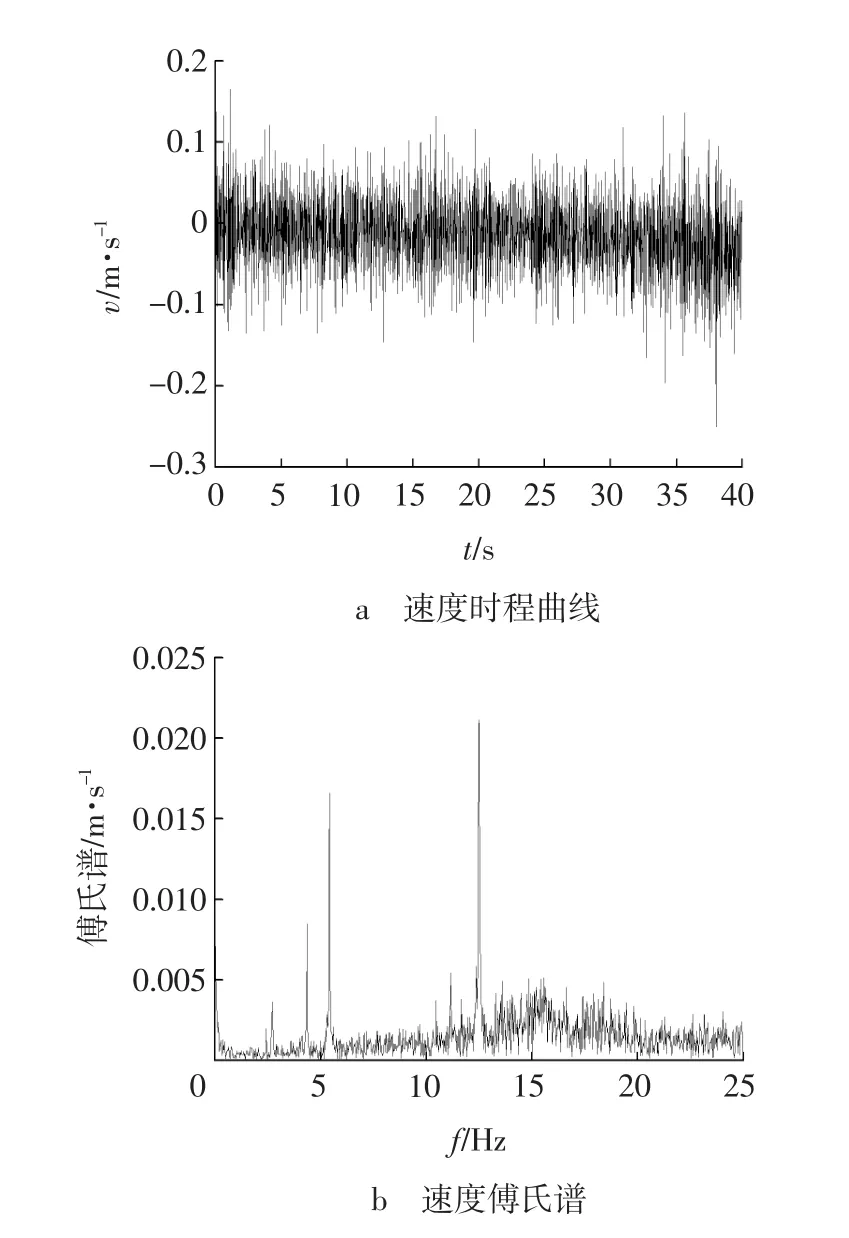
图4 施工扰动速度时程及其傅氏谱Fig.4 Time history of construction disturbance velocity and fourier spectrum
3 结果与分析
3.1 空洞规模对路面沉降的影响
图5给出了道路面层下伏不同空洞尺寸下的沉降值s,其中,数值模型的土层均为砂土,φ为25°。
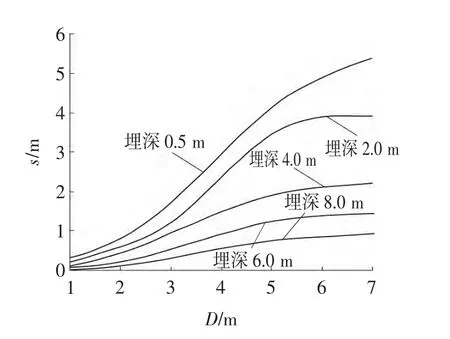
图5 空洞埋深与路面沉降关系Fig.5 Relationship of depth of cavity and surface subsidence
从图5可以看出,随着空洞尺寸的增加,沉降值明显逐渐变大,所以空洞大小是影响道路沉降变形的重要因素。当空洞直径小于3 m,面层沉降变形缓慢增加;当直径为3~6 m时,曲线斜率快速增加,其面层沉降也快速增长;当直径大于6 m时,面层沉降值趋于一个稳定值,这是因为面层已发生坍塌破坏,沉降变形值不再增长。因而针对特定的土层及空洞埋深,能找到一个影响道路面层破坏空洞尺寸的关键点,在本例中关键点为直径6 m。当直径大于6 m时,沉降值不再发生大的变化,路面发生坍塌,沉降达到稳定。

图6 空洞规模与路面沉降关系Fig.6 Relationship of scale of cavity and surface subsidence
3.2 空洞埋深对路面沉降的影响
为分析下伏空洞的埋深对道路安全性的影响,图6中给出了道路监测点在四种规模工况下处于不同埋深时的沉降变形值(土样为砂土,φ为25°)。
从图6中可以看出,对于不同直径的空洞计算工况,随着空洞埋深的增加,道路结构各监测点的沉降值均会迅速降低,降低的幅度大致呈现出先急速后变缓的趋势,直至最后出现一条平缓的直线,因而不同空洞直径工况下的沉降曲线一定会存在一个拐点。所以,对埋深因素下不同直径的工况进行统计分析时,应找出其拐点埋深,为相关设计和空洞治理提供参考。基于图6模拟结果,推荐拐点埋深为6 m。
3.3 施工扰动对路面沉降的影响
基本模型的土样为砂土,φ取25°,选用直径2 m、埋深2 m的空洞,分析施工扰动与面层沉降关系曲线,如图7所示。
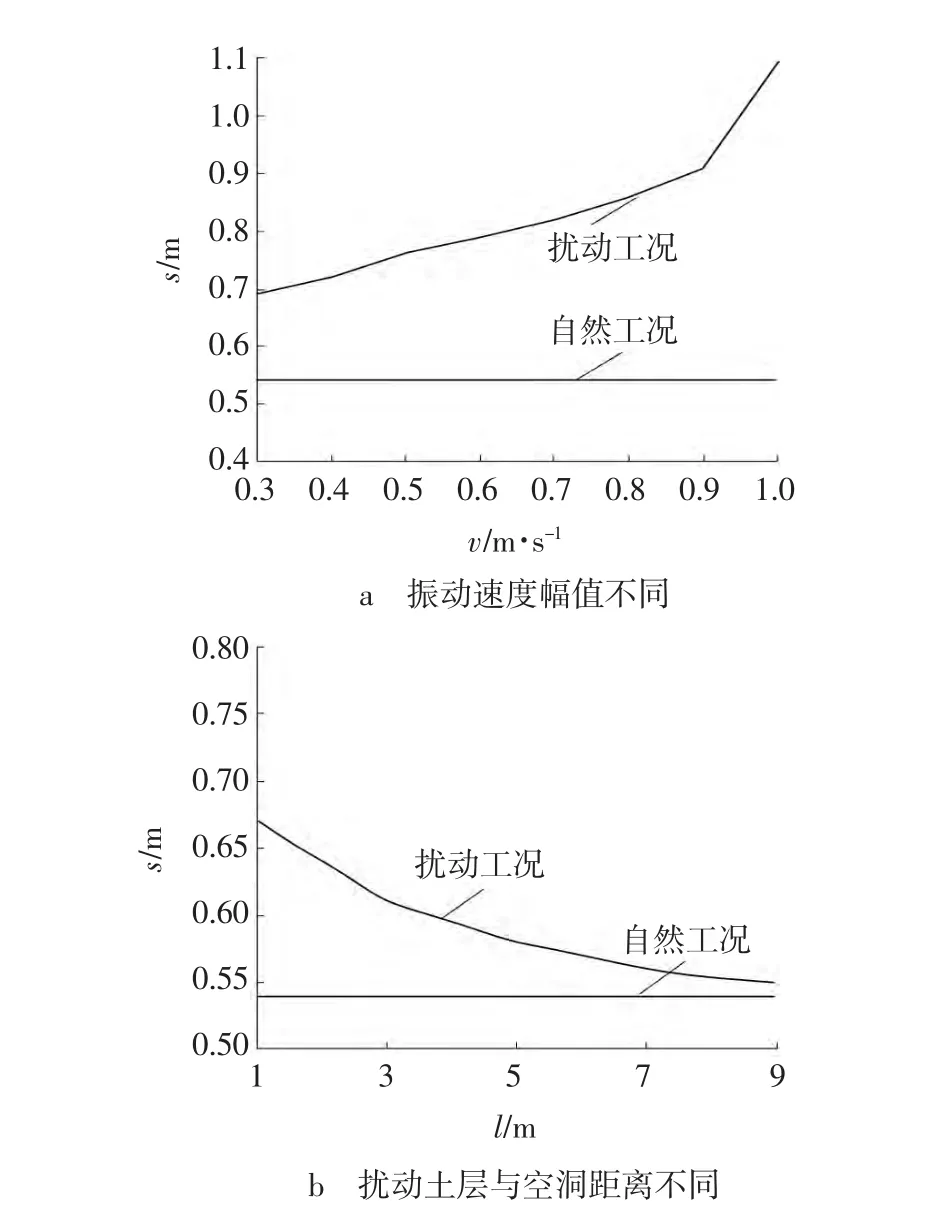
图7 施工扰动与面层沉降关系曲线Fig.7 Relationship of construction disturbance and surface subsidence
从图7中可以看出,施工扰动对道路面层的沉降变形有一定的影响。在空洞周围近距离施工时,对面层沉降产生较大影响,扰动越剧烈,空洞坍塌的可能性和程度越大,面层变形也更大;扰动土层与空洞距离和面层沉降值之间的关系曲线较为平缓,根据数值分析的结果,可仅考虑二者相距在3 m以内时,施工扰动对道路安全性的影响。
3.4 路基土性对路面沉降的影响
路基的土性条件对道路的安全性影响很明显,软土可能在自重应力条件下就会产生一定范围内的松动区、脱空区。文中采用直径2 m、埋深2 m的空洞数值模型,考虑土层的黏聚力和摩擦角两个因素,进行土性影响分析,以反映地下空洞处于不同土层时路面沉降变化规律。图8给出了不同黏聚力和摩擦角情况下的道路面层沉降曲线。
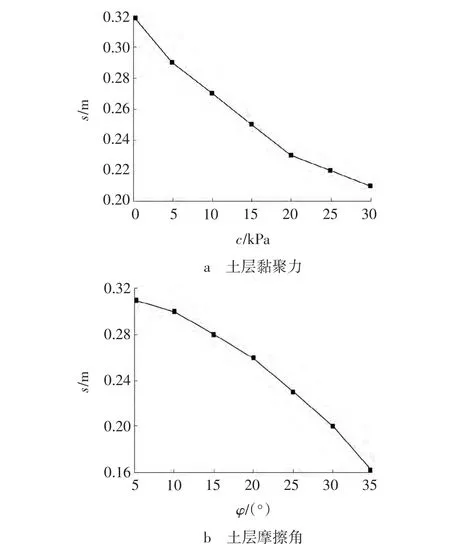
图8 土性条件与面层沉降关系曲线Fig.8 Surface subsidence curves under properties of soil
从图8中可以看出,随着土层黏聚力和摩擦角的增加,道路面层的沉降值均单调递减,对结构安全性的影响比较明显。然而,黏聚力与沉降值的关系曲线是“内凹型”,即随着黏聚力的增加,面层沉降变形有放缓的趋势;而摩擦角与沉降值的关系曲线是“外凸型”,即随着土层摩擦角的增加,面层沉降变形的减小有加快的趋势。
4 结论
结合工程实例,基于PFC2D软件模拟地下空洞发展的演变过程及其对道路路面沉降的影响效果,可得到如下结论:
(1)道路路面沉降随着空洞埋深的减小和尺寸的增大,均出现先急剧增加后趋于平缓的过程,该曲线的拐点为道路安全性预测的关键点,对实例中特定土层,其关键点为直径6 m、埋深6 m。
(2)施工扰动会显著影响下伏空洞的道路路面沉降,当空洞与扰动土层相距3 m以内时,必须考虑施工扰动的影响。
(3)路基土性对路面沉降影响效果显著,沉降值随空洞所在土层的黏聚力和摩擦角均近似呈线性变化。
(4)该文从颗粒细观参数角度揭示了地下空洞发展至路面塌陷的破坏机制,为地下病害研究提供了一种新方法。
[1] 宋谷长,叶远春,刘庆仁.北京市城市道路塌陷成因及对策分析[J].城市道桥与防洪,2011(8):250-252.
[2] 李智强.城市道路塌陷成因与机理分析[J].华东公路,2013(4):3-5.
[3] 高明生.城市道路塌陷原因分析及预防措施[J].市政技术,2014(S1):39-42.
[4] 陈昌彦,肖敏,贾辉,等.城市道路地下病害成因及基于综合探测的工程分类探讨[J].测绘通报,2013(S2):5-9
[5] 雷六斤.城市道路塌陷的成因及隐患探查[J].测绘通报,2013(S2):254-255.
[6] 余乐.城市地层不同形态空洞失稳破坏机制的试验研究[D].北京:北京交通大学,2013.
[7] 翟淑花,郑建春,邢涛.地下空洞演化对既有地下管线的影响分析[J].给水排水,2012(S1):436-438.
[8] 刘红,刘军.离散元法中三种球形颗粒接触发现算法的比较[J].黑龙江科技学院学报,2006,16(6):360-363.
[9] ITASCA CONSULTING GROUP INC.Particle flow code in 2 dimensions,PFC2D version 3.0[M].Minneapolis:Itasca Consulting Group Inc,2002.
[10] 周健,池毓蔚,池永,等.砂土双轴试验的颗粒流模拟[J].岩土工程学报,2000,22(6):701-704.
[11] 刘洋.砂土液化破坏的细观力学机制与数值模拟[D].上海:同济大学,2006.
