基于泄露积分型回声状态网的居民消费价格指数预测

伦淑娴 ，林 健

（1.渤海大学 新能源学院，辽宁 锦州 121013；2.渤海大学 工学院，辽宁 锦州 121013）

居民消费价格指数（Consumer Price Index,CPI）,是一个反映居民家庭一般所购买的消费商品和服务价格水平变动情况的宏观经济指标。它是度量一组代表性消费商品及服务项目的价格水平随时间而变动的相对数，用来反映居民家庭购买消费商品及服务价格水平变动情况[1]。CPI通常被作为观察经济运行水平的重要指标。当指数上升幅度过大时，表明通货膨胀过度，物价上涨，失业率上升，带来经济不稳定。当指数出现负增长时，则表明经济进入通货紧缩状态，造成经济衰退低迷。一般来说，CPI的高低直接影响着国家的宏观经济调控措施的出台与力度，如央行是否调息，是否调整存款准备金率等。同时，CPI的高低也直接影响资本市场的变化。在众多经济指标中，CPI是一个广受关注的重要的经济指标。

文中采用泄漏积分型回声状态网（Leaky Integrated Echo State Network,Leaky ESN）模型对2013-2014年各月的CPI进行预测，通过对比CPI的实际值，证明该方法的有效性。此外，将Leaky ESN的预测误差与ARIMA模型作对比，证明Leaky ESN具有更高的预测性能。

1 差分自回归移动平均模型

差分自回归移动平均 （Auto-regressive Integrated Moving Average,ARIMA）模型是由Box和Jenkins于70年代初提出的一种著名的时间序列预测方法[2]。其中ARIMA（p,q,d）称为差分自回归移动平均模型。它是从时间序列本身的特点出发，建立相应的模型进行分析，得出其过去行为的相关结论，并对其未来的行为进行预测和推断。用这种方法预测时，不必考虑其他因素对其产生的影响，这样避免了寻找影响因素的困难。ARIMA模型理论分析深入彻底，应用分析简单、有效，因此成为线性时间序列预测的主要工具。

近年来，许多学者利用ARIMA模型进行了人口、水文、交通、能源需求量等方面的预测[3-5]。

1.1 ARIMA的建模原理

ARIMA （p,d,q）模型中的AR代表自回归，I代表综合运算，MA代表移动平均。其中的参数p为自回归项，d为时间序列达到平稳时所做的差分次数，q为移动平均项数。所谓的ARIMA模型，是指将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值，以及随机误差项的当前值和滞后值进行回归所建立的模型。ARIMA模型的基本思想是：将预测对象随时间推移的形成的数据序列看作一个随机序列，用一定的数学模型来近似描述这个序列。这个模型一旦被识别以后就可以从时间序列的过去值及当前值预测未来值。这样可以从本质上认识时间序列的结构特征，从而实现最小均方误差意义下的最优预测。

Yt是时间序列在t时刻的观察值，也称为因变量；Yt-1，Yt-2，…，Yt-p是时间序列在 t-1，t-2，…，t-p时刻的观察值，也称为自变量；εt是一个白噪声过程；c，Φ1，Φ2,…，Φp，θ1，θ2，…θq未知参数。

1.2 ARIMA建模步骤

1)根据时间序列的散点图、自相关函数和偏自相关函数以ADF单位根检验其方差、趋势及其季节性变化规律，对序列的平稳性进行识别。如果ADF检验值大于单位根检验的临界值，则认定该时间序列为非平稳时间序列。一般来讲，经济运行的时间序列都不是平稳序列。

2)对非平稳序列进行平稳化处理。若数据序列是非平稳的，并存在一定的增长或下降趋势，则需要对数据进行差分处理。若数据存在异方差，则需要对数据进行差分处理，直到处理后的数据的自相关函数值和偏相关函数值无显著地异于零。通过这一步，可以确定p,d,q的值。

3)根据时间序列模型的识别规则，建立相应的模型。模型的选择标准如表1所示。

4)模型诊断和检验。模型诊断与检验有两种方法：一是根据模型的残差序列是否为白噪声序列来判断模型是否为适应性模型；二是通过计算ARIMA（p,d,q）模型的特征根来检验其平衡性。

表1 ARIMA识别原则Tab.1 ARIMA recognition princip le

5)预测和评价。运用确定的ARIMA（p,d,q）模型对数据进行预测。首先预测序列末尾的数据，与原始序列对比得出预测误差，若预测误差较小，则可运用该模型对未来的数据进行预测。

2 泄露积分型回声状态网

泄漏积分型回声状态网 （Leaky Integrated Echo State Network,Leaky ESN）是回声状态网（Echo State Network,ESN）的一种改进模型[6]，其储备池是由泄露积分型神经元组成。这种类型神经元具有独立的状态动力学信息，可以利用各种方式来适应网络学习任务的时序特征。Leaky ESN与ESN的拓扑结构相同，如图1所示[7]。图1中左侧为K个输入节点；中间是储备池网络，由N个内部节点以及稀疏的节点连接权值构成；右侧是L个输出节点。图1中实线表示了网络的必要连接，而虚线表示了不同情况下可能存在的连接，但它们对于构成ESN并不是必需的。Leaky ESN修正了ESN的储备池内部神经元状态更新方程。

图1中输入层输入单元为u(k)，储备池的神经状态为x(k)，输出层输出单元为y(k)。

Leaky ESN网络的状态更新方程为：

其中，f(·)表示神经元激活函数。u(k+1)表示系统在k+1时刻的输入单元，x(k)表示储备池状态向量在k时刻的取值,y(k)表示系统在k时刻的输出单元。Win、W、Wback分别表示输入、储备池和反馈连接权矩阵。a是泄漏率，γ是伸缩参数。

图1 Leaky ESN的网络拓扑结构Fig.1 The topology of the Leaky ESN

由（1）式可以看出，ESN 是 Leaky ESN 在 γ=1，a=1 时的特例。通常只要参数选择合适，Leaky ESN的储备池性能优于基本ESN。

ESN的输出方程为：

式中 fout(·)表示输出函数，根据问题的不同 fout(·)可以取线性函数或者S型函数，Wout表示输出连接权矩阵，需要通过在线或者离线的算法训练得到。

Leaky ESN的数学模型可以看作是作用在储备池状态神经元上的低通滤波器。泄漏率a控制前一时刻神经元状态的保持程度，其截止频率由参数a决定。较小的a取值导致内部神经元状态x(k)的较慢变化，从而明显增强了ESN的短时记忆能力。特别值得一提的是，Leaky ESN在训练阶段只改变输出连接权值，而其他权值固定不变。

3 两种模型的CPI预测效果比较

为了证明文中所提出的Leaky ESN的可行性和实际应用价值，对2013—2014年各月的CPI进行预测，并且与ARIMA模型的预测数据作对比，分析两种模型的预测效果。

文中的数据来源于国家统计局数据库，所选取的CPI为同比消费价格指数，即假设上年同月的CPI为100，按照增减比例得出本月当前值，2013-2014年各月的CPI具体数据如表2所示。

由于ARIMA模型的优点在于不仅考察了预测变量的过去值，而且对模型的过去值拟合产生的误差也作为重要因素纳入模型。此外，利用ARIMA模型时不需要预先确定序列的发展形态，通过先假设一个可能的形式，通过反复的模型识别和修正，最终得到最佳的拟合方程来进行预测。因此，ARIMA在非平稳时间序列预测方面具有一定的优势。

表2 2013～2014年同比消费价格指数实际值Tab.2 The actual value of year-on-year CPI from 2013 to 2014

Leaky ESN是通过改变传统ESN中的储备池内部神经元类型达到优化目的，是当前最普遍的改进ESN的一种方式。它不仅解决了传统ANN训练复杂、收敛速度慢、容易陷入局部极小等问题，而且其储备池相对传统ESN来说，存储记忆功能更强，从而具有更高的预测精度。用Leaky ESN模型预测CPI，选取1987～2014年336个月的CPI作为样本，前半部分数据用来训练，后半部分数据用来预测。为了消除系统偶然性，训练过程中遗忘48个数据，从剩余的预测数据中选取2013～2014年的24个数据作为对照样本，研究该方法的预测性能，具体数据如表3所示。

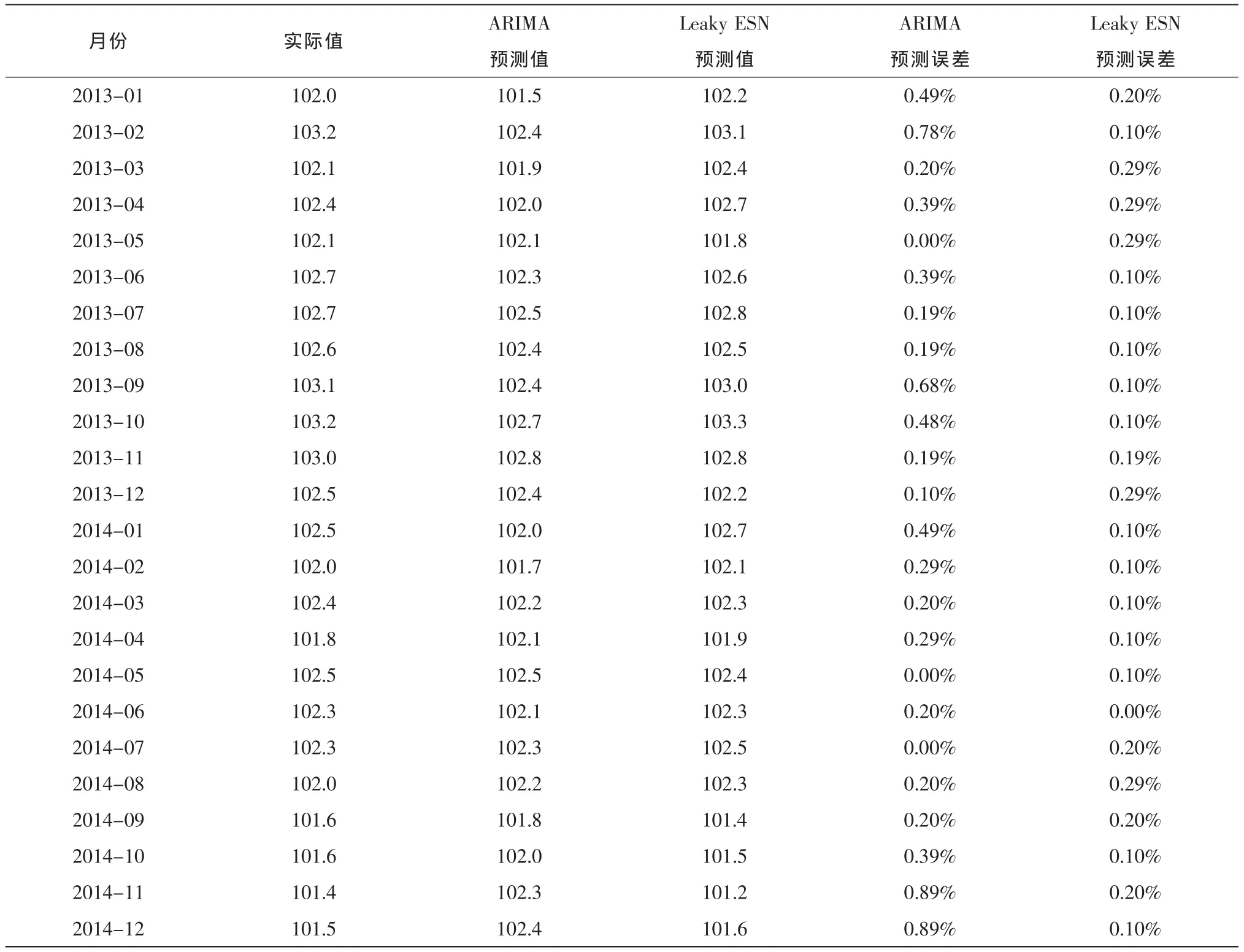
表3 2013～2014年居民消费价格指数预测值和实际值Tab.3 The predictive value and actual value of the CPI from 2013 to 2014

为了直观的观察这两种方法的预测结果，将各月的实际值和预测值对应的数据放在同一张图中，用MATLAB软件作出相应的折线图，如图2所示。

图2 两种方法的预测值与实际值的对比图Fig.2 The comparison of predictive value and actual value of twomethods

通过图2可以看出，这两种方法都能大致预测CPI各月的数据，基本接近实际值。为了对比这两种方法的预测精度，将各自的测量值与实际值对应作差，如图3所示。

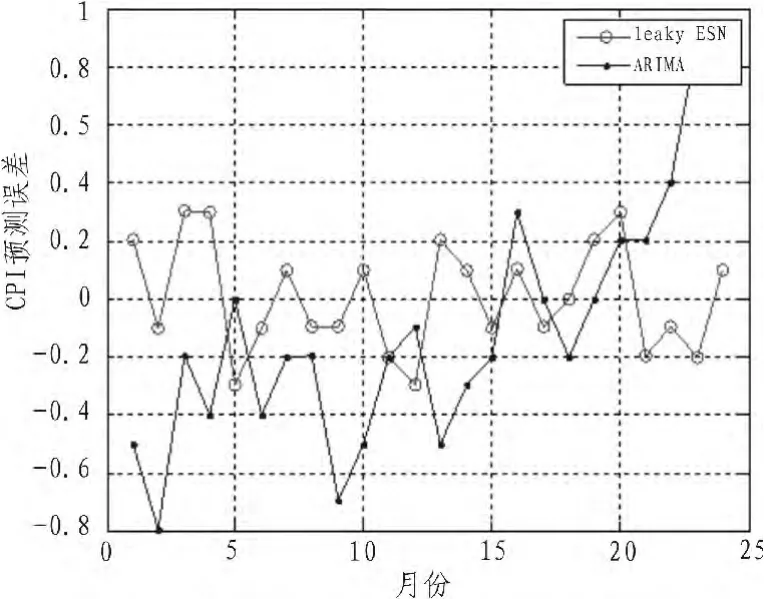
图3 两种方法的预测误差对比图Fig.3 The comparison of predictive error of twomethods

从图3可以看出，ARIMA模型的误差收敛性最差，误差随着时间的延长先波动减小，最后迅速增大。因此，ARIMA模型只适用于短期数据预测。Leaky ESN的误差在零附近较小的范围内上下波动。为了更加明确的比较这两种方法的预测性能，对表3中的数据进行统计分析，分析结果如表4所示。

表4 两种方法预测误差对比Tab.4 The comparison of predictive error of two methods

对比表4中的数据可知，Leaky ESN模型的两种预测误差都远远小于ARIMA模型。Leaky ESN相对于ARIMA模型来说，在CPI预测方面具有较大的优势。

4 结论

当前，ARIMA模型是CPI预测中应用最普遍的方法，采用差分的方法将非平稳时间序列转化为平稳时间序列，在短期预测中能够取得较好的效果。但是，为了更好的掌控消费价格状况，为各种政策的制定提供可靠的依据，需要对CPI进行长期预测。因此，本文提出了Leaky ESN模型，Leaky ESN是一种新型的递归神经网络，具有良好的自学习能力和非线性逼近能力。通过实验对比，Leaky ESN的平均相对误差相对ARIMA模型减小了52.9%，均方根误差减小了58.1%，证明Leaky ESN具有更好的预测效果。

[1]何书元.应用时间序列分析[M].北京:北京大学出版社，2003.

[2]Box G,Jenkins G,Time Series Analysis Forecasting and Control[M].San Francisco:Holden Day Press,1970.

[3]俞金国，王丽华.后SARS时期中国入境旅游人数恢复评估—基于ARIMA模型[J].统计与决策，2005（7）：84-86.

[4]Contreras J.ARIMA models to predict next-day electricity prices power systems[J].IEEE Transactions,2003,(3):1014-1020.

[5]张杰，刘小明，贺玉龙，等.ARIMA模型在交通事故预测中的应用[J].北京工业大学学报,2004(4):1295-1299.

[6]Herbert Jaeger,Mantas Lukoˇseviˇcius,Dan Popovici.Optimization and applications of echo state networks with leaky integrator neurons[J].Neural Networks,2007(3):335-352.