基于MMC技术柔性直流输电系统调制策略选择方法
2015-03-16彭冠炎
彭冠炎
(中国能源建设集团广东省电力设计研究院有限公司,广东广州510633)
基于MMC技术柔性直流输电系统调制策略选择方法
彭冠炎
(中国能源建设集团广东省电力设计研究院有限公司,广东广州510633)
本文针对模块化多电平拓扑结构换流器,基于PSCAD-EMTDC建立谐波仿真计算模型,研究最近电平逼近与载波移相两种不同调制策略下电平数与谐波含量之间的关系,为换流器选择合适的调制策略提供重要技术支撑。
柔性直流输电;模块化多电平;谐波;调制策略;电平数
模块化多电平 (Modular multilevel converter MMC)是目前发展迅猛的一种换流器拓扑结构,同一拓扑结构的不同调制方式对输电系统的经济性、可靠性、暂稳态特性等均有很大的不同,直接影响工程实际的造价与性能,针对目前主流MMC换流器拓扑结构,研究合适的调制策略意义重大。
柔性直流输电系统由于运行状况的非线性,换流器在其运行时会产生谐波,最近电平逼近 (Nearest level modulation,NLM)与载波移相 (Carrier Phase Shift Modulation,CPSM)2种不同调制策略在电平数一定的情况下谐波的含量各不相同,鉴于谐波的危害性〔1-3〕,文中结合谐波特性及含量、开关损耗、可靠性等因素对2种不同调制策略仿真得到的结果进行分析比较研究,为MMC拓扑结构换流器选择合适的调制策略给出建议。
1 MMC拓扑换流器结构和原理
模块化构成的三相MMC换流器结构如图1所示,图1(a)为MMC换流器的基本单元,是一个半桥换流单元;图1(b)为多组变流单元级联在一起构成一个换流桥臂;图1(c)为6组级联换流桥臂组合在一起构成三相换流器〔4-6〕。
MMC变流器的每个换流单元输出将具有0和Vc两种状态,如果每个桥臂有N个换流单元,则桥臂输出电压的状态将在0,Vc,2Vc,…,NVc之间变化,即具有N+1个电平状态。

图1 MMC换流器结构图
2 NLM方法的谐波解析
NLM方法类似一种波形拟合的方法,使换流器输出台阶波形拟合正弦波形,当电平数目比较大时,输出的台阶波形与正弦波形有较好的拟合度,也具有较小的谐波〔7-8〕。
NLM方法的典型波形如图2所示,可以采用傅立叶级数的方式进行解析分析,第n次谐波的电压可以表示如下:
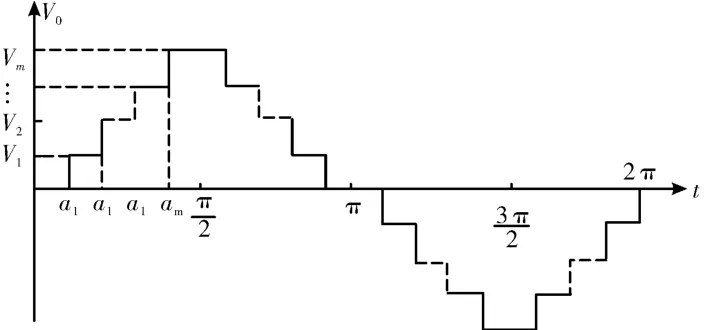
图2 NLM方法波形示意图

如果得到各电平所对应的阶跃角度αk,即可对NLM方法的谐波进行解析计算〔7-8〕。
由于NLM方法依据参考正弦波 (归一化后)取其最为接近的电平数目,当电平数目为奇数时电平阶跃变化处为参考波等于2个电平的中间点

式中 k=1,2,…,N/2。
当电平数为偶数时,与奇数电平的主要区别是不会有中间电平 (或者说0电平),并且:

式中 n=1,2,…,(N-2)/2。
3 CPSM方法的谐波解析
载波移相调制属于脉冲宽度调制 (Pulse Width Modulation,PWM)方法在多电平领域中的应用,通过参考波与一组三角载波的比较得到脉冲控制信号。当这组三角波之间相位相互错开时,称为载波移相调制方法〔9-10〕。
对于一个N电平逆变器,可以采用K1个载波频率为ωc1,调制比为M,载波相位角度依次错开角度δ=2π/K1的两电平PWM,实现N=K1+1电平PWM方法,最后的PWM电压是这些两电平PWM电压的和,每个两电平PWM相电压为:
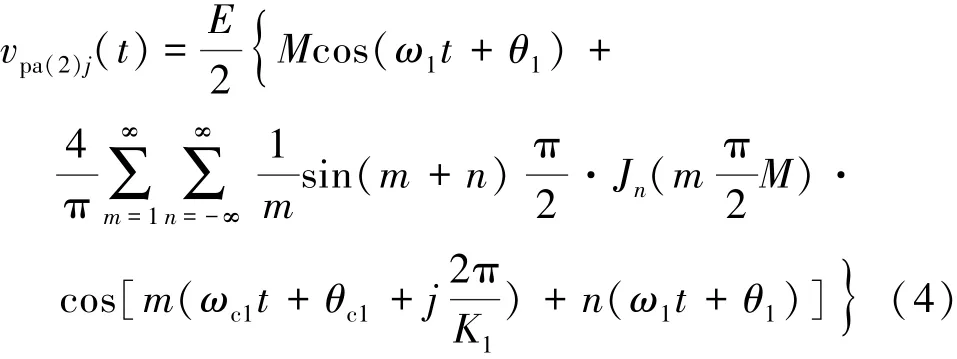
式中 j=1,2,…, K1。显然如下关系成立

式中 k=1, 2, 3, …, ∞ 。
这样,总的二电平载波移相PWM电压可以写成
K将K1E/2= (N-1)E/2=Edc/2代入到式 (6)中,并仍用m表示载波倍数,则式 (6)为:
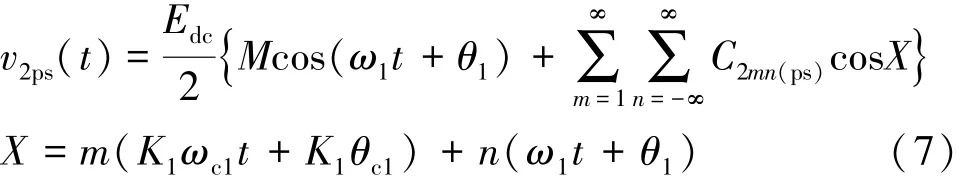
其中谐波幅值系数可以写成

式 (7)就是载波移相PWM策略的谐波分布表达式,这与两电平PWM谐波表达式十分相似。从分析过程可以看出,由于载波移相作用,原来的两电平PWM电压中,载波倍数m为非K1整数倍的载波频带及其边带谐波,通过载波移相叠加后全部被消除掉。从式 (8)的谐波分布表达式来看,多电平载波移相PWM策略就是相当于将原有的两电平PWM载波频率提高了K1倍,即最后的多电平PWM的等效载波频率为ωc=K1ωc1,谐波也以这个等效的载波频率分布在相应的载波频带及其边带中,类似于两电平PWM的谐波分布规律。
4 NLM与CPSM方法的谐波仿真分析
为了验证上述理论分析结果,基于 PSCAD/ EMTDC建立MMC换流器谐波分析仿真模型,在一定电平数目下,采用不同的调制策略对比分析两种调制策略的优缺点,仿真模型参数见表1。为了方便,设定相同的工作条件,仿真模型使用了逆变侧单端换流器,直流侧直接用±150 kV的直流电压源代替,交流输侧直接连接PQ负荷模型。逆变站带无源负载的模型便于直接设定调制比等运行参数,也便于与理论计算值的直接比较。

表1 仿真模型参数
总谐波失真 (Total harmonic distortion,THD)在幅值方面反映了谐波畸变程度,(Harmonic current factor,HCF)指标更多的反映了换流器谐波引起的注入电网中谐波电流的特性,电话谐波波形系数(Telephonic harmonic form factor,THFF)评价母线电话谐波对邻近通信线路影响的关键指标。图3为THD与调制策略、电平数目的关系曲线图,图4为HCF与调制策略、电平数目的关系曲线图,图5为THFF与调制策略、电平数目的关系曲线图。
仿真结果结合理论分析:

图3 THD随电平数变化

图4 HCF随电平数变化

图5 THFF随电平数变化
NLM方法是一种通过电平数目的叠加拟合正弦参考波的方法,电平数越少正弦波的拟合程度越差。载波移相是一种将开关的频率提高到 K1倍(K1=N-1),所以CPSM等效的开关频率比NLM更高。单次谐波畸变Dn=Un/U1×100%(其中U1是系统基波相电压有效值,Un为n次谐波相对地电压有效值)总谐波畸变率为:

式 (9)中,N表示所考虑的最高谐波次数,开关频率越高,THD就越高。同时仿真结果说明在电平数目在一定程度时,电平数目N的提高对THD的降低效果比开关频率的增加更好。
1)当N在100以内时,CPSM方法的HCF指标和THFF指标都小于NLM方法。当N大于100时候,CPSM和NLM方法的HCF指标和THFF指标差别不大。

式中 n表示n次谐波分量;NH为最高谐波次数;Fn=pnnf0/800; pn为听力加权系数; f0为基波频率。
由于CPSM的开关频率比NLM更高,开关频率的提高将谐波的次数提高,从而对谐波次数敏感的HCF和THFF指标降低。在电平数达到一定程度的时候两者的计算结果几乎一致。
2)随着N增大,开始阶段THD的降低非常明显,但是当N>90以后,各项指标的下降速度明显减缓,实际上这时再增加电平数目已无明显改善效果。
NLM方法随着电平的增加拟合的正弦波与真实的波形约接近,这种情况下输出波形将非常接近正弦波,各次谐波含量和THD都将比较小;CPSM提高开关的频率也大大降低THD。然而NLM方法开关频率固定为基波频率,因此谐波性能主要受到调制比的影响;CPSM方法则还有开关频率的选择。CPSM方法谐波指标受载波比变化的影响,当载波比达到一定程度再继续增加载波比。对于改善谐波指标的作用也不再明显,同时增加载波比,提高开关平率比会带来开关过大的损耗。对于改善谐波性能来说,提高电平数目比提高开关频率更有效果,但是当N>90时再继续提高电平数目对改善谐波等性能指标已无明显意义。
3)NLM和CPSM调制策略适应的电平数存在分界点,综合改善谐波含量与降低模块的损耗进行评价,在电平数分界点以下采用载波移相调制策略比最近电平逼近更优,反之则否。
在每根骨架上划出“十”字定位线,实际测量后,将数据与三维模型数据进行对比并对数据进行修正。最后,减去玻璃之间的离缝得出最终的玻璃尺寸。汇总玻璃数据信息提交专业生产厂家生产。
5 仿真结果与理论计算对比
考虑短路电流的影响,在没有设置滤波器的情况下NLM方法和CPSM的THD理论计算结果如图6和图7所示。
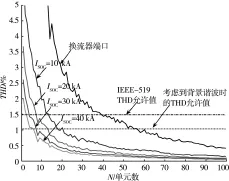
图6 NLM方法THD随电平数目的变化曲线
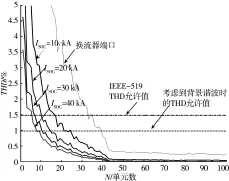
图7 CPSM方法THD随电平数目的变化曲线
通过对比图6,图7和图3,理论计算及仿真的结果接近,证明了仿真模型及仿真结果的正确性,同时证明了NLM方法在原理上是适用于电平数目比较高的情况下,可以较好的与正弦电压实现拟合,并得到较好的谐波性能。在电平数目比较低的情况下NLM方法则并不适用,应该采用提高开关频率的手段来保证谐波性能,采用CPSM方法。
6 结语
文中分别针对NLM调制方法和载波移相调制方法,建立了MMC换流器交流侧谐波特性的分析计算方法;给出了采用不同调制策略时的谐波分布特性,给出了谐波随频率次数的变化关系。分析了交流侧谐波特性随主要电路参数和调制参数的变化规律,例如级联单元数目、调制策略和载波比等主要参数,为MMC换流站的主回路参数设计和调制策略选择提供重要的依据。
〔1〕汤广福.基于电压源换流器的高压直流输电技术〔M〕.北京:中国电力出版社,2010.
〔2〕Franquelo L G,Rodriguez J,Leon J I,et al.The age of multi-level converters arrives〔J〕.IEEE Industrial Electronics Magazine,2008,2(2):28-39.
〔3〕赵畹君.高压直流输电工程技术 (第2版)〔M〕.北京:中国电力出版社,2011.
〔4〕刘钟淇,宋强,刘文华.基于模块化多电平变流器的轻型直流输电系统〔J〕.电力系统自动化,2010,34(2):53-58.
〔5〕Hagiwara M,Akagi H.PWM control and experiment of modular multilevel converters〔C〕 //IEEE Power Electronics Specialists Conference.Rhodes,Greece:IEEE,2008:154-162.
〔6〕丁冠军,汤广福,丁明,等.新型多电平电压源换流器模块的拓扑机制与调制策略〔J〕.中国电机工程学报,2009,29 (36):1-8.
〔7〕管敏渊,徐政,潘伟勇,等.最近电平逼近调制的基波谐波特性解析计算〔J〕.高电压技术,2010,36(5):1 327-1332.
〔8〕 Hagiwara M,Akagi H.Control and experiment of pulsewidthmodulated modular multilevel converters〔J〕.IEEE Trans on Power Electronics,2009,24(7):1 737-1 746.
〔9〕赵昕,赵成勇,李广凯,等.采用载波移相技术的模块化多电平换流器电容电压平衡控制〔J〕.中国电机工程学报,2011,31(21):48-55.
〔10〕 Allebrod S,Hamerski R,Marquardt R.New transformerless,scalable modular multilevel converters for HVDC-Transmission〔C〕 //IEEE Power Electronics Specialists Conference.Rhodes,Greece:IEEE,2008:174-179.
Selection of modulation schemes of flexible DC transmission system based on MMC
PENG Guanyan
(China Energy Engineering Group Co.Ltd,Guangdong Electric Power Design Institute,Guangzhou 510663,China)
This paper establishes the harmonic simulation model based on PSCAD-EMTDC,researches the nearest level and carrier phase shift modulation strategies for the modular multilevel converter topology structure,and gets the relationshi between level numbers and harmonic contents.The research conclusion provides important technical support of selecting a suitable modulation scheme for converters.
flexible DC transmission;modular multilevel converter(MMC);harmonic;modulation schemes;the number of level
TM721.1;TM464
A
1008-0198(2015)06-0006-04
10.3969/j.issn.1008-0198.2015.06.002
彭冠炎 (1984),男,硕士研究生,工程师,研究方向为柔性直流输电技术。
2015-03-02 改回日期:2015-06-12
国家863研究项目:大型风电场柔性直流输入接入技术研究与开发示范工程中能建广东电力设计研究院科技项目 (WC0049E1)
