基于可靠性评估的配电系统长期检修策略研究

路建明，危瑾，陈远扬

(1.国网湖南省电力公司，湖南 长沙 410007；2.国网湖南省电力公司长沙供电分公司，湖南 长沙 410015)

基于可靠性评估的配电系统长期检修策略研究

Long-term maintenance scheduling of distribution system based on reliability estimation

路建明1，危瑾2，陈远扬1

(1.国网湖南省电力公司，湖南 长沙 410007；2.国网湖南省电力公司长沙供电分公司，湖南 长沙 410015)

本文从设备老化特性入手，从系统角度建立了配电系统长期检修优化模型。算例结果表明，该检修模型可有效降低系统失负荷风险、提高系统的可靠性水平和经济性水平。

配电系统；系统可靠性；经济性；检修规划

相比输电系统而言，配电系统中设备类型更多且网络结构复杂，影响运行的因素很多，且直接与电力用户相连，因此其安全稳定运行直接关系着电力用户的用电可靠性〔1－2〕。合理的检修计划不仅可以提高检修的效率，而且可以延长设备寿命，减少其故障概率及停电时间，提高系统可靠性以及系统收益〔3〕。

目前国内配电系统的检修方式主要为定期检修模式，检修时间间隔和检修内容主要根据设备制造商或专家的经验进行确定，容易造成检修过剩或不足。随着电力行业的市场化改革以及配电系统网络的发展与升级、配电系统自动化设备的增加以及用户对用电可靠性要求的增高，定期检修方式越来越不适应电网的发展，迫切需要形成新的检修模式，以提高检修的效率和针对性。

随着电力行业检修理论和水平不断提高，对发输电系统检修的研究已经形成体系，但是作为电力系统中最复杂的网络，目前关于配电系统检修的理论则相对较少。基于此，文中针对配电系统的特点，分析了配电设备的老化过程，并基于设备时变故障率给出了合理制定长期检修计划的模型，以达到系统经济性和可靠性综合效益最佳为目的，并使用实际算例进行了验证。

1 配电系统的检修特性

配电网络结构复杂，运行中的不确定因素很多，因此是电力系统中的一个薄弱环节。对配电设备进行合理的检修是提高整个配电系统可靠性的有效措施，但由于配电系统的复杂性，检修工作需要大量的人力和物力资源。由于配电系统直接连接负荷，因此合理的配电系统检修计划需要考虑负荷波动和用户用电可靠性的影响。

1.1 配电系统直接连接电力用户

配电系统作为直接连接电力系统和用户的桥梁，因此配电设备的运行直接影响到用户的用电可靠性；电力用户的多样性要求配电系统有相应的可靠性指标，同时负荷的变化对配电设备的可靠性指标如故障率有着直接的影响。因此，与发、输电系统检修不同，配电系统检修要以检修经济性、系统可靠性和电力用户的用电指标为基础，来制定配电系统检修模型。

1.2 配电设备种类繁多数目庞大

配电设备的型号规格、容量和数目均随着电力负荷的不同而变化，同一类设备由于安装位置和使用情况的不同其故障率等可靠性指标也不尽相同。因此，对于配电系统而言，使用不变的设备故障率来分析系统可靠性是不合理的，其原始参数和特性数据应该通过长期连续的统计才能反映设备的真实规律。

2 配电系统可靠性模型

2.1 配电网系统可靠性基本理论

配电网是一个由众多不同类型的元件组成的复杂网络，实际运行中的不确定因素很多，无论是设备故障停运还是设备检修停运，均会造成系统网架结构和运行方式的改变，引起系统可靠性水平的降低甚至引起系统切负荷风险的提高。因此，在配电系统检修安排过程中要时刻保证系统的可靠性水平在允许的范围内。

目前国内电力系统主要是进行高、中压用户供电可靠性的管理工作，而低压用户供电可靠性仅处于理论研究阶段。而配电系统的可靠性指标是系统检修的基本依据，通过合理的检修安排不仅可以减少由于设备故障造成的系统切负荷风险，同时可避免由于设备检修停运造成的系统可靠性水平下降。因此，配电系统可靠性评估是文中所提检修模型的核心。配电系统检修安排中需要考虑的可靠性指标如下〔4〕:

1)系统平均停电频率指标 (SAIFI):在给定时间内电力用户的平均停电次数，即

2)系统平均停电时间指标 (SAIDI):在给定时间内电力用户经受的平均停电时间，即

3)用户平均停电频率指标 (CAIFI):在给定时间内受停电影响的电力用户经受的平均停电次数，即

4)用户平均停电时间指标 (CAIDI):在给定时间内受停电影响的电力用户经受的平均停电时间，即

5)电量不足期望值 (EENS):在给定时间内由于设备停运造成的系统向用户供电的电量缺额。

配电系统可靠性评估〔5〕就是利用系统拓扑信息和元件可靠性参数，采用解析法或模拟法评估配电系统的各项可靠性指标〔1－3〕。

2.2 配电设备检修的可靠性模型

一般认为电力系统设备投入运行初期，由于工艺缺陷和装配水平的差异等，设备故障率较高但呈下降趋势；随着设备的运行，设备逐渐达到一个稳定期，此时设备故障率基本维持不变或变化很小，是配电网各设备运行的最佳工作时间；而随着运行时间过长，老化、磨损和疲劳等原因将导致设备性能逐渐恶化、故障率迅速增加，此时极易发生设备损坏，从而影响配电网的正常运行、造成较大经济损失。

当前，不同模型用来模拟不同设备的故障率变化情况，如经常用到的各种 Weibull分布〔6－7〕，其中参数的个数差异及取值不同决定了失效曲线形状及变化趋势，对于一般 “2参数”模型不能同时完整地呈现整个设备运行过程中失效曲线。这里采用文献 〔7〕中的 “5参数”Weibull函数建立数学模型，具体如式 (1):

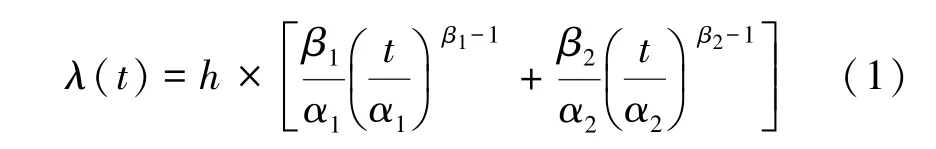
文中基于认为配电设备的故障率是随运行时间的变化而变化的，根据设备的失效原因，如配电线路可能由于植被影响、绝缘子或配套设备损坏以及杆塔损坏等原因而发生故障，认为这些影响设备故障率的因素彼此是独立的，据此将设备故障率分解成相互独立的不同分量k。由于不同分量的故障率是独立的，则设备的故障率对系统的影响可以等效成各分量对系统的影响之和，则文中配电设备故障率如式 (2):

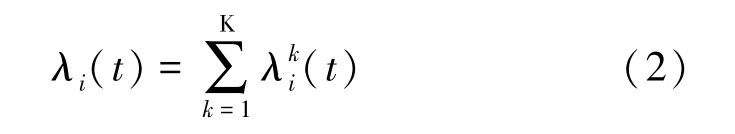
2.3 检修对设备故障率的影响分析

根据电力系统实际检修情况分析，文中认为对不同类型的设备状态采取不同类型的检修，各类型的检修只对其对应的故障率有削减的作用，认为各设备各类型的故障曲线都有一个初始值，经过检修后，故障率会返回到该初始值，并不认为设备经过检修后会返回到全新状态，这更符合设备运行实际情况。对文献 〔8〕中检修对设备故障率的影响公式进行改进，形成本文的检修后设备故障率计算公式如式 (3):

3 配电系统长期检修模型

3.1 目标函数

配电设备检修停运一方面提高了以后时段设备可用度水平，减少了设备发生故障后修复或更换设备的费用，同时改善了系统可靠性水平；另一方面也降低了检修时段的系统可用容量，为维持一定的可靠性水平，甚至需要切除部分负荷，增大了该时段系统的可靠性成本。因此，文中建立以规划周期内的总成本最小为目标函数的检修模型:

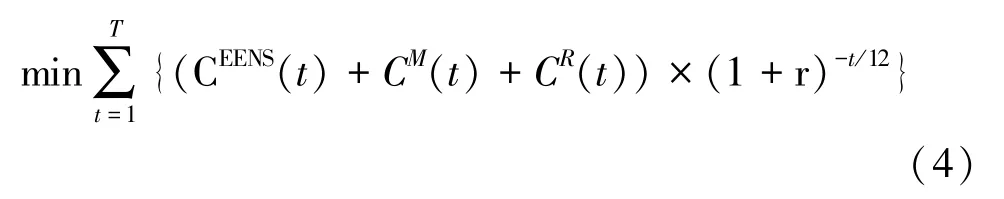
配电设备检修停运与故障停运均会导致系统有一定的失负荷电量，造成相应经济损失，这部分也可以视为系统的可靠性成本。

3.2 约束条件

3.2.1 检修策略约束

配电系统检修策略约束主要考虑检修策略安排过程中的组合问题，常见约束有检修时间约束、检修区间约束、连续检修约束、检修人力约束和检修费用约束等。由于本检修模型考虑的是长期检修安排，检修时段一般以年或月为单位，而配电设备的检修持续时间一般为几个小时，因此本检修模型中检修时间约束、连续检修约束不需要考虑。

3.2.2 系统运行约束

在检修周期内，不同的设备检修决策形成的系统结构、潮流方式也不同。检修安排需要考虑系统运行情况，满足潮流约束、可靠性要求和系统运行约束等，约束条件较为复杂，非线性、离散且随机，需要分析系统运行条件才能验证。

1.配送线路的选择无序。嘉兴A配送中心的产品主要是家电产品，其销售具有非常明显的季节性特点，进入销售旺季时公司的物流配送就没有了系统的调配与管理，中心站点既缺乏了合理的路线选择，也没有了合理的时间安排，出现了物流配送路线选择与车辆搭配的无序性问题。

4 算例分析

4.1 系统参数

文中采用IEEE RBTS母线6系统〔9〕作为算例。算例系统共包括26条线路、13个熔断器、13个配电变压器、13个隔离开关、2个断路器和13个负荷节点，研究周期为5年，即60个月。

由表1可以发现，未检修时系统没有检修成本，即检修成本为0，则系统总成本只由故障后修复成本和可靠性成本组成，其中可靠性成本的比例比较大，达到系统总运行成本的84.96%。

表1 未安排检修时的系统运行成本

4.2 检修结果分析

检修结果显示，文中所提检修模型将大部分设备安排在低负荷时段，而在负荷较高的时段安排检修的设备很少，甚至没有安排设备检修。因此基于文中提出的检修模型所得出的系统检修安排，可避免在高负荷时段进行设备检修带来的失负荷风险，符合系统检修安排的实际情况。检修成本比较见表2。

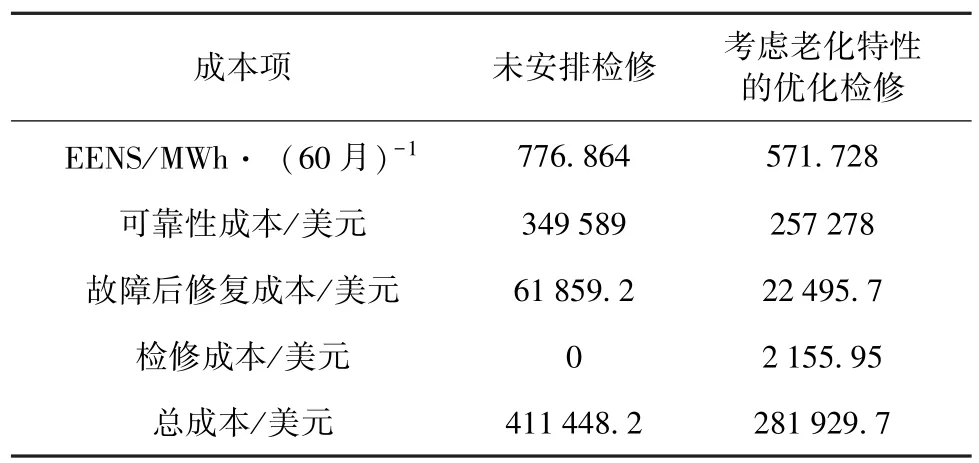
表2 检修安排成本比较

系统优化检修之后，系统在 60个月内总的EENS为 571.728 MWh，比未检修时减少了205.136 MWh；系统在 60个月内总的 SAIFI和SAIDI分别为25.315 7次、147.841 5 h，而未检修时系统的 SAIFI和 SAIDI分别为 11.977 0次、187.408 1 h。由于设备检修会造成负荷短时停电，因此合理的检修安排可能会增加整个检修周期内的停电次数，但可以减少整个周期内的停电时间，并对系统供电不足期望值EENS起到优化的作用。

5 结论

文中首先研究了配电设备的多状态时变故障率模型，然后从系统角度综合考虑系统可靠性和经济性指标，建立了考虑设备老化特性的配电系统长期检修优化模型；利用RBTS系统作为算例系统对检修模型进行分析计算，结果显示本检修模型得出的检修安排符合系统实际情况，优化了系统在规划周期内的运行总成本，使系统经济性指标得到提高，同时大大提高了系统运行的可靠性。

〔1〕王守相，王成山.现代配电系统分析 〔M〕.北京:高等教育出版社，2007.

〔2〕郭永基.电力系统可靠性分析 〔M〕.北京:清华大学出版社，2003.

〔3〕 T.Nakagawa.Maintenance theory of reliability〔M〕.London: Springer，2005.

〔4〕国家电网公司.用户供电可靠性管理工作手册 (第二版)〔M〕.北京:中国电力出版社，2009.

〔5〕别朝红，王秀丽，王锡凡.复杂配电系统的可靠性评估 〔J〕.西安交通大学学报，2000，34(8):9-13.

〔6〕 Xie M，Tang Y，Goh.TN.A modified weibull extension with bathtub－shaped failure rate function〔J〕.Reliability Engineering and System Safety，2002，76:279-285.

〔7〕Feng CY，Wang XF.A competitive mechanism of unit maintenance scheduling in a deregulated environment〔J〕.IEEE Transactions on Power Systems，2010，25(1):351-359.

〔8〕 Jahromi AA，Firuzabad M.F，E.Abbasi.An efficient mixedinteger linear formulation for long-term overhead lines maintenance scheduling in power distribution systems〔J〕.IEEE Transactions on Power Delivery，2009，24(4):2 043-2 053.

〔9〕Billinton R，Jonnavithula S.A test system for teaching overall power system reliability assessment〔J〕.IEEE Transactions on Power Systems，1996，11(4):1 670-1 676.

10.3969/j.issn.1008-0198.2015.04.014

TM732

B

1008-0198(2015)04-0056-04

路建明 (1987)，男，硕士研究生，主要研究方向为电力调度运行。

2015-06-16