协作认知网络中基于用户密度与感知时间的吞吐量优化

崔微微,杜娟,贾晓剑

（1.河南科技学院,河南新乡453003；2.南阳理工学院,河南南阳473000）

协作认知网络中基于用户密度与感知时间的吞吐量优化

崔微微1,杜娟2,贾晓剑1

（1.河南科技学院,河南新乡453003；2.南阳理工学院,河南南阳473000）

在协作认知网络中,增加协作的认知用户数,可以减少本地感知时间,但同时会增加通知时间,所以在优化感知性能时需要权衡考虑认知用户的数量.在考虑通知时间的情况下建立了协作认知网络吞吐量优化模型,在保护主用户的前提下,联合优化用户密度和感知时间使吞吐量最大.仿真结果表明：用户密度较大时,通知时间限制了吞吐量的提高,选择合适的协作用户数才能使吞吐量最优.

认知无线电；协作频谱感知；吞吐量；优化

认知无线电能够对固定分配的频谱实现再利用,解决频谱利用率低的问题,所以近年来受到越来越多的关注.频谱感知是认知无线电的关键技术和实现基础,提高感知性能,使认知用户可以更可靠和有效地利用空闲频谱.协作频谱感知融合了多个认知用户的感知信息,已被证明能够大大提高感知性能[1-7].文献[1]中提出了协作感知来解决隐藏终端问题.文献[2]说明了参与协作的认知用户数越多,感知性能越好.文献[3]中分析了在保护主用户的情况下,如何选择感知周期以使吞吐量最大化.在文献[4]中提出了空间分集的概念来提高集中式认知网络的频谱感知性能.文献[5]提出了一种有效的线性合并模型,将本地感知结果进行线性加权,以提高感知性能.文献[6]说明了协作感知可以减少感知时间,从而提高了数据传输的时间.

在现有的协作感知研究中,建立优化问题时均忽略了认知用户将感知结果传送到融合中心的时间,称为通知时间.实际上随着参与感知的认知用户数的增加,所需的通知时间不断增加,其在周期帧中的比重不断增大,影响感知性能.所以在建立感知模型时,有必要将通知时间考虑在内.本文在周期帧中加入了通知时间,并建立了吞吐量优化的数学模型,目的是在保护主用户的前提下,联合优化用户密度和感知时间,获取最大的吐吞量.

1 系统模型

1.1 WRAN系统

IEEE 802.22工作委员会规定了无线区域网络（WRAN）,使得用户可以机会接入空闲的电视频带[7].图1给出了WRAN的系统拓扑结构图.

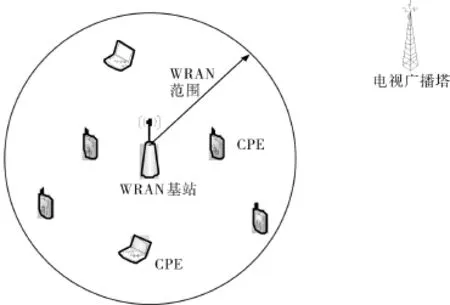
图1 WRAN系统拓扑结构Fig.1 The topological structure of the WRAN system

图1 中,电视广播塔是主用户,WRAN基站是融合中心,WRAN用户终端设备是认知用户.认知用户和主用户相距很远,且认知用户随机分布在以融合中心为圆心的圆周内,假设半径为R,认知用户密度为A,则WRAN系统内的认知用户数为

1.2 协作感知数学模型

在协作认知网络中,每个认知用户首先各自独立地检测授权频带,假设第i个认知用户的接收信号为yi（n）,则其满足以下2种假设

式（2）中假设H0表示主用户存在,H1表示主用户不存在,s（n）是主用户信号,ui（n）是均值为0,方差为σu2的加性高斯白噪声,这里认为s（n）和ui（n）是相互独立的.hi（n）为认知用户和主用户之间的信道增益,|hi（n）|服从瑞利分布.

假设每个认知用户均采用能量检测感知授权频带,则检测统计量为

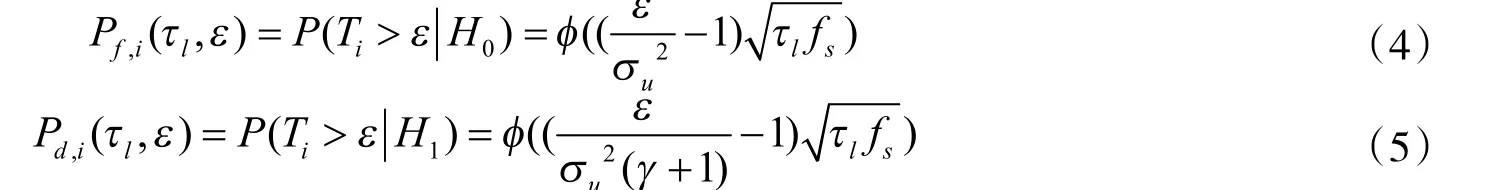
式（4）和（5）中ε为能量检测的判决门限,Φ（·）为正态高斯分布函数.

各认知用户依据检测统计量做出二元决策Di,并将判决结果通过控制信道串行发送到融合中心.设所有的结果传到融合中心所用的时间为,称为通知时间.由于认知用户和融合中心的平均距离为则通知时间为

式（6）中,C为光速.

最后,融合中心采用一定的融合准则将各用户的判决信息融合起来,并给出最终判决.本文采用简单的“或准则”和“与准则”来对检测性能分析优化,同时假设WRAN系统内所有的认知用户都参与了协作感知,则采用“或准则”时,协作感知系统的全局虚警概率和检测概率分别为

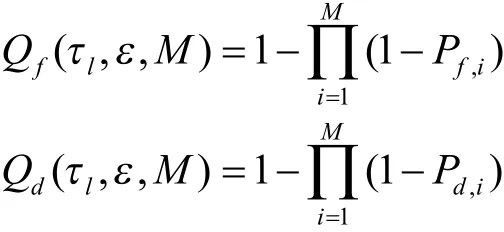
假设所有认知用户的虚警概率和检测概率都是相同的,即Pf,i=Pf,Pd,i=Pd,则

采用“与准则”时,同理可得到

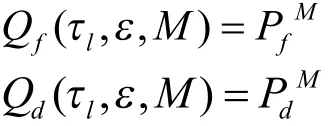
2 协作感知网络吞吐量优化

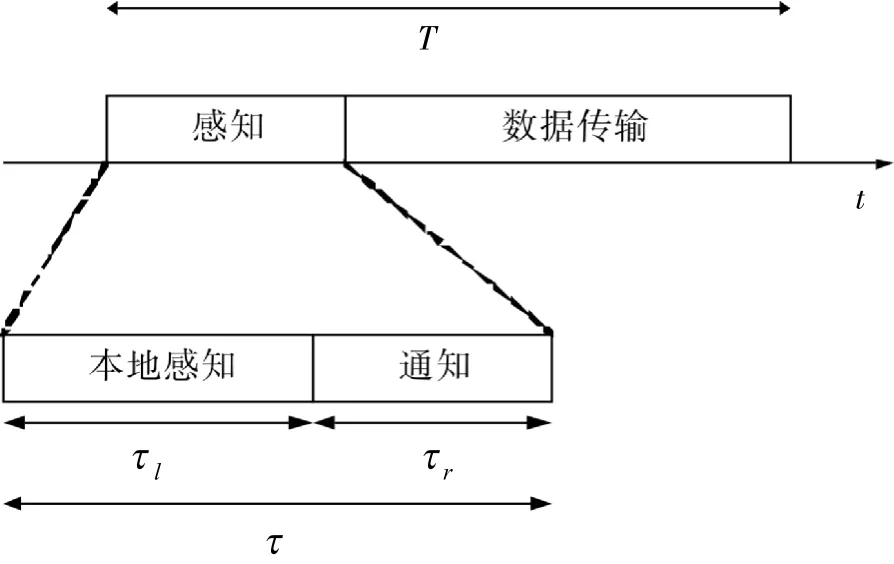
图2 帧结构Fig.2 Frame structure

认知用户只有2种情况可以使用授权频带[3]：

（1）当主用户不存在,且没有虚警概率时,此时的认知用户的平均吞吐量为

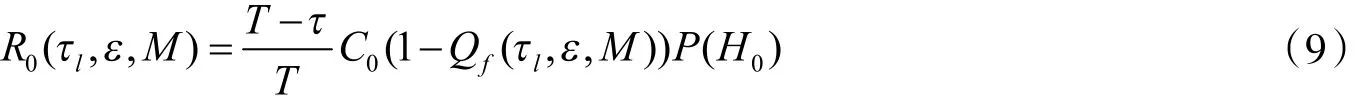
式（9）中,C0表示认知用户在H0下的数据传输速率,P（H0）为主用户不存在的概率.（2）当主用户存在但是没被认知用户检测出来时,认知用户的平均吞吐量为

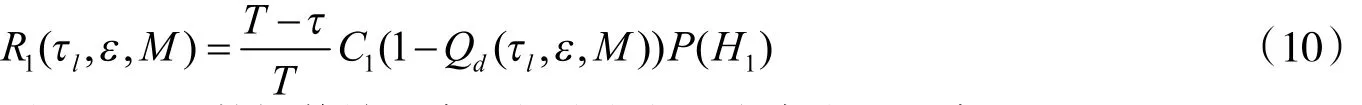
式（10）中,C1表示认知用户在H1下的数据传输速率,P（H1）为主用户存在的概率.则认知网络的平均吞吐量为

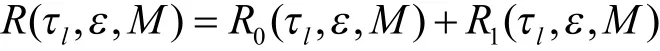
对于主用户而言,要求认知用户在动态接入授权频带时,不能对其产生影响,这就需要检测概率必须足够大,取接近于1的值,则要求.对于认知用户而言,希望在给定时,吞吐量能够最大化.则协作认知网络的优化问题可以描述为

WRAN系统的覆盖半径平均值为33 km,则由式（1）可得,认知用户数只与用户密度A有关,所以式（12）等同于

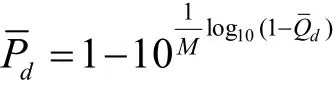
带入式（5）得

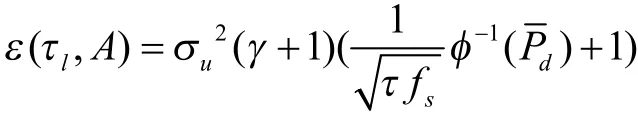
对于“与准则”可以进行类似推导,这里不再详述.则式（13）可简化为

首先证明对于给定的A,即认知用户数M,存在最优的感知时间τ .令可以算出的一阶导数分别为

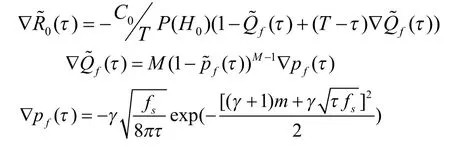
显然,

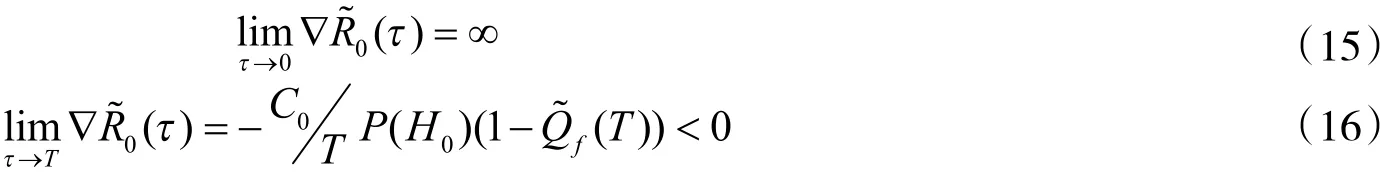
3 仿真与结果分析

利用matlab软件对上述优化问题进行相应的仿真.仿真中的参数设置如下：帧长T=20ms,抽样频率由于主用户和认知用户距离较远,所以信噪比比较低,令γ=-20 dB.

3.1 感知时间和用户密度的关系

图3 本地感知时间和用户密度的关系Fig.3 Relationship between the local sensing time and the user density

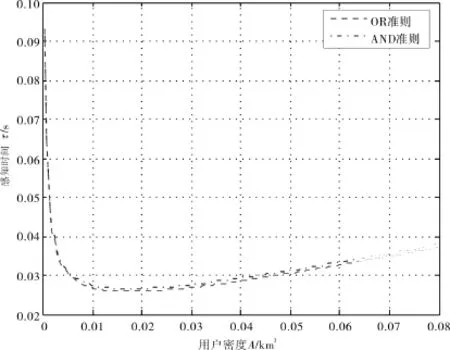
图4 感知时间和用户密度的关系Fig.4 Relationship between the sensing time and the user density

由图3可知,随着用户密度的增加即认知用户数的增加,本地感知时间不断地减小.也就是说多用户进行协作,可以减小达到目标概率所需的感知时间.但当加入通知时间之后,如图4所示,感知时间在用户密度较小时,随着用户密度的增加而减小,但当用户密度增加到一定值后,感知时间开始增加.原因就是用户密度大到一定值后,通知时间增加的值大于本地感知时间减小的值.同时图3和图4中,均仿真了“与准则”和“或准则”2种情况,可以看到2条曲线基本重合,也就是说达到目标概率所需的感知时间不受融合准则的影响.

3.2 吞吐量和感知时间的关系

图5给出了分别采用“与准则“和“或准则”时归一化吞吐量和感知时间的关系.

由图5可知,采用“或准则”时的吞吐量明显优于“与准则”,同时存在一个最优的感知时间使得吞吐量最大化.

3.3 归一化吞吐量和用户密度的关系

图6给出了“或准则”下采用不同信噪比时归一化吞吐量和感知时间的关系.

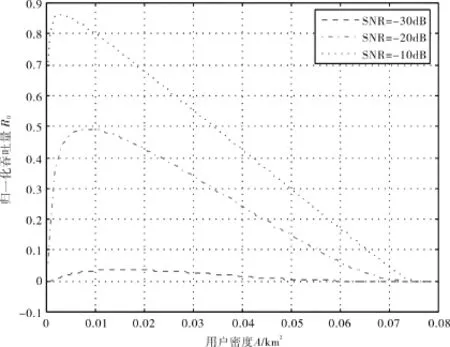
图6 “或准则”下吞吐量和感知时间的关系Fig.6 Relationship between throughput and sensing time under OR fusion rule

由图6可知,存在一个最优的用户密度来使吞吐量最大化,同时,信噪比越高,吞吐量越大.图5和图6说明,需要联合优化感知时间和用户密度使吞吐量最大,同时这个最优值存在.

3.4 不同信噪比下的最优用户密度和感知时间

图7和图8给出了不同信噪比时的最优用户密度和感知时间.

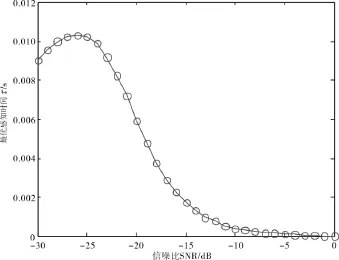
图7 不同信噪比下的最优感知时间Fig.7 The optimal sensing time under different SNR

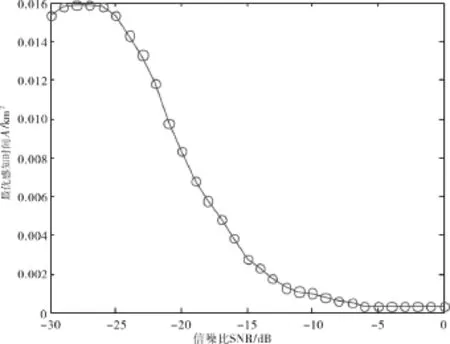
图8不同信噪比下的最优用户密度Fig.8 The optimal user density under different SNR

图7 说明在信噪比极低时,如-30 dB到-24 dB,帧周期中将近一半的时间被用于感知,那么留给用户传输数据的时间就会很少.由图8可以看出,在-30 dB到-25 dB信噪比极低时,最优的用户密度基本不变,然后随着信噪比的增加,用户密度减小,说明好的信噪比需要较少的认知用户就能达到概率要求

4 小结

本文在考虑通知时间的情况下,建立了协作频谱感知吞吐量优化模型,联合优化用户密度和感知时间以使吞吐量最大,并作了理论分析和计算机仿真.通过仿真可以看到,受通知时间的影响,并不是认知用户数越多,吞吐量越大,而是存在一个最优值.因此,在研究分析协作感知系统的感知性能时,特别是参与感知的用户数较多时,考虑通知时间很有意义.

[1]Ghasemi A,Soura E S.Collaborative spectrum sensing in cognitive radio[C]//Baltimore：in Proc.IEEE DySPAN,Nov,2005：131-136.

[2]Liang Y C,Zeng Y,Peh E C Y,et al.Sensing throughput tradeoff for cognitive radio networks[C]//In Proc.IEEE Int.Conf.Commun.（ICC）,June,2006：5330-5335.

[3]Liang Y C,Zeng Y,Peh E C Y,et al.Sensing throughput tradeoff for cognitive radio networks[J].IEEE Trans.Wireless Commun, 2008,7（4）：1326-1337.

[4]Ganesan G,Li Y,Bing B,et al.Spatiotemporal sensing in cognitive radio networks[J].IEEE J.Sel.Areas Commun,2008,26（1）：5-12.

[5]Quan Z,Cui S G,Sayed A H.Optimal linear cooperation for spectrum sensing in cognitive radio networks[J].IEEE Journal of Selected Topics in Signal Processing,2008,2（1）：28-40.

[6]Ganesan G,Li Y.Copoperative spectrum sensing in cognitive radio[J].IEEE Trans.Wireless Commun,2007,6（6）：2204-2222.

[7]Peh E,Liang Y C.Optimization for cooperative sensing in cognitive radio networks[C]//Wireless Communications and Networking Conference,2007,WCNC 2007,IEEE：27-32.

[8]Peh E C Y,Liang Y C,Guan Y L,et al.Optimization of cooperative sensing in cognitive radio networks：A sensing throughput tradeoff view[J].IEEE Trans.Vehicular Technology,2009,58（9）：5294-5299.

（责任编辑：卢奇）

The throughput optimization based on user density and sensing time in cooperation cognitive networks

Cui Weiwei1,Du Juan2,Jia Xiaojian1
（1.Henan Institute of Science and Technology,Xinxiang 453003,China；2.Nanyang Institute of Technology,Nanyang 473000,China）

In cooperation cognitive network,the local sensing time is reduced by increasing the number of cognitive user for cooperation,but the reporting time is increased.So it's necessary to choose proper cognitive user number for cooperation to get the optimal perception performance.The optimization throughput model of cooperation cognitive network was established considering the reporting time.Under the premise of protection the primary users,the joint optimization of user density and sensing time maximize throughput.Simulation results showed that when the user density is large,the reporting time limits the improvement of throughput,select the appropriate number of concurrent users can make optimal throughput.

cognitive radio；cooperative spectrum sensing；throughput；optimization

TN925

A

：1008-7516（2015）01-0061-07

10.3969/j.issn.1008-7516.2015.01.014

2014-11-11

崔微微（1987—）,女,河南新乡人,硕士,助教.主要从事认知无线电频谱感知研究.