多孔钛材料的动态力学响应研究
2015-03-16任会兰宁建国
王 婧,任会兰,郝 莉,宁建国
(1北京理工大学 爆炸科学与技术国家重点实验室,北京 100081; 2北京建筑大学 理学院,北京 100044)
多孔钛材料的动态力学响应研究
王 婧1,任会兰1,郝 莉2,宁建国1
(1北京理工大学 爆炸科学与技术国家重点实验室,北京 100081; 2北京建筑大学 理学院,北京 100044)
通过一级轻气炮加载,对孔洞具有一定规律的多孔钛材料进行了平板撞击实验及数值研究。基于锰铜压阻计测量到的实验波形,获得了冲击波在多孔钛材料中传播的衰减效应以及冲击波波速和波后粒子速度的D-u冲击绝热关系。依照实验情况在非线性动力学有限元软件中建立了数值模型,并根据计算结果得到了冲击波的压力-时间波形以及冲击绝热关系,拟合出了多孔钛材料的多项式形式Grüneisen状态方程。通过对压缩度μ进行泰勒展开,结合冲击波基本关系式及冲击绝热关系,从理论上得到了多项式形式Grüneisen状态方程系数的具体表达式。
多孔钛材料;动态力学性能;Grüneisen状态方程
在针对多孔材料动态力学行为的研究中,研究范围可划分为两类:一类是在高压下,冲击波过后多孔材料中的孔隙被完全压实,材料进入密实状态;另一类则是在相对低的压力范围内,多孔材料并未被完全密实化。在对前者的研究中,Boade[1]在研究烧结多孔钨时利用爆轰驱动获得高压对多孔钨进行动态加载,测得的实验数据被证实与通过固体钨的Grüneisen参数预测出的多孔钨参数较为符合,同时证实了高压状态下多孔材料的各项冲击参数可根据其已知的基体材料的Hugoniout参数及Grüneisen参数来确定。而在第二类范围中,即研究多孔材料在较低压力范围内并未被完全压实的情况则相对复杂。由于多孔材料结构的复杂性,迄今为止,并没有合适的理论来解释多孔材料的波传播特性,而是借助经验公式来进行研究工作。经验公式是建立在获取大量实验数据的基础上,因此,对不同多孔材料的实验研究就显得尤为重要。
国内外大量学者对压力相对较低范围内的多孔金属材料动态力学性能作了相关实验研究,Bonnan等[2]通过平板撞击实验得到了低于2GPa压力下泡沫铝完整的应力波形和粒子速度波形,研究了压力-比容关系。Silva等[3]给出了孔隙未被完全压实这一压力区段中多孔铁的冲击性能,并讨论了实验研究中多孔铁的应变率相关性问题。在国内,李斌潮等[4]与王永刚等[5]分别通过落锤直接撞击实验和爆炸加载实验研究了较低压力段下泡沫铝中的冲击波传播以及衰减效应。
对于多孔金属动态力学性能的研究,实验手段多样化[6,7],如分离式Hopkinson压杆,轻气炮、直接高速撞击及爆炸实验等[8-10]。其中,用于平板撞击实验的轻气炮,作为产生平面应力波的基本工具获得了广泛的应用[11],可用来研究材料中波的传播特性以及冲击特性,同时能够基本满足不同初始压力段的实验需求。
多孔钛材料具有金属钛材料优异的力学特性,同时拥有传统多孔材料的衰减能力及防护能力,具有重要的研究价值。然而在国内外关于多孔钛的研究中,大多研究成果集中在制备方法上或是静态力学性能上[12-14],有关多孔钛动态力学性能的研究极少,尤其在研究规则孔洞的多孔钛方面。具有规则孔洞的多孔金属材料,可利用其特殊的孔洞结构,用于汽车轻量化结构、航空航天轻型构件、工业冲击减震结构等领域。然而对于蜂窝结构等传统的规则多孔金属材料,在受到动态载荷作用时,由于其孔壁较薄且孔洞附近会形成强应力集中,使得材料整体强度降低,无法承受较高的冲击载荷,造成该类材料的应用范围显著缩小[15]。以金属材料为基体,在基体上均匀排布通孔这一结构则可在维持传统规则孔洞材料优异性能的同时提高其动载荷承载能力,使得规则多孔金属材料能够更广泛地应用于工业工程中。本工作拟采用一级轻气炮对具有规则孔洞的多孔钛试件进行一维应变平面加载实验。由于实验测量技术的限制,本工作在利用轻气炮实验得到数据的基础上,对所采用的数值模拟方法进行验证。随后利用数值模拟的研究手段,对多孔钛的动态力学响应进行进一步的分析。
1 实验
1.1 实验材料与方法
样品选取工业纯钛作为基体材料,沿基体材料径向均匀分布三层孔洞,层与层之间呈90°分布,孔洞之间的间距相等(如图1所示),使得多孔钛试件的孔隙率基本达到30%,考虑到多孔试件的结构以及加工成本问题,试件中的孔洞均为直径1mm的圆形通孔。

图1 多孔钛试件照片Fig.1 The photograph of the cellular titanium sample
本研究中的靶板由基板、两层多孔钛试件、传感器、探针以及背板组成。基板和背板的材料与试件基体材料相同,传感器选用电阻为50Ω的双螺旋形锰铜压阻计。实验中,锰铜压阻计1放置于基板与试件中间,锰铜压阻计2放置于两片试件中间,锰铜压阻计3放置于试件与背板中间。压阻计都安装在试件的中心位置,使用聚酰胺包敷固定,避免因高压作用锰铜压阻计被提前剪断、导通。叠合好的试件组需放在平台上挤压以排空层与层之间的空气,放入60℃的恒温箱中烘干30min。随后将冷却充分的试件组用环氧树脂固化于基板底座,并用模具浇铸固化,即制成实验中所需靶板(如图2所示)。
气炮实验在中科院非线性力学国家重点实验室的一级轻气炮(内径101mm)上进行,实验装置如图3所示。气体室的高压气体推动飞片在炮管中高速运动并进入靶室对靶板进行平面撞击。置于不同位置处的锰铜压阻计负责测量该处的应力历史。应力波所携带的波源以及介质的力学特性信息将会通过传感器导出,通过波剖面的时间分析测量即可得到材料的动态特征信息。

图2 靶板照片 (a)靶板样品;(b)装配靶板Fig.2 Photographs of the target (a)target sample;(b)assembled target
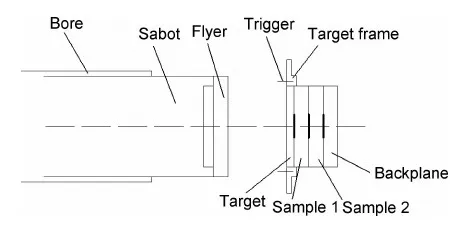
图3 轻气炮实验装置Fig.3 The gas gun device
气炮实验中的飞片出口速度决定了初始冲击波压力的大小。本研究中的实验采取了电测探针法获得飞片出口速度。飞片前端面先后触发两根间距为h的探针,通过触发探针所返回的时间信息可得到触发时间间隔t。飞片初速w即可通过w=h/t求得。另外,锰铜压阻计采集到的信号由示波器记录,该信号为反应压力的电压信号,可以通过标定公式将电压信号转为压力信号。由于在4~40GPa的压力范围内,电阻率与压力有线性关系,而在恒流电源供电下,电阻率可由电压标定,因此压力P可通过式(1)确定:
ΔV/V0=ΔR/R0=KpP
(1)
式中:ΔV为电压变化量;V0为初始电压;ΔR为传感器电阻的变化;R0为传感器初始电阻;Kp为已知的压阻系数。
为了保证实验中的靶板满足宽厚比大于2的要求以消除边侧稀疏波效应的影响,本实验中飞片的直径φ75mm,厚度6mm;靶板中基板以及背板的直径都为φ70mm,厚度分别为3,6mm。多孔钛材料试件的直径也为φ70mm,其余参数见表1。经计算可得宽厚比约为4.6,符合消除边侧稀疏波效应的宽厚比的要求。
1.2 结果与分析
本研究共进行4次轻气炮实验。飞片的打击速度在200m/s附近两组及100m/s附近两组,分别为表1中的T1,T2,T3,T4四个实验组。取T2组为典型实验组,实验中锰铜压阻计所获得的典型电压-时间曲线如图4所示,经过标定转换即可得到压力-时间曲线,如图5所示。

表1 多孔钛材料试样参数

图4 锰铜压阻计实测电压-时间信号Fig.4 The voltage and time curve measured by manganin gauge

图5 压力-时间曲线Fig.5 The pressure-time curve
由图5可明显看出,应力波在多孔钛试件中传播具有明显的衰减效应以及弥散效应。第一个测点所测得的波形显示了应力波在迅速上升至峰值后,并未出现率无关材料所具有的应力平台现象,而是随时间延长应力值迅速下降,体现了试件明显的衰减效应;在后续的测点中,波形不断被拉宽拉长,反映了试件材料的弥散效应。同时,由于试件材料中存在大量的孔洞,应力波传播至孔洞处,由于冲击载荷作用引起局部的拉伸以及剪切效应,导致孔洞变形甚至塌陷,从而引起材料结构的破坏,如图6所示。

图6 T1实验组冲击后的试件照片(a)多孔试件1;(b)多孔试件2Fig.6 Photos of the T1 cellular samples after impact(a)cellular sample 1;(b)cellular sample 2
图6中可以看到冲击后的试件中孔洞的变形。除去试件在回收仓碰撞所受到的损伤外,很显然试件中前几排孔洞的变形较为严重,而最后一排的孔洞基本保持未变形状态,体现了多孔试件的衰减特性,也说明了该试件具有一定的动态承载性能。
实验中飞片高速撞击靶板时,冲击波遵循质量守恒、动量守恒和能量守恒定律,其基本方程式为:
ρ0(D-u0)=ρ(D-u)
(2)
P-P0=ρ0(D-u0)(u-u0)
(3)
(4)
式中:ρ0,u0,P0,E0为初始状态参量;剩下五个待定参量分别为ρ,u,D,P,E。因此,实验只需测得其中任意两个量,便可求得其余所有参量,从而确定冲击压缩线上某一点的状态参数,并且通过同一初始状态下不同压力点上的参数值,即可获得与之相应的冲击压缩线的线段。
在试件中传播的冲击波波速D可直接测量。通过两个传感器所返回的波形起跳时间的差值即可得到冲击波在试件中传播的时间Δt。若试件长度为l,则冲击波波速D=l/Δt。
飞片材料的冲击压缩线已知[16]如式(5):
D-u0=5020+1.536(u-u0)
(5)
飞片以速度w冲击靶板,此时可根据式(3)可得:
Pf=ρf(-Df-w)(uf-w)
(6)
Pt=ρtDtut
(7)
并且对于飞片, 根据式(5)可得:
-Df-w=-5020+1.536(uf-w)
(8)
由此可得
Pf=ρf[-5020+1.536(uf-w)](uf-w)
(9)
同时,在碰撞接触瞬间,有边界条件:
Pf=Pt=P,uf=ut=u
(10)
联立(9),(10)两式即可求得靶内冲击波的粒子速度值u以及冲击波压力P。
至此,若代入初始状态参量,那么式(2)~(4)中所有的未知量都可以解出。
图7给出了四组实验中冲击波随时间在第一片试件和第二片试件中传播的位移-时间关系。显然,在不同的速度下,由两段直线的斜率,即冲击波分别在两个试件中的平均传播速度,都可看出冲击波在第二片试件中传播的速度较第一片试件中的波速有所下降;并且随着撞击速度的增加,两段直线的斜率都表现为增加,这表明了初始压力对冲击波速度的影响。初始压力越大,试件中的冲击波速度也越大。

图7 冲击波在试件中传播的位移-时间关系Fig.7 The distance-time curves of shock wave
多孔钛试件在受到强冲击载荷作用时具有明显的衰减特性,在上文中给出的典型压力-时间曲线中可以明显看出。第一个传感器所测得的压力峰值无法延续高压力平台,而是迅速下降,待冲击波传播至第二个及第三个传感器时,压力已大幅衰减,具体的衰减情况如图8所示。图8分别给出的是四组实验中三个测点传感器所测得的直观压力峰值随着时间的变化。首先,与冲击波波速的规律相同,对于飞片撞击速度越高的实验组,压力峰值表现越高。其次,应力波在第一个试件中传播时,其强度衰减非常迅速,以至传播至第二个传感器时,压力峰值的衰减值最高达到90%以上。该峰值-时间关系曲线与图6所示的实验结果一致。第二个传感器和第三个传感器所测得的压力峰值相差不大的原因在于冲击波在多孔钛材料中传播时,压力并非线性衰减,压力值到了某一范围后使得衰减幅度明显降低;同时,在峰值压力较小时,示波器通道之间的干扰信号也有可能影响实验测量结果的精确度。在以后的工作中,则可通过更加细致的实验技术提高测量结果的精度,获得更全面的数据。

图8 冲击波压力峰值-时间关系Fig.8 The P-t curves of shock wave
针对冲击波的实验研究以及测试技术而言,质点速度u以及冲击波波速D属于较容易测定的参量,而动态条件下的压力、比体积和比内能相对难以测量,因此在Hugoniot线的实验测定以及对材料高压状态方程的研究中,D-u形式的Hugoniot线最为常用。由于大量实验表明,在相当宽的实验压力范围内,D-uHugoniot线通常呈现出简单的线性关系式(11)。根据实验已经求得的数据点,可以拟合出关系式(12):
D=a0+λu
(11)
D=4376.83+1.342u
(12)
2 有限元模拟
在实验研究的基础上,采用非线性动力学有限元软件研究了多孔钛材料在平板撞击下的力学性能。由于实验存在成本高、信号不易捕捉等缺陷,采用数值模拟结合实验可以对多孔钛的力学性能进行进一步研究。
2.1 计算模型
图9给出了非线性动力学有限元软件中所使用的计算模型。计算模型完全依照实验中的真实尺寸进行建模(飞片直径φ75mm,厚度6mm;基板、试件以及背板的直径都为φ70mm,厚度分别为3,6,6mm,试件中孔洞大小为φ1mm, 排列模式按照图1所示),出于对称性及计算效率的考虑,取1/4模型进行计算。

图9 数值模拟1/4模型Fig.9 The 1/4 model of numerical simulation
飞片、基板、试件以及背板的材料均选取工业纯钛,材料模型选用双线性弹塑性模型。具体参数如表2所示。

表2 材料模型参数
在计算中,对飞片施加不同的初始速度,以期得到飞片撞击过程中试件上放置传感器所对应的单元的动力响应。
2.2 模型验证
由于实验中存在各种人工或天然误差,同时考虑到数值模拟中材料模型及参数的选取等问题,很难保证实验所得波形与数值模拟波形完全相同。因此,实验和数值模拟中重要参数一致即可说明数值模拟的合理性。
图10给出了在有限元软件中计算得到的压力-时间图与相应实验数据的对比。波形1,2,3分别为实验中三个传感器所测得的压力波形,波形1′,2′,3′分别为数值模拟中与实验传感器相应处单元所测得的波形,为了清楚直观便于研究,数值模拟结果的曲线中舍去了峰值压力之后的曲线。从图10可以看出,三个波形的起跳点都与实验波形的起跳点完全吻合,波形的形状趋势相差不大,峰值压力有一定误差。峰值压力以及波形的误差存在很多影响因素,包括应变片在试件上放置的位置,示波器通道之间的干扰以及试件测量误差等。在数值模拟的过程中,选取的应变片的位置很难保证与实验中的位置完全相同,示波器不同通道之间的相互干扰容易影响到实验中低应力区的测量结果,试件的加工尺寸和设计尺寸存在一定误差也会导致实验结果与模拟结果的误差。由于本工作在对方程(2)~(4)中的未知量求解时主要依据的是波形起跳点差值,因此认为数值模拟所给出的结果在进行类似的计算时是合理的。
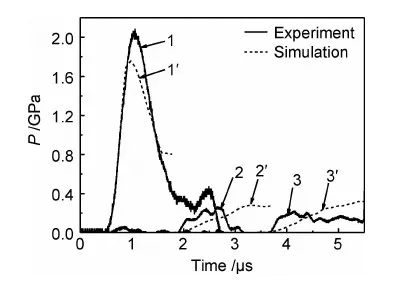
图10 数值模拟与实验结果的对比Fig.10 The comparison between results of numerical simulation and experiment
2.3D-u冲击绝热线
除了对四组实验分别进行了相应的数值模拟计算,还增加了飞片撞击速度分别为125,150,300,400m/s四个计算组。通过计算结果可以拟合出D-u形式的Hugoniot线为:
D′=4257.49+1.333u′
(13)
并在图11中绘制出以上曲线。在图11中对比实验结果式(12)和数值模拟结果式(13)可发现,D-u关系中的常数a0,数值模拟与实验的误差为2.727%;常数λ的误差则为0.671%,均属于合理的范围内。
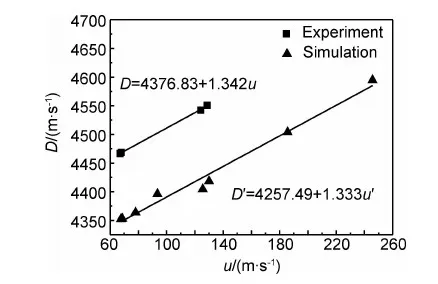
图11 D -u形式的Hugoniot线Fig.11 TheD -uHugoniot curves
3 多项式形式Grüneisen状态方程
Grüneisen状态方程广泛应用于高压下固体中的冲击波研究,在忽略材料畸变的情况下,可以用形式较为简单的多项式Grüneisen方程来描述材料的容变部分。方程的具体形式为:
P=C1μ+C2μ2+C3μ3
(14)
其中μ为材料的压缩度,定义为:
(15)
式中:ρ为材料的现实密度;ρ0为材料的初始密度。
根据数值模拟所得的八组实验结果,联立式(2)以及式(14),(15),可以得出曲线如图12所示。

图12 多项式Grüneisen EOS拟合曲线Fig.12 The fitting curve of polynomial Grüneisen EOS
拟合得出曲线的具体表达式为:
P=58.53μ+74.74μ2+795.54μ3
(16)
将通过实验计算得到的数据点放入图12中与拟合曲线进行对比,可以发现四个实验数据点与曲线吻合较好。
从图12中可以看出,在100~400m/s之间的飞片速度撞击条件下,压缩度μ的变化范围从0.015~0.06,可将其看作小量。由于(λ-1)μ也是小量且有0<(λ-1)<1。对其进行泰勒展开,则有:
(17)
u=a0μ[1+(λ-1)μ+(λ-1)2μ2+…]
(18)
式(18)联立式(10)及式(3),可得:
(19)
将式(18)与式(13)对照,略去式(18)中μ3以后的各高阶项,则可得多项式形式Grüneisen状态方程中各项的系数:
(20)
将多孔钛的D-u形式的Hugoniot线式(12)代入式(19)后,有
P=57.1μ+95.13μ2+57.01μ3
(21)
将式(21)与式(15)进行对比,发现前两项符合较好,尤其是系数C1,而系数C3差距较大。因为在针对小量μ进行展开时,舍去了后面高阶项。并且文中的压缩度μ变化范围小,在这个小范围内,P-μ关系近乎为线性,因此式(20)中C1值起到决定性作用。在较高压力区使用式(17),(18)直接推导材料的多项式形式Grüneisen状态方程时,应注意在系数C3处增加修正因子,以减小误差。
4 结论
(1)对孔洞具有一定规律的多孔钛材料进行了一维应变下的动态力学性能实验研究,得到了冲击波波速及峰值压力随时间衰减的关系,并给出了该材料的D-u冲击绝热线。
(2)通过对数值模拟和实验结果进行比较,验证了与实验相对应的数值模拟所得结果的可靠性,并且得到了相应的冲击绝热关系,给出了多孔钛的多项式形式Grüneisen状态方程。
(3)结合冲击波基本关系式及冲击绝热关系,对压缩度μ进行泰勒展开,得到了多项式形式Grüneisen状态方程各项系数的具体表达式。
[1]BOADERR.Dynamiccompressionofporoustugsten[J].JournalofAppliedPhysics, 1969, 40(9): 3781-3785.
[2]BONNANS,HEREILPL.Experimentalcharacterizationofquasistaticandshockwavebehaviorofporousaluminum[J].JournalofAppliedPhysics, 2008, 83(11):5741-5749.
[3]DaSILVAMG,RAMESHKT.Therate-dependentdeformationsofporouspureiron[J].InternationalJournalofPlasticity, 1997, 13(6-7): 587-610.
[4] 李斌潮,赵桂平, 卢天健. 高孔隙率闭孔泡沫铝的低应变率压缩行为[J]. 力学学报,2011,43(1):122-135.
LIBin-chao,ZHAOGui-ping,LUTian-jian.Lowstrainratecompressivebehaviorofhighporosityclosed-cellaluminumfoams[J].ChineseJournalofTheoreticalandAppliedMechanics, 2011,43(1):122-135.
[5] 王永刚,胡时胜,王礼立. 爆炸荷载下泡沫铝材料中冲击波衰减特性的实验和数值模拟研究[J]. 爆炸与冲击, 2003, 23(6): 516-522.
WANGYong-gang,HUShi-sheng,WANGLi-li.Shockattenuationinaluminumfoamsunderexplosionloading[J].ExplosionandShockWaves, 2003,23(6):516-522.
[6] 经福谦. 实验物态方程导引[M]. 北京: 科学出版社, 1999.
[7] 王礼立. 应力波基础[M]. 北京:国防工业出版社,2010.
[8] 刘海燕, 宋卫东, 宁建国. 不同晶粒度钨合金动态力学性能研究[J]. 材料工程, 2007,(6): 3-6.
LIUHai-yan,SONGWei-dong,NINGJian-guo.Dynamicbehavioroftungstenalloyswithdifferentgrainsizes[J].JournalofMaterialsEngineering, 2007,(6): 3-6.
[9] 姜芳, 陈涛, 宁建国. 钢筋混凝土在冲击载荷下的动态力学性能[J]. 材料工程, 2009, (3): 45-48.
JIANGFang,CHENTao,NINGJian-guo.Dynamicmechanicalpropertiesofreinforcedconcretesubjectedtoshockloading[J].JournalofMaterialsEngineering, 2009, (3): 45-48.
[10]FIELDJE,WALLEYSM,PROUDWG,etal.Reviewofexperimentaltechniquesforhighratedeformationandshockstudies[J].InternationalJournalofImpactEngineering, 2004, 30(7): 725-775.
[11] 赵士达, 沈乐天, 赵双录. 用于材料动态性能实验的单极轻气炮[J]. 兵工学报,1985,(4):49-55.
ZHAOShi-da,SHENLe-tian,ZHAOShuang-lu.Asingle-stagelightgasgunforimpactstudies[J].ActaArmamentarii, 1985,(4):49-55.
[12] 李伯琼. 多孔钛的孔隙特征和力学性能的研究[D]. 大连:大连交通大学, 2005.
LIBo-qiong.TheinvestigationofporecharacteristicandmechanicalpropertyofporousTi[D].Dalian:DalianJiaotongUniversity,2005.
[13] 张晓伟,王彦莉,陈利,等. 多孔金属介质的力学性能及其参数依赖性研究[J]. 材料工程, 2014, (2): 55-59.
ZHANGXiao-wei,WANGYan-li,CHENLi,etal.Mechanicalpropertiesofporousmetalmaterialsandtheirdependenceongeometricparameters[J].JournalofMaterialsEngineering, 2014,(2): 55-59.
[14] 刘培生,夏凤金,罗军. 多孔材料模型分析[J]. 材料工程, 2009, (7): 83-87.
LIUPei-sheng,XIAFeng-jin,LUOJun.Analysesoftheclassicalmodelforporousmaterials[J].JournalofMaterialsEngineering, 2009, (7): 83-87.
[15]IDET,TANEM,IKEDAT.Compressivepropertiesoflotus-typeporousstainlesssteel[J].JournalofMaterialsResearch, 2006, 21(1): 185-193.
[16]STEINBERGDJ.EquationofStateandStrengthPropertiesofSelectedMaterials[M].Livermore:LawrenceLivermoreNationalLaboratory, 2003.
Dynamic Mechanical Response of Cellular Titanium Material
WANG Jing1,REN Hui-lan1,HAO Li2,NING Jian-guo1
(1 State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology,Beijing 100081,China; 2 School of Sciences,Beijing University of Civil Engineering and Architecture,Beijing 100044,China)
Shock properties of cellular titanium with regular pores were investigated by one-stage gas gun plate impact technique. With the experimental curves caught by the manganin gauge, the attenuation effect of shock wave propagating through the cellular titanium samples and the adiabatic impactD-urelationshipbetweenshockwavevelocityandthepracticalvelocityaftershockwaveareobtained.Accordingtotheexperiments,anumericalmodelisbuiltinnonlineardynamicfiniteelementsoftware.Thepressure-timecurvesofshockwaveandtheadiabaticrelationareobtainedfromthenumericalresults,andthepolynomialGrüneisenequationofstateofcellulartitaniumisgivenbynumericalsimulation.Moreover,withTaylorexpansionofthesqueezingdegreeμ,thecoefficientofthepolynomialGrüneisenequationisdeducedbyusingshockwaverelationsandtheadiabaticrelation.
cellular titanium material;dynamic mechanical property;Grüneisen equation of state
10.11868/j.issn.1001-4381.2015.09.014
TB34
A
1001-4381(2015)09-0087-07
教育部高等学校博士学科点专项科研基金资助项目(201311 01110013);国家自然科学基金资助项目(11172045)
2014-06-13;
2015-03-27
郝莉(1963-),女,博士,教授,现主要从事爆炸力学研究,联系地址:北京建筑大学大兴校区永源路15号(102612),E-mail:haoli_haoli@126.com
