复数在坐标正反算计算中的应用
2015-03-16杨伟星
杨伟星
(中国电建集团西北勘测设计研究院有限公司,西安 710065)
文章编号:1006—2610(2015)03—0015—03
复数在坐标正反算计算中的应用
杨伟星
(中国电建集团西北勘测设计研究院有限公司,西安 710065)
通过引进复数对测量中坐标方位角计算进行公式推导、分析研究、合理优化相关数据验证,得出了计算坐标方位角简便公式。优化CASIO编程计算器编程程序,避免在测量中计算方位角繁琐的象限判断条件,从而提高测量中的工作效率。
复数;象限;坐标方位角;坐标正反算;CASIO编程计算器
鉴于复数运算的诸多优点,本文主要通过对复数的模和复角的几何意义的应用,引进到坐标方位角计算中。使得坐标正反算变得简单化,方便CASIO编程计算器编程,提高了工作效率。
1 数学笛卡尔坐标系复平面与测量高斯平面直角坐标系复平面
数学笛卡尔坐标系与测量高斯平面坐标系复数表示法关系如图1。
复数的表达形式有直角坐标、极坐标和指数形式3种表达方式[1-2]。其中直角坐标系和极坐标系也称复数的几何表达,CASIO编程计算器只能对前两种复数表达形式进行计算。
z=x+yi=r∠θ=reiθr>0
(1)
式中:r∠θ是复数的极坐标表示形式;r是复式z的模Abs(absolute);θ是复数z的复角Arg(argument)。
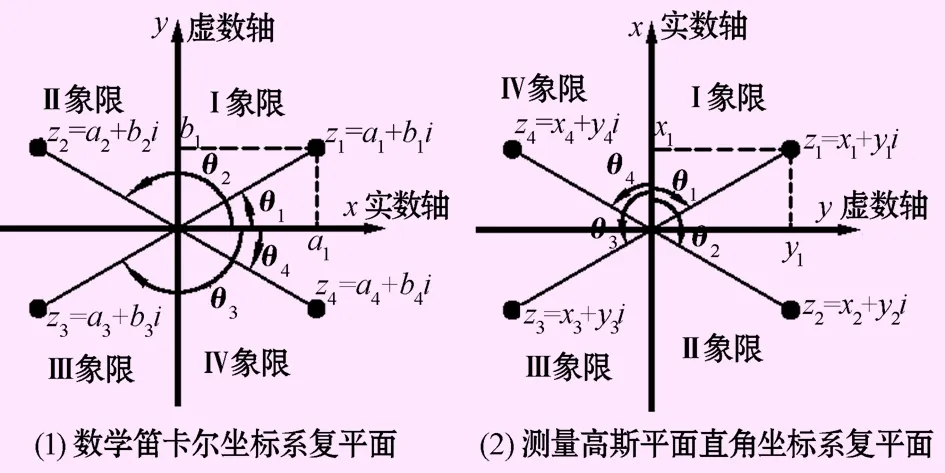
图1 数学笛卡尔坐标复平面与测量高斯平面坐标系复平面表达法关系示意图
在图1(1)中所示数学笛卡尔坐标系中,当z点位于Ⅰ、Ⅱ象限时方向角θ取逆时针,此时0° ≤θ≤180°;当z点位于Ⅲ、Ⅳ象限时方向角θ取顺时针,此时0° ≤θ≤-180°。
在图1(2)中所示测量高斯平面直角坐标系中,当z点位于Ⅰ、Ⅱ象限时方向角θ取顺时针,此时0°≤θ≤180°;当z点位于Ⅲ、Ⅳ象限时方向角θ取逆时针,此时0°≤θ≤ -180°。
由数学坐标复平面和测量坐标系复平面之间关系可知,计算坐标方位角时完全可以借助复数的模和复角进行求解。两点之间距离r=Abs(z)即复数的模,两点之间方位角α=Arg(z),θ≥0时则α=θ,θ≤0时则α=θ+360°。
2 坐标正反算推导原理
坐标正算是通过坐标方位角和距离求待求点的坐标,坐标反算通过已知2点的坐标计算2点之间距离和方位角[3-4]。
测量高斯平面坐标系与测量高斯平面坐标系复平面表达关系如图2。
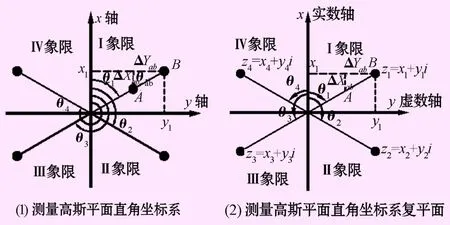
图2 测量高斯平面直角坐标系与复平面坐标系表示法示意图
2.1 测量高斯平面直角坐标系下坐标正反算公式推导
2.1.1 坐标正算
已知点A(xa,ya),两点之间距离Sab、方位角θab,求B(xb,yb),由图2(1)可得到:
Δxab=Sabcosθab=xb-xa
(2)
Δyab=Sabsinθab=yb-ya
(3)
因此可得:
xb=xa+Sabcosθab
(4)
yb=ya+Sabsinθab
(5)
式(4)、(5)即在测量高斯平面坐标系下坐标正算公式[3,5]。
2.1.2 坐标反算
已知A(xa,ya)、B(xb,yb)两点坐标,求AB两点之间的距离Sab、方位角θab。由图2(1)可知:
(6)
(7)
式(6)、(7)即为坐标反算公式。由于公式中坐标方位角的计算是两点之间的反正切值,因此,需要进行象限条件判断,具体求法有多种,下面给出一种通用求法。
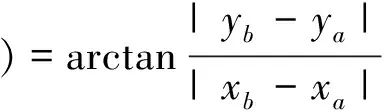
(8)
当xb-xa>0且yb-ya≥0,则Ⅰ象限,此时方位角θab=θab(锐角);
当xb-xa<0且yb-ya≥0,则Ⅱ象限,此时方位角θab=180°-θab(锐角);
当xb-xa<0且yb-ya<0,则Ⅲ象限,此时方位角θab=180°+θab(锐角);
当xb-xa>0且yb-ya<0,则Ⅳ象限,此时方位角θab=360°-θab(锐角);
当xb-xa=0且yb-ya>0,此时方位角θab=90°;
当xb-xa=0且yb-ya<0,此时方位角θab=270°。
2.2 测量高斯平面直角坐标系复平面下坐标正反算公式推导
2.2.1 坐标正算
在测量高斯平面直角坐标系复平面下,已知点A(xa,yai),A、B之间距离rab(复数模)、方位角θab(当复角θab>0即为方位角,当复角θab<0时方位角360°-θab)。由复数性质及图2(2)则有:
zb=za+rab∠θab=xa+yai+rab∠θab
(9)
式(9)即为测量高斯坐标系复平面下的坐标正算公式。
2.2.2 坐标反算
在测量高斯平面直角坐标系复平面下,已知点A(xa,yai)、B(xb,yb),求A、B两点之间距离rab(复数模)、方位角θab,由复数性质及图2(2)知:
za=xa+yai=ra∠θa
(10)
zb=xb+ybi=rb∠θb
(11)
zab=xab+yabi=(xb-xa)+(yb-ya)i=rab∠θab
(12)
式中:rab为复数的模;θab为复角,当复角θab>0时方位角为θab,当复角θab<0时方位角为360°+θab。
式(12)为在测量高斯平面直角坐标系复平面下的坐标反算公式。
3 2种坐标正反算的分析比较
坐标正反算在工程测量中有着极其重要作用,通过坐标正反算公式的优化可以提高现场工作人员的工作效率。下面就以测量高斯平面直角坐标系与复平面系下坐标正反算的计算流程进行分析。
3.1 测量高斯平面直角坐标系与复平面系坐标的正算流程
测量高斯平面坐标系与复平面系坐标正算流程如图3。
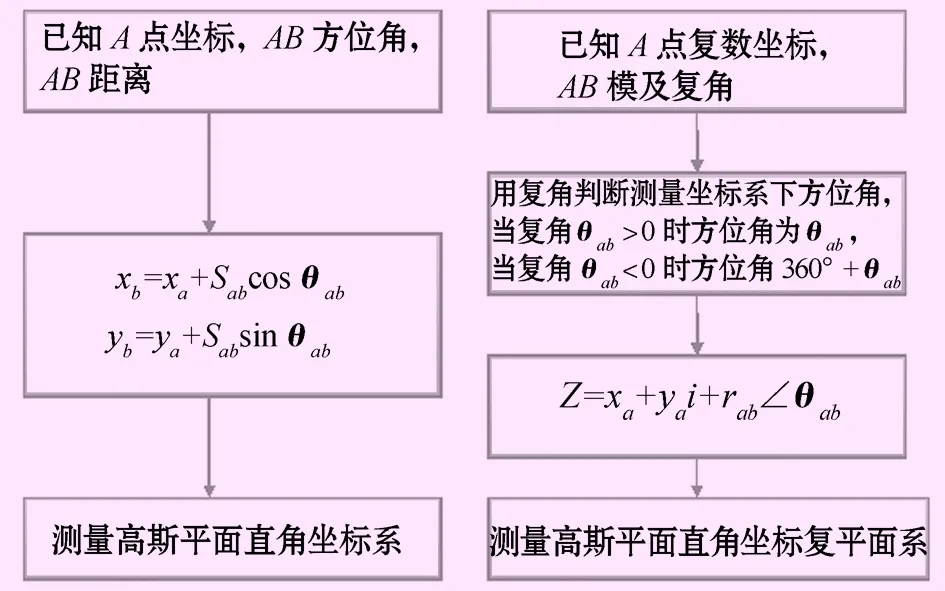
图3测量高斯平面坐标系与复平面系下坐标正算流程图
由图3可知,复平面系下将坐标正算公式用一个复数形式表达,较测量高斯平面直角系下用2个公式形式表达简化。
3.2 测量高斯平面直角坐标系与复平面系坐标的反算流程
测量高斯平面坐标系与复平面系坐标反算流程如图4、5。
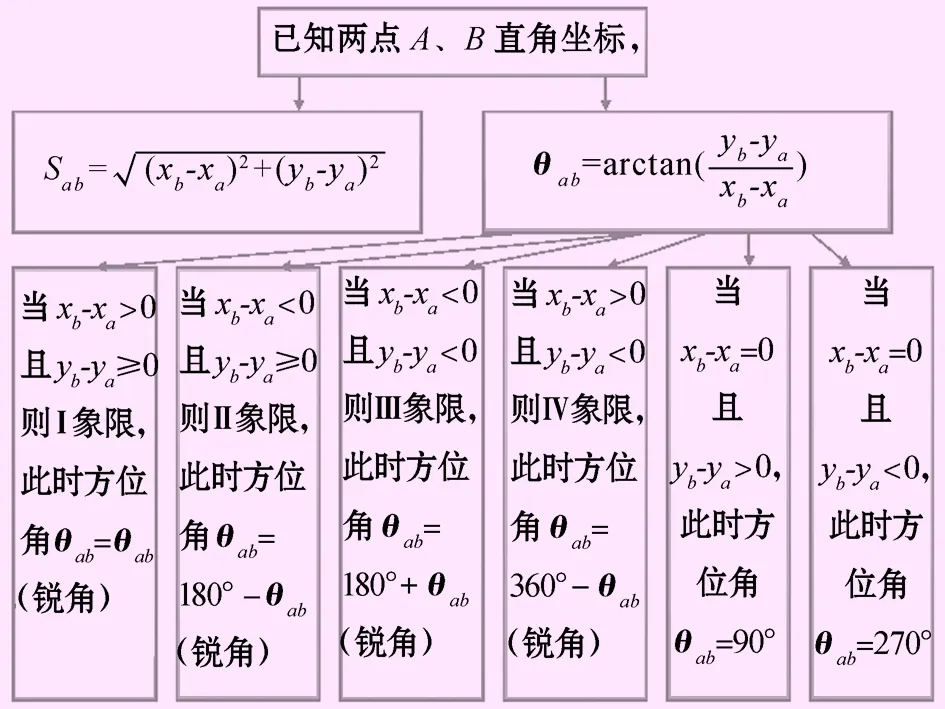
图4 测量高斯平面坐标系下坐标反算流程图
由图4、5可知,在引入复数进行坐标反算时可以大大简化计算公式,计算可以起到事半功倍作用。
3.3 复数在坐标正反算CASIO编程中的应用
某工程测量中公路直线两端点复数坐标M(A,Bi)、N(C,Di),两点之间距离T,方位角F。以CASIO-4800P编程计算器为例,对MN两点进行坐标正反算编程。程序如下:
LBIA:{A,B}:Z=0=>Goto 1:≠>Goto2 坐标正反算判断条件,
LBI 1:{C,D}:Pol(C-A,(D-B)i):S=I◢F=J◢J<0=>F=J+360°◢ 坐标正算,
GotoA:LBI 2:{S,F}:Rec(S,F):C=A+Ii◢D=B+Ji◢GotoA坐标反算。
由上面的程序可知:编程计算器对坐标正反算进行程序编写时,通过引入复数,使得程序变得简洁、明了,提高了工作效率。
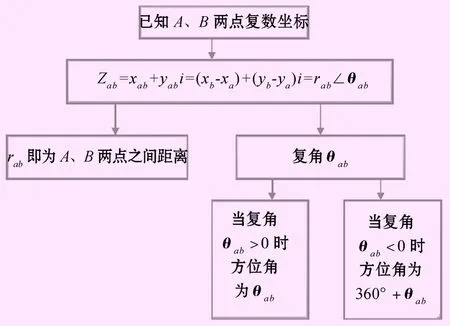
图5 测量高斯平面坐标系复平面下坐标反算流程图
4 结 语
在测量中通过引进复数求解坐标正反算可以得到以下结论:① 坐标正算中使公式变得更加简单化,方便CASIO编程计算器编程。② 坐标反算中尤其是方位角计算中大大减少了方位角象限的判断,为工程测量中CASIO编程提供便利。
[1] 覃辉.CASIOfx-5800P编程计算器公路与铁路施工测量程序转换[M].上海:同济大学出版社,2009.
[2] 刘启寿,魏兰花. 坐标转换在悬高测量中的应用[J].西北水电,2012,(01):24-25,33.
[3] 孔祥元,郭际明,刘宗全.大地测量学基础[M].武汉:武汉大学出版社,2001.
[4] 覃辉.fx-50P编程计算器原理与测量程序[M].北京:人民交通出版社,2008.
[5] 杨伟星,张建生,张堃.引水隧洞中圆弧段纵断面处模板的优化设计与精度分析[J].南水北调与水利科技,2010,(4):35-37.
[6] 宁津生,刘经南,陈俊勇.现代大地测量理论与技术[M].武汉:武汉大学出版社,2006.
Application of Complex Number in Coordinate Positive and Negative Calculation
YANG Wei-xing
(POWERCHINA Xibei Engineering Corporation Limited, Xi'an 710065,China)
By application of complex number, calculation of the coordinate azimuth in survey is verified by formula calculation, analysis, study and optimized relevant data. Therefore, a simplified formula for calculation of coordinate azimuth is derived. Program of the CASIO programming calculator is optimized, avoiding the complicated conditions of quadrant judgment for azimuth calculation in survey and improving the survey efficiency.
complex number; quadrant; coordinate azimuth; coordinate positive and negative calculation; CASIO programming calculator
2014-08-15
杨伟星(1979- ),男,河南省平顶山人,助理工程师,硕士,从事电站的质量控制与变形观测工作.
TP391
A
10.3969/j.issn.1006-2610.2015.03.005
