基于人工神经网络模型的地下水水位动态变化模拟
2015-03-16魏光辉
魏光辉
(新疆农业大学水利与土木工程学院,乌鲁木齐 830052)
文章编号:1006—2610(2015)03—0006—04
基于人工神经网络模型的地下水水位动态变化模拟
魏光辉
(新疆农业大学水利与土木工程学院,乌鲁木齐 830052)
地下水水位的预测在流域地表水和地下水资源的综合规划管理中起着非常重要的作用。在该研究中,人工神经网络模型被应用于希尼尔水库周边地下水水位的预测中。采用研究区6口地下水观测井资料,用人工神经网络模型进行模拟预测1周后的地下水水位。模型输入因子包括此前1周蒸发量、水库水位、排渠水位、抽水量和观测井地下水位,因此模型有15个输入节点和6个输出节点。将3种不同的神经网络训练算法,即自适应学习速率动量梯度下降反向传播算法(GDX)、LM算法和贝叶斯正则化算法(BR)用于地下水水位预测,并对模拟结果进行了评估。结果表明:3种神经网络训练算法在研究区地下水水位预测中表现均较好。然而,BR算法的性能总体略优于GDX和LM算法。将BR算法训练的人工神经网络模型用于预测研究区未来2、3和4周的地下水水位,虽然地下水位预测的准确性随着时间的增加有所降低,但模拟效果仍然较好。
人工神经网络;地下水位预测;GDX算法;LM算法;BR算法
0 前 言
地下水是一种宝贵的自然资源,并已成为世界上所有气候区域的可依赖水源[1]。在发展中国家,由于地下水可直接输送到贫困区、更具成本效益以迅速便捷程度超过地表水,故开发地下水已成为一种扶贫的工具[2]。然而,由于地下水资源的过度开发,加上越来越多的地下水污染,导致地下水水位下降和含水层枯竭,这严重威胁了供水和生态系统的可持续性。许多非可持续利用地下水的后果日趋明显,世界各地,特别是在发展中国家,都在关注如何从含水层获得一个长期的可持续地下水量[1,3-5]。因此,水资源的可持续管理特别是地下水资源的可持续管理是目前及今后一个时期需要亟待解决的问题。
目前,地下水建模已成为一种强大的工具来帮助水资源管理者,优化地下水的使用,进而保护这一重要资源。在过去的几年中,基于数值模型的物理方法被应用于地下水系统的模拟和分析。随着计算机技术的广泛使用,这种方法正在被越来越多的水文地质工作者和环保工作者所使用,并且已经将应用范围从地下水含水层的安全产量分析扩展到地下水污染整治等问题。在大多数发展中国家,由于资料匮乏,使用基于物理方法的数值模型受到很大限制。因此,在这种情况下,经验模型成为一个有吸引力的模型——因为它们可以提供较为有用的结果,且具有所需资料较少的特点。人工神经网络(ANN)模型就是此类模型中的一种,它非常适合于非线性动态系统建模[6],且不需要对物理性质进行明确的定性和定量,并能解决大规模的复杂问题[7]。目前它已用于降雨径流模型,降水预报、河流流量建模、蒸散量建模、水质和地下水建模等[6,8-9]。与地表水水文研究相比,人工神经网络在地下水水文学中的应用数量相对较少。在地下水水文学中,神经网络技术已用于含水层参数估计[10-12],地下水水质预测[13-14],地下水水位预测[15-17]。以往关于地下水水位预测的研究中,人工神经网络模型主要用于单井预测,即使用1组输入参数预测地下水水位。然而,在目前研究中,通过使用人工神经网络模型来同时预测井群的地下水水位已成为当务之急。本文将人工神经网络模型与自适应学习速率动量梯度下降反向传播算法(GDX)、L-M算法和贝叶斯正则化算法(BR)相结合,用于希尼尔水库周边地区地下水井群水位预测,这对于新疆的地下水开发利用具有极其重要的参考价值。
1 研究区概况
希尼尔水库位于新疆库尔勒市境内,地理坐标介于86°13′~86°18′E,41°33′~41°38′N。水库从孔雀河第一分水枢纽引水,是经库塔干渠总干渠输水的注入式大(2)型平原水库。由于水库蓄水,势必将导致周边地下水位在一定程度上的上升。鉴于此,希尼尔水库在2000年建设之初,就在周边区域布设了地下水观测井,进行周边区域的地下水水位观测。
本文以希尼尔水库下游的库尔勒市西尼尔村为研究区,对研究区的观测井地下水位进行分析预测。研究区一共布置了6口地下水位观测井,观测井位置示意见图1。研究区农业灌溉用水主要来自于地下水,并有少量地表水作为补充灌溉。目前该区域共有12口井用来灌溉,这些井的建设及管理由当地的用水户协会统一负责。
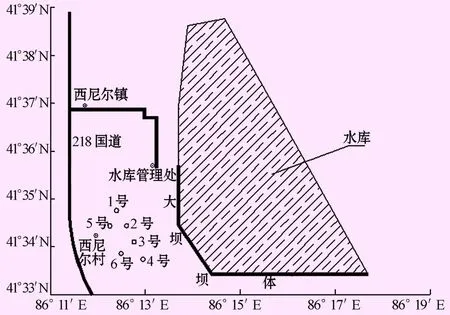
图1 希尼尔水库及观测井位置示意图
2 材料与方法
2.1 数据来源
本研究的数据来源来自希尼尔水库2005年1—12月共计52组观测井水位资料及同期的气象(降水、蒸发)、水库水位、排渠水位等资料。
2.2 神经网络算法概述
人工神经网络是一个并行分布式信息处理系统[18],类似于人脑中的生物神经网络。本文采用前馈式神经网络结构结合自适应学习速率动量梯度下降反向传播算法(GDX)、LM算法和贝叶斯正则化算法(BR)进行模拟效果比较[19],以确定合适的算法来进行研究区地下水水位预测。
2.2.1 前馈神经网络
在前馈神经网络中,节点一般都安排在层上,从第1个输入层开始,并在最后1个输出层结束。它可以有几个隐藏层,每1层又有1个或多个节点(BP神经网络结构见图2)。信息从输入层传递到输出端。第1层的节点将连接到下一层,但不是在一层。因此,输出层的每一个节点只依赖于上一个输入层节点及对应的权值。前馈神经网络的主要优势是易掌握,可以逼近任意输入、输出层[20]。
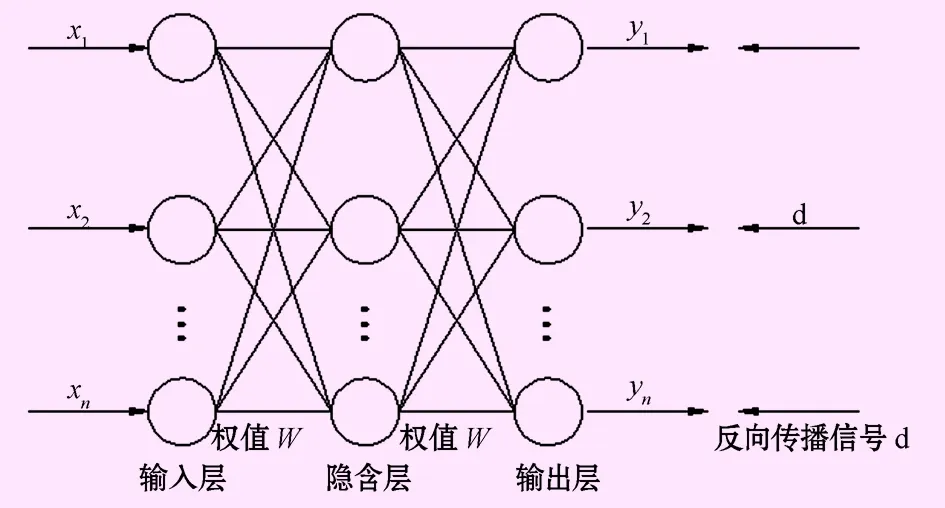
图2 BP神经网络结构图
2.2.2 训练算法
(1) 自适应学习速率动量梯度下降反向传播算法(GDX)
在标准BP算法中,算法结果对于学习速率的设置非常敏感[21-22]。为了克服这个问题,GDX算法结合自适应学习率与动量训练。自适应学习率试图保持尽可能大的学习步长,同时保持学习的稳定。每个变量根据动量梯度下降进行调整。这就像一个低通滤波器,动量允许网络忽略错误表面的小功能。该训练算法是最简单、最常见的训练算法[23-24]。
(2) L-M算法
传统的BP算法在进行网络训练时,往往会陷入某个局部最小点。L-M算法使每次迭代不再沿着单一的负梯度方向,而是允许误差在梯度下降法和高斯-牛顿法之间自适应调整网络权值,使网络有效收敛,大大提高了网速的收敛速度和泛化能力[25]。
L-M优化算法权值调整公式[26]:
x(i+1)=xi-[JTJ+μI]-1JTe
(1)
式中:x为神经网络权值;J为误差对权值微分的雅可比矩阵;μ为控制学习过程的一个标量;e为残余误差向量。当标量μ为零时,就成为牛顿法;当标量μ增加时,等式就成为小步长梯度下降法。由于牛顿法具有运算速度更快、更准确、更接近误差最小值的特点。
(3) 贝叶斯正则化算法
贝叶斯正则化算法涉及优化的目标函数,它包括传统的平方和误差函数以及一个称为“管理者(regularizer)”的函数。贝叶斯正则化算法能够使最优权值衰减参数在训练期间自动进行调整[27]。
2.3 BP神经网络设计
在Matlab R2011a中,BP神经网络设计包括网络的生成、训练及仿真可以通过调用一系列函数来实现[28-29]。
由于水库周边地下水水位变化规律具有明显的周期特征。因此,对该时间序列进行模拟时,采用前i个点值来得到第i+1个点值的方法。通过自相关分析,达到显著水平(a=0.05)的本周地下水埋深与前一周的地下水埋深有关。同时,通过相关分析选取了前一周水库平均水位、平均蒸发量、排渠水位与抽水量作为模型输入节点(即输入因子)。因此,模型输入节点共计15个,输出节点为6个(6口观测井的地下水位)。
2.4 评价标准
本文采用相关系数(R)、平均偏差(bbias)、均方根误差(RRMSE)与纳什效率(Nash-Sutcliffe efficiency,EN-S)来评价模型计算结果,各评价指标计算式如下[30]:
(2)
(3)
(4)
(5)

3 结果与讨论
3.1 人工神经网络训练算法评价
在人工神经网络模型进行预测前,先要对模型进行训练。本模型输入节点共计15个,输出节点为6个(6口观测井),以该模型来预测研究区下一周的地下水水位。各种算法模型最优隐含神经元个数的计算结果见表1。
由表1可以看出,各种算法模型最优隐含神经元个数中,L-M算法所需隐含神经元个数最少,为20个,BR算法所需隐含神经元个数最多,为40个。
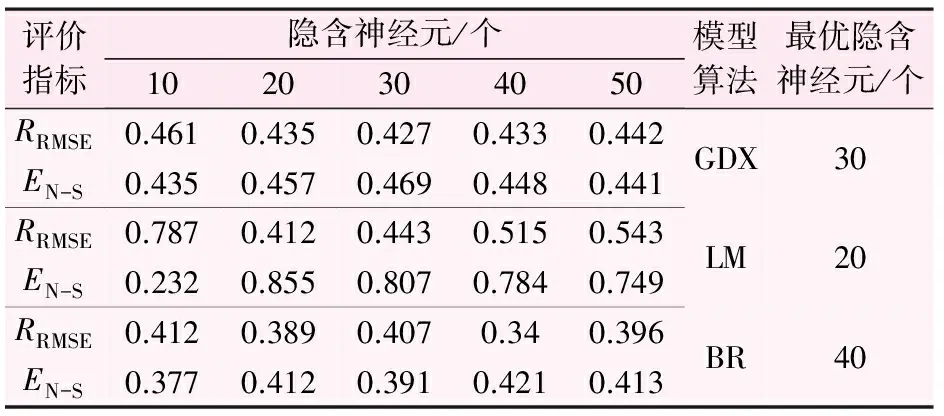
表1 模型隐含神经元个数计算表
根据希尼尔水库管理处提供的2005年1月—2005年12月共计52组观测井水位资料及同期的气象(降水、蒸发)、水库水位、排渠水位等资料,通过神经网络模拟训练,得到1周后研究区地下水位不同算法下的评价指标值(见表2)。
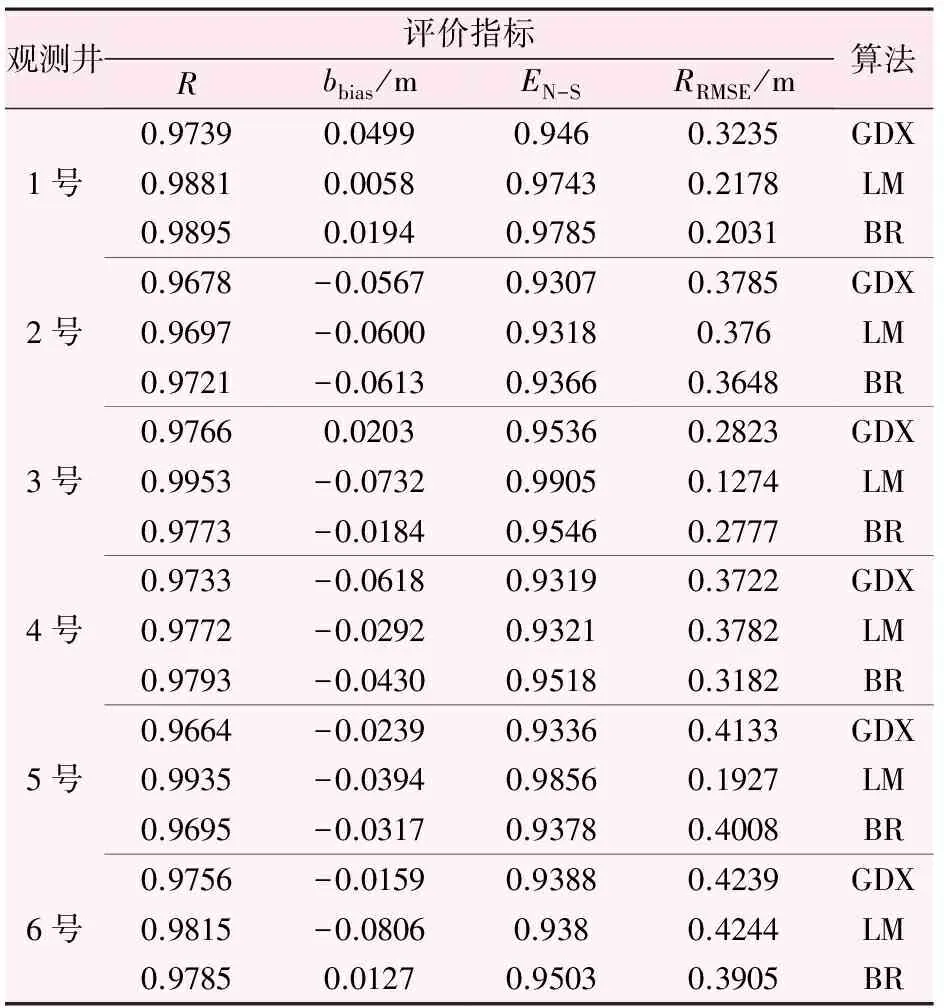
表2 不同算法下的评价指标值对比表
由表2可以看出,不同算法模型各项评价指标计算值相差不大,但以BR算法略优于GDX算法与LM算法。
3.2 研究区地下水位的预测
本文选取研究区前一周水库平均水位、平均蒸发量、排渠水位与抽水量作为模型输入节点(即输入因子),利用BR算法,对未来2、3、4周的地下水位进行预测分析。因此,模型输入节点仍然为15个,输出节点为6个(6口观测井)。
考虑到篇幅所限,本文以1号井与5号井为例,利用评价指标对模型预测值进行评价(见表3)。
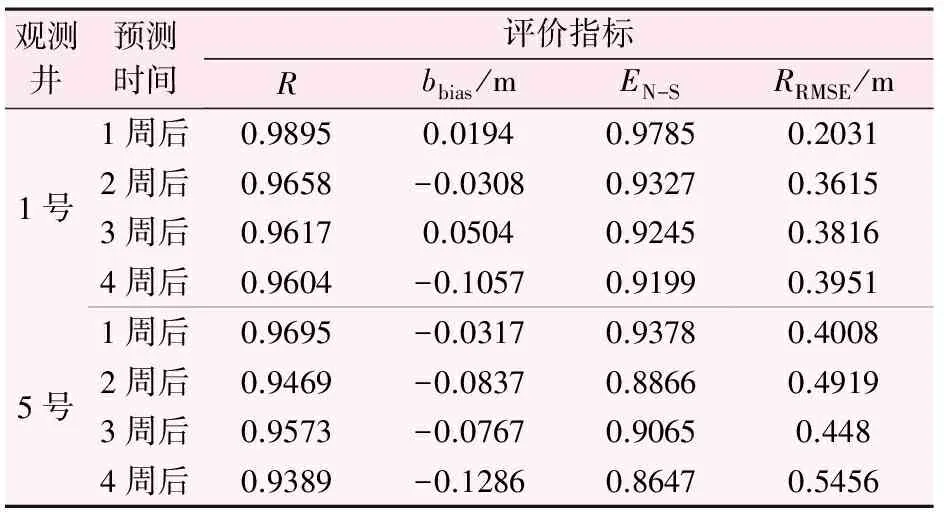
表3 不同预测时间段模型拟合效果评价表
由表3可以看:① 随着预测时间的推移,模型预测精度有降低的趋势;② 尽管模型预测精度有所降低,但是其精度仍然满足实际需要,具有可信性。
综上所述,经过算法改进的人工神经网络模型可用于研究区1、2、3与4周之后的地下水位预测。因此,将人工神经网络技术应用于水文或水文地质参数资料缺乏地区是可行的。
4 结 语
本文将3种神经网络算法模型用于研究区的地下水水位预报中,采用前馈神经网络结构模拟了研究区6口观测井1周后的地下水水位。网络模型的输入因子为此前1周蒸发量,水库水位,排渠水位,抽水量和观测井地下水位,共有15个输入节点和6个输出节点。使用4项统计指标对3种网络训练算法进行评估。结果表明:3种训练算法产生的结果近似相同,可用这3种算法中的任意一种来对研究区的地下水水位预测。然而,根据本文的统计指标,BR算法略优于其它2种算法。采用基于BR算法训练的人工神经网络模型进一步对研究区未来2、3、4周的地下水水位进行预测。结果发现,随着预测时间的推移,模型预测精度有降低的趋势,但是其精度仍然满足实际需要,具有可信性。总体而言,尽管本研究中所使用的数据有限,但是经过算法改进的人工神经网络模型仍然能够合理地预测研究区未来1周地下水位甚至更远时间(未来2、3、4周)的地下水水位。
[1] Todd DK, Mays LW. Groundwater hydrology[C].Wiley, Hoboken,2005.
[2] IWMI.The strategic plan for IWMI 2000-2005[M].International Water Management Institute(IWMI),Colombo,2005:28.
[3] Alley WM.The journey from safe yield to sustainability[J].Ground Water,2004, 42(1):12-16.
[4] 许国志.系统科学[M].上海:上海科技出版社,2003.
[5] 胡铁松,袁鹏,丁晶.人工神经网络在水文水资源中的应用[J].水科学进展,1995,6(1):76-82.
[6] 张弘强,王春红.基于MATLAB的BP神经网络进行教师评估[J].哈尔滨师范大学自然科学学报,2005,21(5):43-46.
[7] 韩力群.人工神经网络理论、设计及应用[M].北京:化学工业出版社,2002.
[8] 刘国东,丁晶.运用BP网络预测地下水位[J].西安地质学院学报,1997,19(2):52-57.
[9] ASCE Task Committee. Artificial neural networks in hydrology-II: hydrologic applications[J].J Hydrol Eng ASCE,2000, 5(2):124-137.
[10] Garcia LA, Shigdi A. Using neural networks for parameter estimation in ground water[J].J Hydrol,2006, 318(1-4):215-231.
[11] Samani M, Gohari-Moghadam M. A simple neural network model for the determination of aquifer parameters[J].J Hydrol,2007,340:1-11.
[12] Karahan H, Ayvaz MT.Simultaneous parameter identification of a heterogeneous aquifer system using artificial neural networks[J].Hydrogeol J,2008, 16:817-827.
[13] Hong YS, Rosen MR. Intelligent characterization and diagnosis of the groundwater quality in an urban fractured-rock aquifer using an artificial neural network[J].Urban Water,2001,3(3):193-204.
[14] Kuo V, Liu C. Evaluation of the ability of an artificial neural network model to assess the variation of groundwater quality in an area of black foot disease in Taiwan[J].Water Res,2004,38(1):148-158.
[15] Uddameri V.Using statistical and artificial neural network models to forecast potentiometric levels at a deep well in South Texas[J].Environ Geol,2007,51:885-895.
[16] Krishna B, Rao YRS, Vijaya T. Modeling groundwater levels in an urban coastal aquifer using artificial neural networks[J].Hydrol Process,2008, 22:1180-1188.
[17] Banerjee P, Prasad RK, Singh VS. Forecasting of groundwater level in hard rock region using artificial neural network[J].Environ Geol,2009, 58:1239-1246.
[18] 陈玉芳.BP神经网络的算法改进及应用研究[D].成都:电子科技大学,2004.12-14.
[19] 杨旭,冯国章.基于BP网络的中长期水文预报精度影响分析[J].东北水利水电,2003,21(2):1-3.
[20] 邱林,陈晓楠.基于模拟退火算法的BP网络在水文水资源中应用[J].华北水利水电学院学报,2005,26(1):123.
[21] 储诚山,张宏伟.基于遗传算法和BP神经网络的用水量预测[J].中国农村水利水电,2006,(4):36-38.
[22] Hagen MT, Demceth HB, Beale MN. Neural network design[M].PWS,Boston,1996.
[23] Bishop CM .Neural networks for pattern recognition[M].Oxford University Press,New York,1995.
[24] Mackay DJC.Apractical Bayesian framework for back-propagation networks[J].Neural Comput,1991,4(3):448-472.
[25] 张兵,袁寿其.基于L-M优化算法的BP神经网络的作物需水量预测模型[J].农业工程学报,2004,20(6):73-76.
[26] Daliakopoulos IN, Coulibaly P.Groundwater level forecasting using artificial neural network[J].J Hydrol,2005,309:229-240.
[27] Bishop CM.Neural networks for pattern recognition[M].Oxford University Press, New York,1995.
[28] 魏铁军,王永成.BP网络在三江平原井灌区地下水埋深预测中的应用[J].黑龙江水专学报,2009,36(1):26-30.
[29] 魏光辉. 基于RBF神经网络的河川年径流量预测[J].西北水电,2014,(05):14-17.
[30] 邓丽娟. 新疆车尔臣河流域近50余年来主要水文要素变化研究[D].乌鲁木齐:新疆农业大学,2012.
Dynamic Variation Simulation of Ground Water Table Based on Artificial Neural Network Model
WEI Guang-hui
(College of Hydraulic and Civil Engineering, Xinjiang Agricultural University, Urumqi 830052,China)
Predication of the ground water table plays an important role in planning management of catchement surface and ground water resources. In this study, the artificial neural network model is applied in predication of the ground water table around the Xinier reservoir. By application of data from 6 monitoring wells in the study area and of the artificial neural network model, the ground water table after one week is predicated by simulation. The factors input the model include evaporation, reservoir level, escape canal level, water pumped volume and ground water table of the monitoring wells in last week. Therefore, the model is with 15 input points and 6 output points. Three different neural network methods of GDX, LM and BR methods are applied for the predication of the ground water table. The study shows that all three methods perform well in the predication. Generally, BR performance is better than these of GDX and LM. The artificial neural network model trained by BR method is applied for the predication of the ground water table in future 2nd, 3rd and 4th weeks in the study area. The simulation results are still better although the accuracy of the predication of the ground water table slightly decreases with time increment.
artificial neural network model; predication of ground water table; GDX method; LM method; BR method
2014-12-21
魏光辉(1981- ),男,新疆石河子人,高级工程师,主要从事干旱区水资源利用与工程建设管理.
新疆水文学及水资源重点学科资助(XJSWSZYZDXK2010-12-02).
P641.2
A
10.3969/j.issn.1006-2610.2015.03.002
